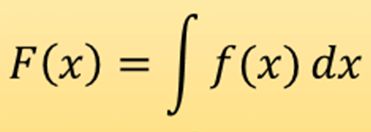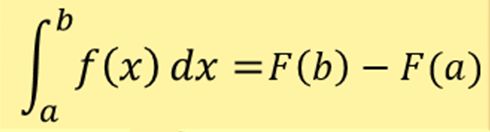☆☆☆数学の基礎概念☆☆☆
微分と積分
－微分と積分－
１．導関数
２つ以上の値を持つことのできる文字を変数、変数の動く範囲を変域と呼ぶ。いま、ｘにその変域の値を自由に与えた時、それに応じてｙの値が決まるなら、
ｘを独立変数、ｙを従属変数、または、ｘを単に変数、ｙをその関数と呼ぶ。
変数ｘにある値を与えた時、関数ｙの値がただ１つだけ決まるなら１価関数、ｎ個決まるならｎ価関数、無限に決まるなら無限多価関数という。１価関数以外を多価関数という。
また、関数は、陽関数、陰関数、逆関数、遇関数、奇関数、合成関数、増加関数、減少関数、単調関数、代数関数、超越関数などの呼び名で区別されることもある。
独立変数の変域は関数の定義域とも呼び、その時、従属変数のとり得る値の全体を値域という。
さらに、不等式ａ≦ｘ≦ｂを満たすｘの範囲は、ａ，ｂを両端に持つ閉区間であり、［ａ，ｂ］と表示する。
ａ＜ｘ＜ｂの場合は、開区間であり、（ａ，ｂ）で表示する。少なくともａ，ｂの一方が－∞または∞の時は無限区間であり、ａ，ｂが共に有限の時は有限区間という。
また、ａ≦ｘ＜ｂ、ａ＜ｘ≦ｂの場合、［ａ，ｂ），（ａ，ｂ］と表示する。
変数ｘがｘ1からｘ1＋Δｘまで変化すると、その関数ｙ＝ｆ(ｘ)は、ｆ(ｘ1)からｆ(ｘ1＋Δｘ)まで変化する。
いま、Δｙ＝ｆ(ｘ1＋Δｘ)－ｆ(ｘ1)とすれば、Δｘを変数の増分、Δｙを関数の増分という。この時、増分の比は、平均変化率と呼ばれ、
となる。
関数ｙ＝ｆ(ｘ)がｘ＝ａを含む区間で定義され、ａとａ＋Δｘの間における平均変化率Δｙ／ΔｘがΔｘ→０の時、有限の極限が存在すれば、
これをｆ(ｘ)のａにおける微分係数、微係数または変化率と呼び、
で表示する。ある区間の各点で微分係数が存在すれば、ｘの関数と考えられ、ｆ(ｘ)のｘについての導関数と呼び、ｆ'(ｘ)で表示される。
すなわち、微分係数が存在すれば、関数はその点において微分可能、存在しなければ、微分不能という。
また、関数の微分係数または導関数を求めることを微分するという。
なお、ｆ(ｘ)のｘについての導関数は、簡単に次のように表示することもある。
dｙ／dｘ，ｆ'，ｙ'，Ｄｆ(ｘ)
２．極限値
数列｛ａn｝において、ｎが限りなく大きくなる時、ａnが一定の値αに限りなく近づくならば、この数列はαに収束するという。また、αはこの数列の極限または極限値という。
この場合、次のように表記される。
ａn→α(ｎ→∞)
ｎ→∞の時、ａn→α
数学的には、「どんなに小さい正数εが与えられても、εによって決まる十分に大きな番号ｎ0が存在して、ｎ0より大きなすべてのｎについて、∣ａn－α∣＜εが成立する。」と定義される。
なお、ｎ→∞の時、ａn→∞(ａn→－∞)ならば、数列は正(負)の無限大に発散するという。収束もせずに、無限大に発散もしない場合、数列は振動するという。
最も基本的な数列の収束性の判定法は、その有界性と単調性を示すことにある。
数列ａnが上に有界とは、任意のｎに対して、ａn≦αなる定数αが存在することであり、下に有界とは、ａn≧βなる定数βが存在することである。
αを数列の一つの上界、βを一つの下界という。上にも下にも有界であれば、単に有界という。
極限値問題１(数列の極限値)
極限値問題２(級数の極限値)
極限値問題３(関数の極限値)
３．微分公式
一般公式（ｕ，ｖ，ｗ，・・・はｘの関数、ａは定数）
基礎微分公式（ｍ，ａは定数）
４．高次導関数と高次微分
関数ｙ＝ｆ(ｘ)の導関数ｙ'＝ｆ'(ｘ)がｘについて微分可能ならば、その導関数を第２次導関数と呼び、
と表示する。これから、数学的帰納法によって、第ｎ次導関数が定義できる。
第２次以上の導関数は、
ｙ"，ｙ'''，ｙ(4)，ｙ(5)，・・・，ｙ(n)，・・・
と表示され、これを高次導関数という。
５．全微分と偏微分
変数が２つの関数ｚ＝ｆ(x,y)の微分を考える。この時、ｚ0＝ｆ(x0,y0)として、ｘ，ｙ，ｚの増分をそれぞれ、
dｘ＝ｘ＋ｘ0
dｙ＝ｙ＋ｙ0
dｚ＝ｚ＋ｚ0
とする時、
dｚ＝ｆx(x,y)dｘ＋ｆy(x,y)dｙ
をｚの全微分という。
全微分の意味は、点ｘ，ｙを中心に、ｘ方向にΔｘ進み、ｙ方向にΔｙ進んだ時の関数ｆ(x,y)の変化量Δｚ、
Δｚ＝ｆx(x,y)Δｘ＋ｆy(x,y)Δｙ
を考え、その極限を示している。
いま、関数ｚ＝ｆ(x,y)のｙを一定値と考えれば、関数ｚ＝ｆ(x,y)はｘだけの関数になる。
この時、関数ｚ＝ｆ(x,y)の微係数として、
が存在する。この関数の極限値は、関数ｚ＝ｆ(x,y)のｘについての偏導関数(偏微分係数)となり、ｆ'x(x,y)＝∂ｆ／∂ｘと表示する。
同様に、関数ｚ＝ｆ(x,y)のｘを一定値と考えれば、関数ｚ＝ｆ(x,y)はｙだけの関数になり、関数ｚ＝ｆ(x,y)のｙについての偏導関数(偏微分係数)ｆ'y(x,y)＝∂ｆ／∂ｙが存在する。
(全微分と偏微分の具体的な事例)
関数ｚ＝ｘｙ2－２ｘ2＋３ｙを考える。この時、ｘ，ｙの偏微分は、
ｆ'x(x,y)＝ｙ2－４ｘ
ｆ'y(x,y)＝２ｘｙ＋３
となる。したがって、関数ｚ＝ｆ(x,y)の全微分は、
dｚ＝(ｙ2－４ｘ)dｘ＋(２ｘｙ＋３)dｙ
となる。
６．不定積分
関数Ｆ(x)の導関数Ｆ'(x)が関数ｆ(x)に等しいならば、Ｆ(x)はｆ(x)の原始関数と呼ばれる。この時、Ｆ(x)はｆ(x)の１つの不定積分となる。
また、Ｃを１つの定数とすれば、Ｆ(x)＋Ｃも１つの不定積分となる。
Ｆ'(x)＝ｆ(x)
{Ｆ(x)＋Ｃ}'＝Ｆ'(x)＝ｆ(x)
一般に、関数ｆ(x)の不定積分は、次のように表示され、Ｃは積分定数と呼ばれている。また、ｆ(x)の不定積分を求めることを積分するという。
 |
ｆ(x)dｘ＝Ｆ(x)＋Ｃ |
(不定積分の基本公式)
|
ｘndｘ |
＝ |
|
＋Ｃ (ｎ≠－１) |
|
ｅxdｘ＝ｅx＋Ｃ |
|
ａxdｘ |
＝ |
|
＋Ｃ (ａ＞０，ａ≠１) |
|
sinｘ dｘ＝－cosｘ＋Ｃ |
|
cosｘ dｘ＝sinｘ＋Ｃ |
(不定積分の簡単な解法事例)
(参考)置換積分法
|
(ａｘ＋ｂ)ndｘ |
(ａ≠０) |
|
(不定積分の関係式)
|
ａｆ(x)dｘ＝ａ |
|
ｆ(x)dｘ |
(但し、ａは定数) |
|
{ｆ(x)＋ｇ(x)}dｘ＝ |
|
ｆ(x)dｘ＋ |
|
ｇ(x)dｘ |
|
{ｆ(x)－ｇ(x)}dｘ＝ |
|
ｆ(x)dｘ－ |
|
ｇ(x)dｘ |
(不定積分の具体的事例)
|
(ｘ3＋ｘ2)dｘ |
| ＝ |
|
ｘ3dｘ＋ |
|
ｘ2dｘ＝ |
(１／４)ｘ4＋(１／３)ｘ3＋Ｃ |
(但し、Ｃは積分定数) |
|
(４ｘ3＋６ｘ2)dｘ＝４ |
|
ｘ3dｘ＋６ |
|
ｘ3dｘ＝ |
６(１／３)ｘ3＋４(１／４)ｘ4＝ |
ｘ4＋２ｘ3＋Ｃ |
(但し、Ｃは積分定数) |
７．定積分
不定積分は，関数f(x) に対して，微分すると関数f(x) になる 関数であった。定積分は，不定積分に積分区間の両端の値を代入した値の差である。
(不定積分と定積分の違い)
(不定積分)
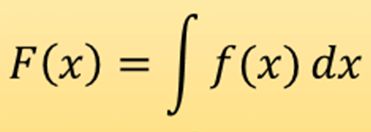
微分したらｆ(ｘ)になる関数をもとめる。
(定積分)
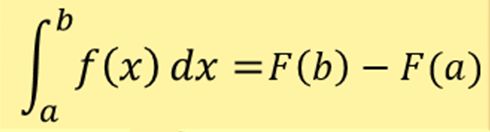
ｆ(ｘ)をａからｂまで積分して値の差(面積)を求める。
|
(定積分の具体的事例)
 |
(２ｘ3＋１)dｘ |
| ＝ |
 |
(１／２)ｘ4＋ｘ |
 |
 |
＝ |
(１／２)･３4＋３)－(１／２)･２4＋２)＝ |
８７／２－１０＝ |
６７／２ |
(放物線と直線で囲まれた面積)
 |
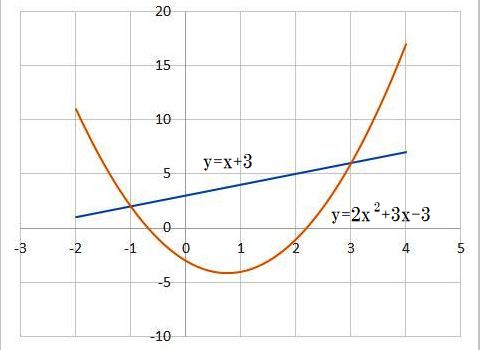
{(ｘ＋３)－(２ｘ2＋３ｘ－３)}dｘ |
| ＝ |
|
{－(２／３)ｘ3－ｘ2＋６ｘ} |
|
 |
| ＝ |
－(２／３)･３3－３2＋６･３＋(２／３)･１－１－６)＝ |
１８＋２／３－４＝ |
６４／３ |
(参考・面積問題「１／６公式」)
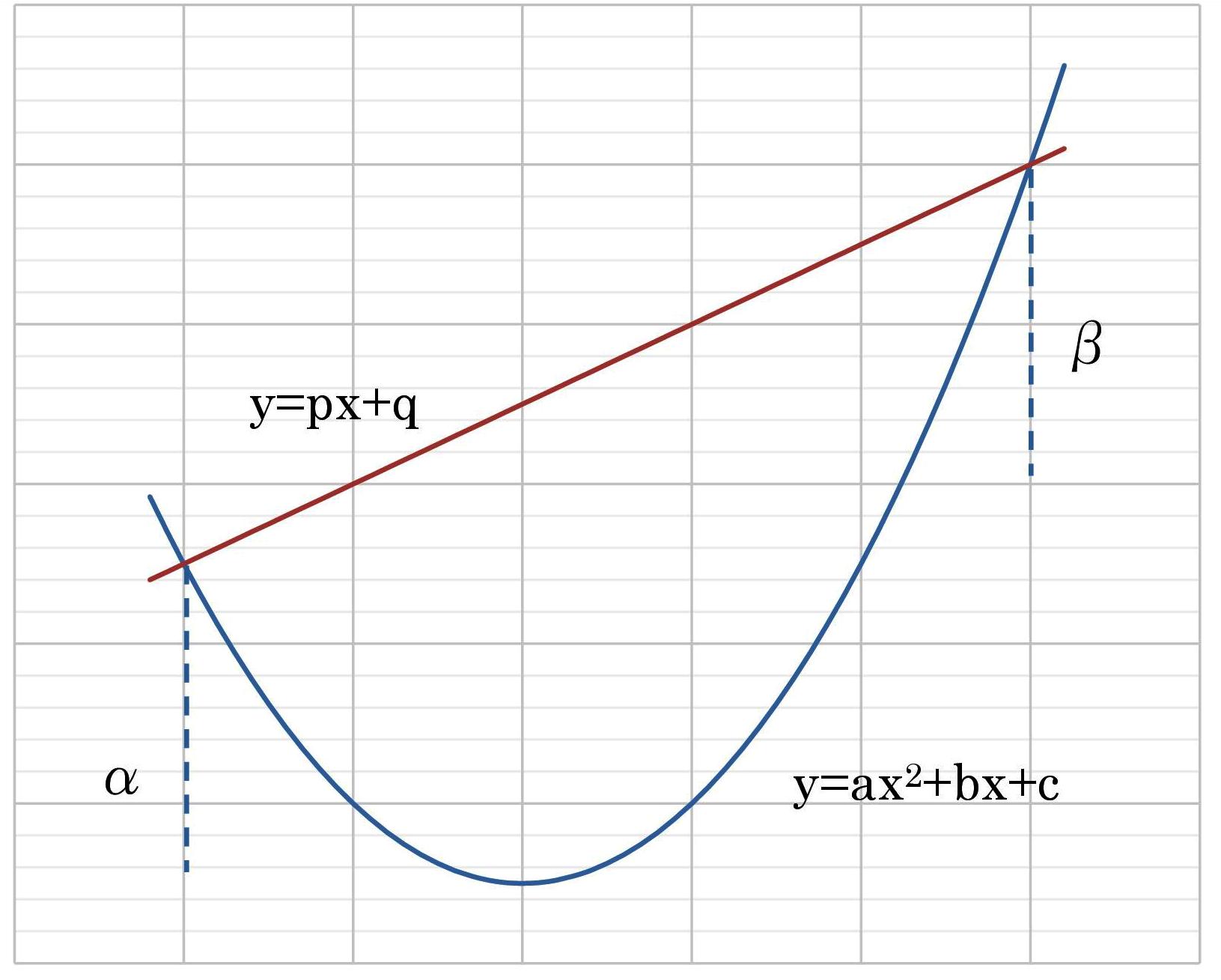Ｓ＝(|ａ|／６)(β－α)3
-証明-
|
 |
ａ(ｘ－α)(ｘ－β)dｘ |
| ＝ａ |
|
|
(ｘ－α){(ｘ－α)＋(α－β)}dｘ |
| ＝ａ |
|
|
{(ｘ－α)2＋(α－β)(ｘ－α)}dｘ |
| ＝|ａ| |
|
(ｘ－ａ)3／３－(β－α)(ｘ－α)2／２ |
|
|
|
以上
（２０１３年３月２４日）
戻る
|