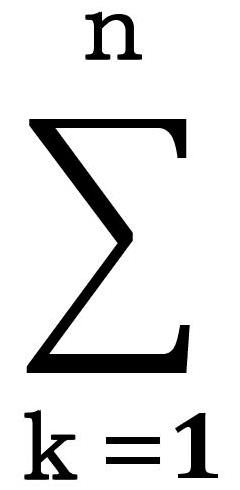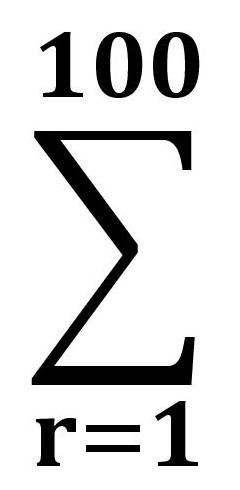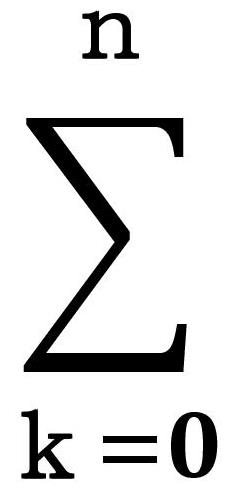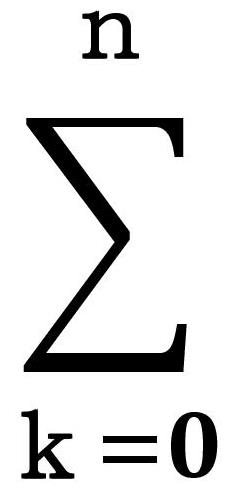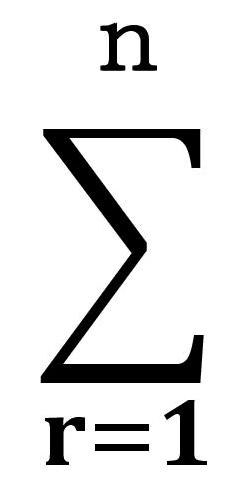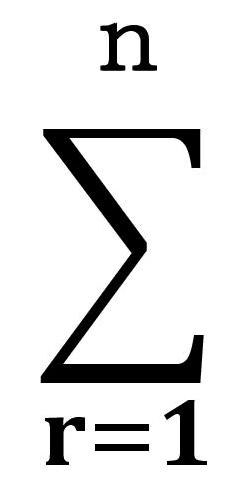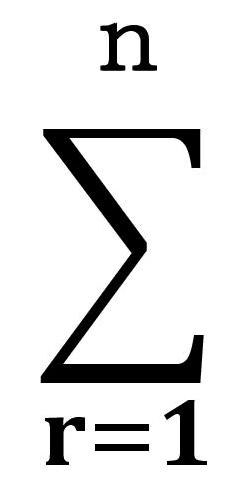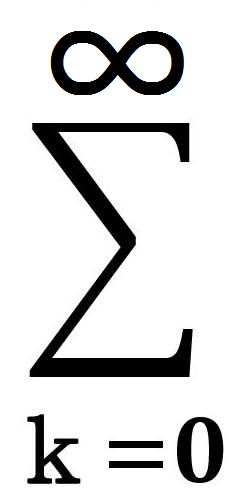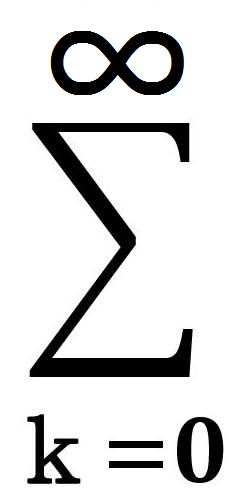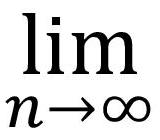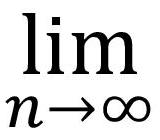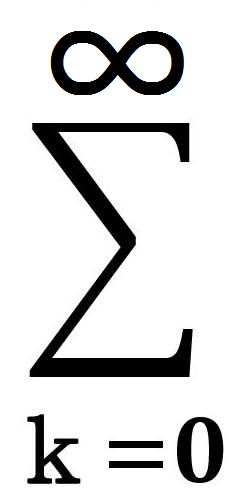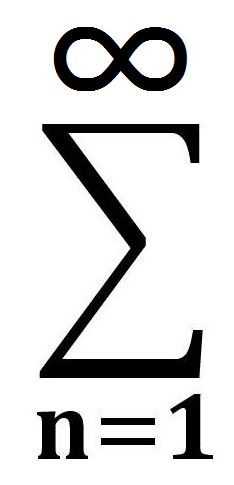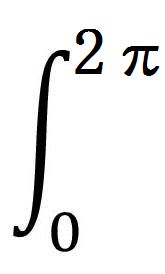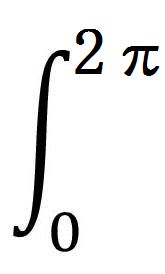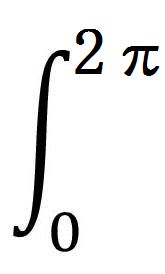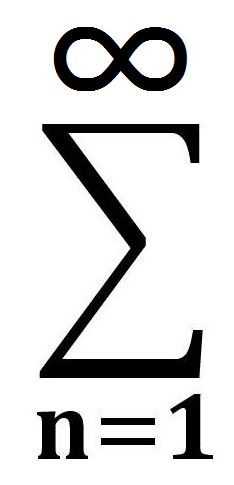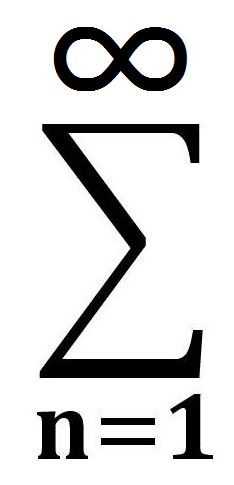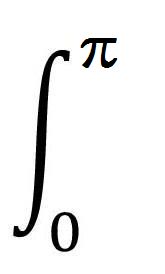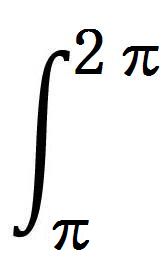☆☆☆数学の基礎概念☆☆☆
☆☆☆数学の基礎概念☆☆☆
数列と級数

-数列と級数-
1.数列と級数
数列とは、a1,a2,a3,・・・の形のもので、aはある一定の規則に従って並んでいる数のことである。ここで、数anは、この数列の一般項といわれている。
数列は、有限個の項を持つか、無限個の項を持つかにより、有限数列と無限数列に区別される。数列が作られる規則は、計算すべき項の個数を表す、文字nを用いて、計算の規則が表示される。
例えば、自然数も数列であり、奇数や偶数も数列である。次の公式は、代表的な数列の事例である。
公式1.
an=1/n (n=1,2,3,・・・)
数列:1,1/2,1/3,1/4,1/5,・・・,1/2n,・・・
公式2.
an=1/2n (n=1,2,3,・・・)
数列:1/2,1/4,1/8,1/16,・・・,1/n,・・・
公式3.
an=1+2n (n=1,2,3,・・・)
数列:3,5,7,9,11,・・・,1+2n,・・・
いま、実数rのn個の積を指数表記し、rnを一般項と見て、r1,r2,r3,・・・,rnと並べる。これは指数nを添字とする一つの数列である。
ここで、指数nはべき数とも呼ばれ、実数rは基数あるいは底と呼ばれている。この時、数列の項の数はn個、nは項の番号でもある。
さて、1<rならば、rn<rn+1、すなわち、
r1<r2<r3<r4<・・・<rn
が成立する。これは増加数列と呼ばれる。この数列は、どの二項を取っても値が単純に増加して行く。したがって、単調数列ともいう。
また、0<r<1ならば、nが大きくなるに従って、積rnは減少する。この時、不等号の向きは逆向きrn>rn+1となる。よって数列は、
r1>r2>r3>r4>・・・>rn
が成立する。これは減少数列と呼ばれる。この数列は、nの増大と共に各項の値は0に近づく。したがって、これも単調数列である。
次に、定数rの無限個の積を考える。これは無限数列である。
|
|
rn= | r×r×r×r×r×・・・ |
| |
 |
| |
無限個 |
項の番号nを限りなく大きくすると、第n項の大きさは、
① 1<rの時、限りなく大きくなる。
② r=1の時、1。
③ r<1の時、0に限りなく近づく。
④ r≦-1の時、どのような値にも近づかない。
となる。
一般に、無限数列anにおいて、項の番号nを限りなく大きくすると、
・ anがある有限な値αに近づくならば、極限値αに収束するという。
・ anが次第に大きくなるならば、正の無限大に発散する。
・ また、-anの場合は、負の無限大に発散する。
・ これらのどちらでもないならば、極限は存在しない。あるいは発散するという。
さらに、収束する2つの数列を考えた場合、
この四則計算の規則は、
が成立する。ただし、bn≠0,β≠0である。
2.級数展開
級数とは、数列の項を形式的に+の記号で結んだもので、数列a1,a2,a3,・・・から、
a1+a2+a3+・・・+an+・・・
を得る。級数は、総和記号Σを用いて略記できる。
無限に多くの項の形式的な和は無限級数と呼ばれる。級数がn個の項しか持っていない場合は有限級数となる。
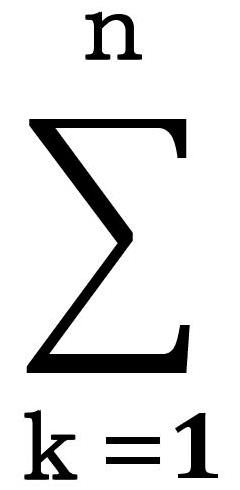 |
ak=a1+a2+a3+・・・+an |
典型的な事例として、自然数を1から100までの合計を考える。
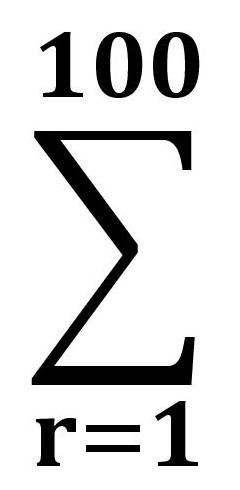 |
r=1+2+3+・・・+100 |
この場合、1+100=101,2+99=101,3+98=101,・・・,50+51=101、というように、50個の101が存在する。
すなわち、50×101=5,050が合計となる。これを数式で表現すれば、次式のように、関数で表示できる。
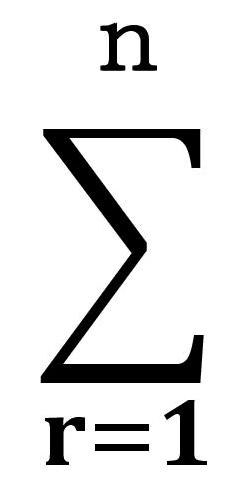 |
r=1+2+3+・・・+n |
|
| = |
| 1 |
 |
| 2 |
|
n(n+1) |
[n=100] |
また、代表的な多項式の有限級数として、次に示すような、等差級数、等比級数、等がある。
等差級数
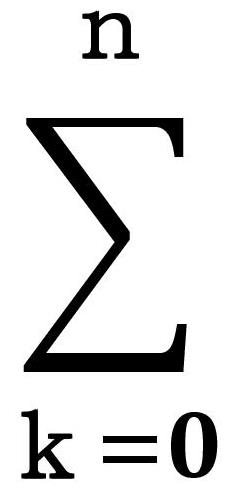 |
(a+kb)=a+(a+b)+(a+2b)+・・・+(a+nb) |
|
| = |
| n+1 |
 |
| 2 |
|
(2a+nb) |
等比級数
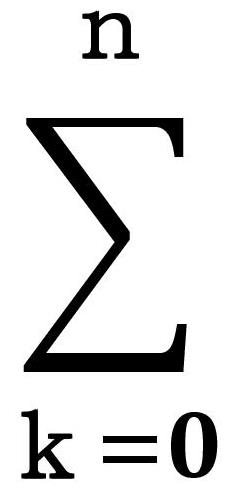 |
ark=a+ar+ar2+・・・+arn |
| = |
| a(1-rn+1) |
 |
| 1-r |
|
= |
| a(rn+1-1) |
 |
| r-1 |
|
[r≠1] |
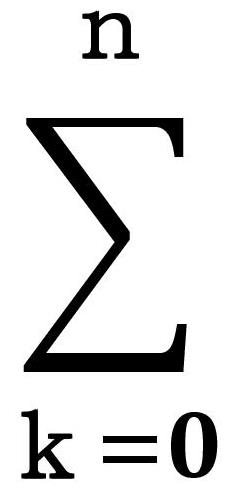 |
(a+kb)rk=a+(a+b)r+(a+2b)r2+ |
・・・+(a+nb)rn |
| = |
| a-(a+nb)rn+1 |
 |
| 1-r |
|
+ |
| br(1-rn) |
 |
| (1-r)2 |
|
[r≠1] |
注)r=1の時、等差級数になる。
3.自然数の級数展開・べき和
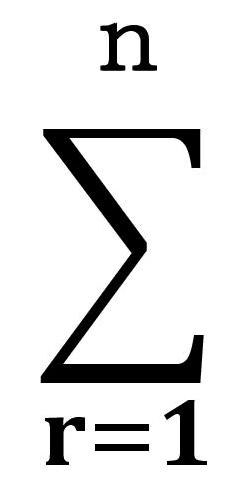 |
rk=1k+2k+3k+・・・+nk |
| k |
1k+2k+3k+・・・+nk |
| 1 |
| 1 |
 |
| 2 |
|
n(n+1) |
|
| 2 |
| 1 |
 |
| 6 |
|
n(n+1)(2n+1) |
|
| 3 |
| 1 |
 |
| 4 |
|
n2(n+1)2 |
|
| 4 |
| 1 |
 |
| 30 |
|
n(n+1)(2n+1)(3n2+3n-1) |
|
| 5 |
| 1 |
 |
| 12 |
|
n2(n+1)2(2n2+2n-1) |
|
| 6 |
| 1 |
 |
| 42 |
|
n(n+1)(2n+1)(3n4+6n3-3n+1) |
|
| 7 |
| 1 |
 |
| 24 |
|
n2(n+1)2(3n4+6n3-n2-4n+2) |
|
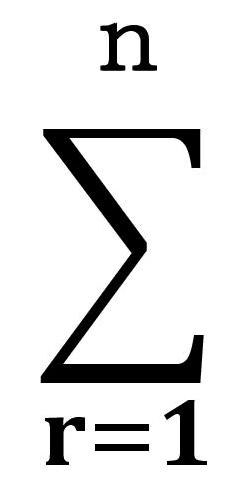 |
(-1)r-1rk=1k-2k+3k-+・・・+(-1)n-1nk |
| k |
1k-2k+3k-+・・・+(-1)n-1nk |
| 1 |
(1/2)(n+1) [n:奇数]
-(1/2)n [n:偶数] |
|
| 2 |
| (-1)n-1 |
| 1 |
 |
| 2 |
|
n(n+1) |
|
| 3 |
(1/4)(2n-1)(n+1)2 [n:奇数]
-(1/4)n2(2n+3) [n:偶数] |
|
| 4 |
| (-1)n-1 |
| 1 |
 |
| 2 |
|
n(n+1)(2n+1)(n2+n-1) |
|
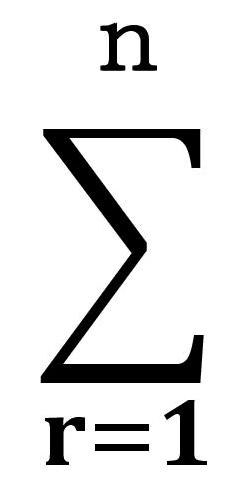 |
(2r-1)k=1k+3k+5k+・・・+(2n-1)k |
| k |
1k+3k+5k+・・・+(2n-1)k |
| 1 |
n2 |
| 2 |
| 1 |
 |
| 3 |
|
n(4n2-1) |
|
| 3 |
|
4.べき級数
べき級数は次のような形をとる。
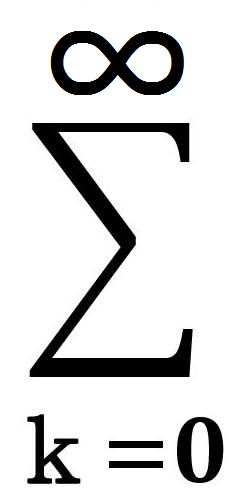 |
akxk=a0+a1x+a2x2+・・・+akxk+・・・ |
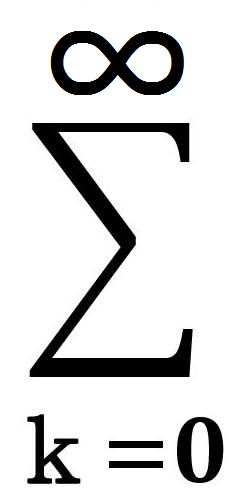 |
ak(x-c)k=a0+a1(x-c)+a2(x-c)2+・・+ak(x-c)k+・・ |
ここで、a0,a1,a2,・・・,ak,・・・は定数(複素数)、cは1つの複素数、xは変数である。
この場合、x-cのべき級数に対して、この級数は点cを中心としたべき級数と呼ばれる。また、このべき級数に対して、次の事実が成立する。
- このべき級数に対して、定数R(0≦R≦∞)が定まり、∣x-c∣<Rを満足するすべてのxに対して、べき級数は絶対収束する。
また、∣x-c∣>Rを満足する任意のxに対して、べき級数は発散する。なお、このような定数Rはべき級数の収束半径と呼ばれ、円∣x-c∣<Rをべき級数の収束円という。
特に、R=0の時はべき級数は点x=cだけで収束し、R=∞の時はべき級数はすべてのxに対して絶対収束する。
- 収束半径RがR>0を満たす時、べき級数はその収束円の内部で、項別に微分、積分ができる。すなわち、収束円の内部でべき級数の和f(x)から、微分すれば次のf(x)'が得られる。
| f(x) |
=a0+a1(x-c)+a2(x-c)2+・・+ak(x-c)k+・・ |
f(x)'=[a0]'+[a1(x-c)]'+[a2(x-c)2]'+・・+[ak(x-c)k]'+・・
=a1+2a2(x-c)+・・+kak(x-c)k-1+・・ |
また、収束円の内部にある任意の曲線Cについて、積分すれば、次式が成立する。
 |
f(x)dx |
=a0dx+a1(x-c)dx+a2(x-c)2dx+・・+ak(x-c)kdx+・・ |
- 収束半径Rとすれば、次の極限が存在する。
| 1/R= |
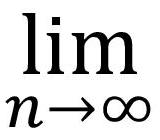 |
∣bn+1/bn∣ |
| 1/R= |
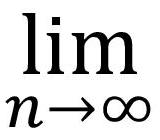 |
n√(∣bn∣) |
(簡単な事例)
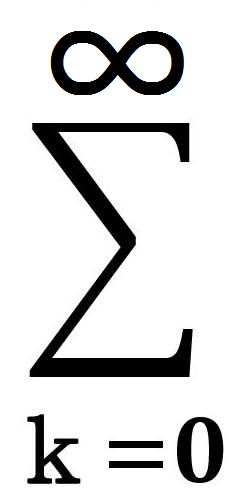 |
xk=1+x+x2+・・・+xk+・・・ |
このべき級数の場合、収束半径R=1である。また、収束円∣x∣<1内で、この級数の和は1/(1-x)となる。
5.テイラー展開
与えられた関数について、級数展開ができるかどうかを考える。いま、関数f(x)は領域D内で正則関数であるとする。正則関数とは、複素関数(複素数を変数とし、複素数に値をもつ関数)の内、定義域(対象領域)の全ての点で、微分可能な関数のことである。
そして、領域D内の任意な1点x=aを中心として、この領域D内にある最大の円の半径Rとする時、関数f(x)は、この円の内部∣x-a∣<Rにおいて、次のようなべき級数に展開できる。
| f(x)=f(a)+ |
|
|
|
(x-a)+ |
|
|
(x-a)2+・・・+ |
|
|
(x-a)n+・・・ |
|
このべき級数は、関数f(x)のaを中心とするテーラー展開と呼ばれている。特に、a=0としたものは、マクローリン展開と呼ばれている。
| f(x)=f(0)+ |
|
|
|
x+ |
|
|
x2+・・・+ |
|
|
xn+・・・ |
|
代表的な関数のマクローリン展開を次に示す。
| ex=1+x+ |
|
|
|
x2+ |
|
|
x3+・・・+ |
|
|
xn+・・・ |
|
| sinx=x- |
|
|
|
x3+ |
|
|
x5-+・・・+(-1)n |
|
|
x2n+1+・・・ |
|
| cosx=1- |
|
|
|
x2+ |
|
|
x4-+・・・+(-1)n |
|
|
x2n+・・・ |
|
5.フーリエ級数
フーリエ級数は三角関数を用いて周期関数を展開する。特に、任意の周期性を持つ時間関数は三角関数の無限級数の和として表すことができる。
F(t)=a0+a1cosωt+a2cos2ωt+・・・+ancosnωt
+b1sinωt+b2sin2ωt+・・・+bnsinnωt
| =a0+ |
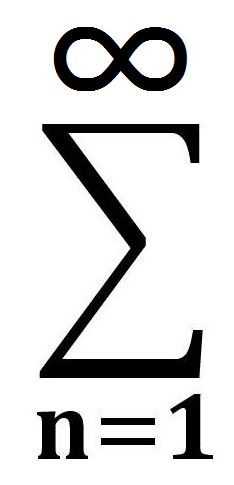 |
(ancosnωt+bnsinnωt) |
ここで、ωは角周波数(rad/sec)と呼ばれ、周波数f(1/sec:Hz)との間に、ω=2πfの関係がある。つまり、時間関数は周期関数(周波数関数)に変換できる。
この時、展開係数のa1,・・・,anおよびb1,・・・,bnは波の振幅の周波数成分に相当する。
なお、a0は周波数0成分、すなわち直流の周波数成分となる。
展開係数(振幅の周波数成分)の求め方
-
最初に、直流の周波数成分a0を求める。波の成分のcos波およびsin波は、1周期(0~2π)を捉えると、その面積が0になる。どんなに複雑な波でも、その波のそれぞれの周期T=2π/ω=1/f(周波数の逆数)について、
1周期(0~2π)分の面積で捉えれば、最終的に、直流の周波数成分a0と周期Tとの積だけが面積として残る。
つまり、この面積を周期Tで割れば、直流の周波数成分a0となる。結果的に、展開係数a0は、関数F(t)の周期Tにわたる平均を意味する。
| a0= |
|
 |
F(t)dt |
-
次に、anおよびbnを求める。波の成分のcos波およびsin波は、同じ周波数の波を掛け算した時以外はすべて面積が0になる。
したがって、a1を求める場合、F(t)にcosωtを掛け、得られた面積をT/2で割る。
他のanおよびbnも同様に求まる。
| an= |
|
 |
F(t)cosωtdt |
| bn= |
|
 |
F(t)sinωtdt |
矩形波のフーリエ級数展開
矩形波をフーリエ級数に展開する。フーリエ級数は周期2πの周期関数で表現できる。
そこで、時間関数F(t)を周期関数f(x)で表現し、矩形波も周期2πに設定する。
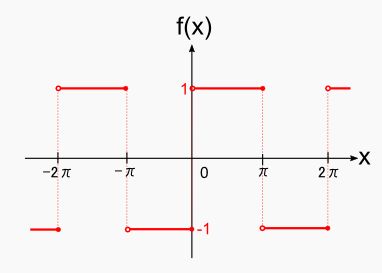 したがって、矩形波関数は次式(nは整数)で表示される。
したがって、矩形波関数は次式(nは整数)で表示される。
| f(x)= |
 |
1 0<x≦π |
| -1 π<x≦2π |
なお、全領域での矩形波関数は次式(nは整数)のようになる。
| f(x)= |
 |
1 2nπ<x≦(2n+1)π |
| -1 (2n-1)π<x≦2nπ |
次に、この矩形波関数をフーリエ級数で表した時の、フーリエ係数 a0,an,bn を求める。
そこで、フーリエ係数 a0は、周期関数f(x)を用いて、次のように置き換える。
| a0= |
|
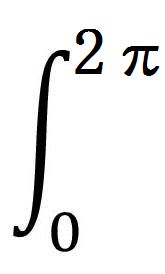 |
f(x)dx |
また、矩形波は、0<x≦π、π<x≦2π、で値が違う。そこで、積分する時、2つに分けて計算する。
| a0= |
|
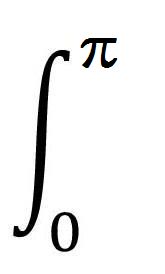 |
1dx+ |
|
|
|
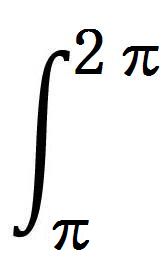 |
-1dx |
|
結果的に、a0はゼロになる。本来、a0は、その関数の1周期における平均のようなイメージであり、1と-1に振れる矩形波の場合、a0がゼロになるのは当然ともいえる。
次に、anを求める。anは、cos関数の係数であり、次式から計算する。
| an= |
|
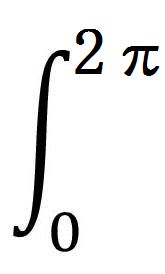 |
f(x)cos(nx)dx |
ここでも、積分する時、0<x≦π、π<x≦2π、2つに分けて計算する。
| an= |
|
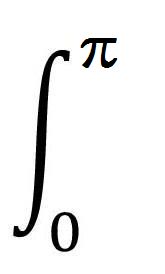 |
1・cos(nx)dx+ |
|
|
|
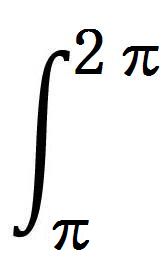 |
-1・cos(nx)dx |
|
最後は、bnを求める。bnは、sin関数の係数であり、次式から計算する。
| bn= |
|
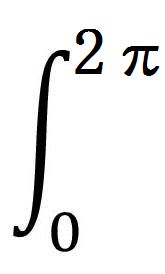 |
f(x)sin(nx)dx |
| bn= |
|
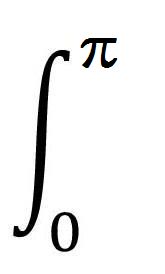 |
1・sin(nx)dx+ |
|
|
|
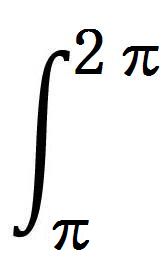 |
-1・sin(nx)dx |
|
この場合、cos(nπ)は,nが奇数ならば「-1」であり、nが偶数ならば「1」になる。
つまり、nが偶数か奇数かで,上式は、「4/nπ」になるか「0」になるかが決まる。
求めたいbnは、sin関数の係数であり、フーリエ係数は偶数でゼロ、奇数だけが残ればよい。つまり、
| f(x)=a0+ |
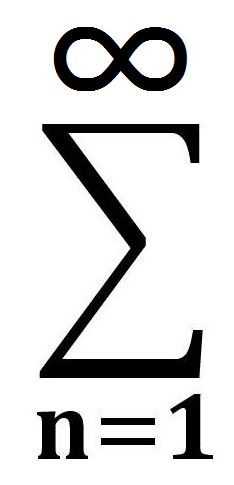 |
(ancosnx+bnsinnx) |
において、各フーリエ係数は、「a0=0」,「an=0」,「bn= 4/(2n-1)π」であり、sin関数の奇数のみを残すと、
次式が得られる。
| f(x)= |
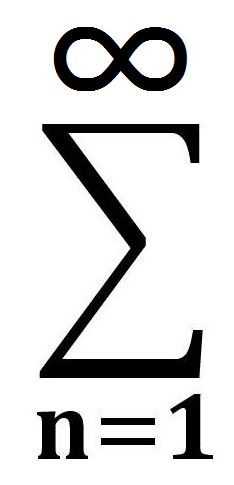 |
(4/π){1/(2n-1)}sin{(2n-1)x} |
| = |
(4/π){sin(x)+(1/3)sin(3x)+(1/5)sin(5x)+(1/7)sin(7x)+・・・} |
なお、全体にかかっている「4/π」は,単に矩形波の「高さ」を決めているだけを意味する。
6.ウエーブレット解析
ウエーブレットとは、三角関数や対数関数のような特定の決まった関数ではなく、局在する波を表す様々な関数の総称である。
ウエーブ(wave)は波、レット(lets)は小さなの複合語であり、時間と周波数の小さなさざ波のことをいう。
以上
(2013年3月24日)
戻る
|