-確率と統計-
確率とは、事象が実現すると期待される割合のことである。確率を現実的な経験の世界と関連付ければ、何回でも繰り返すことができる何らかの試行行為があるとする。 そして、その試行行為の結果、起こり得る事象の定まった集まりを考えると、起こる事象もあれば、起こらない事象もある。 この事象全体の集まりを確率事象と呼び、多くの試行行為をn回繰り返し、起こる事象の回数がm回とするならば、mとnとの比、すなわちm/n(0≦m/n≦1)を事象が起こる確率(算術確率)という。
統計とは、対象となる集まりのある特性あるいは標識について、その全体としての特徴を定量的に表現することである。 事象を調査して、数量で把握し、得られた数値データ(統計量)を用いて、その性質を調べ、集まりの全体の特徴を定量的に表現する。 なお、一般に、集団的な事象や現象を数字で表したものは統計的データと呼ばれている。
1.確率分布
硬貨投げには、表と裏、2つの根本事象がある。サイコロ振りには、1から6まで、6個の根本事象がある。 この時、それぞれの事象に数値を割当てる。硬貨投げの表には1、裏には0を割当てる。サイコロ振りの1から6までは、数値の1から6を割当てる。 この根本事象に割当てる変数は確率変数と呼ばれる。また、その数値は確率変数の実現値であり、出現確率である。
確率変数Xの実現値(出現確率)x1,x2,・・・,xnが飛び飛びの値の時、Xは離散的確率変数と呼ばれる。Xの実現値が連続の時、Xは連続的確率変数と呼ばれる。 確率変数Xの可能な実現値の1つ、j番目の値xjをとる確率は、
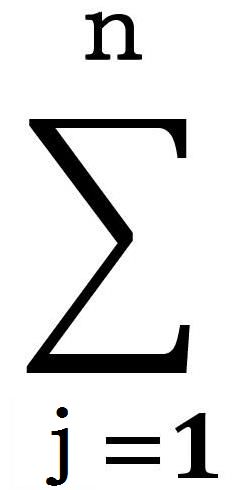 |
Wj=1 |
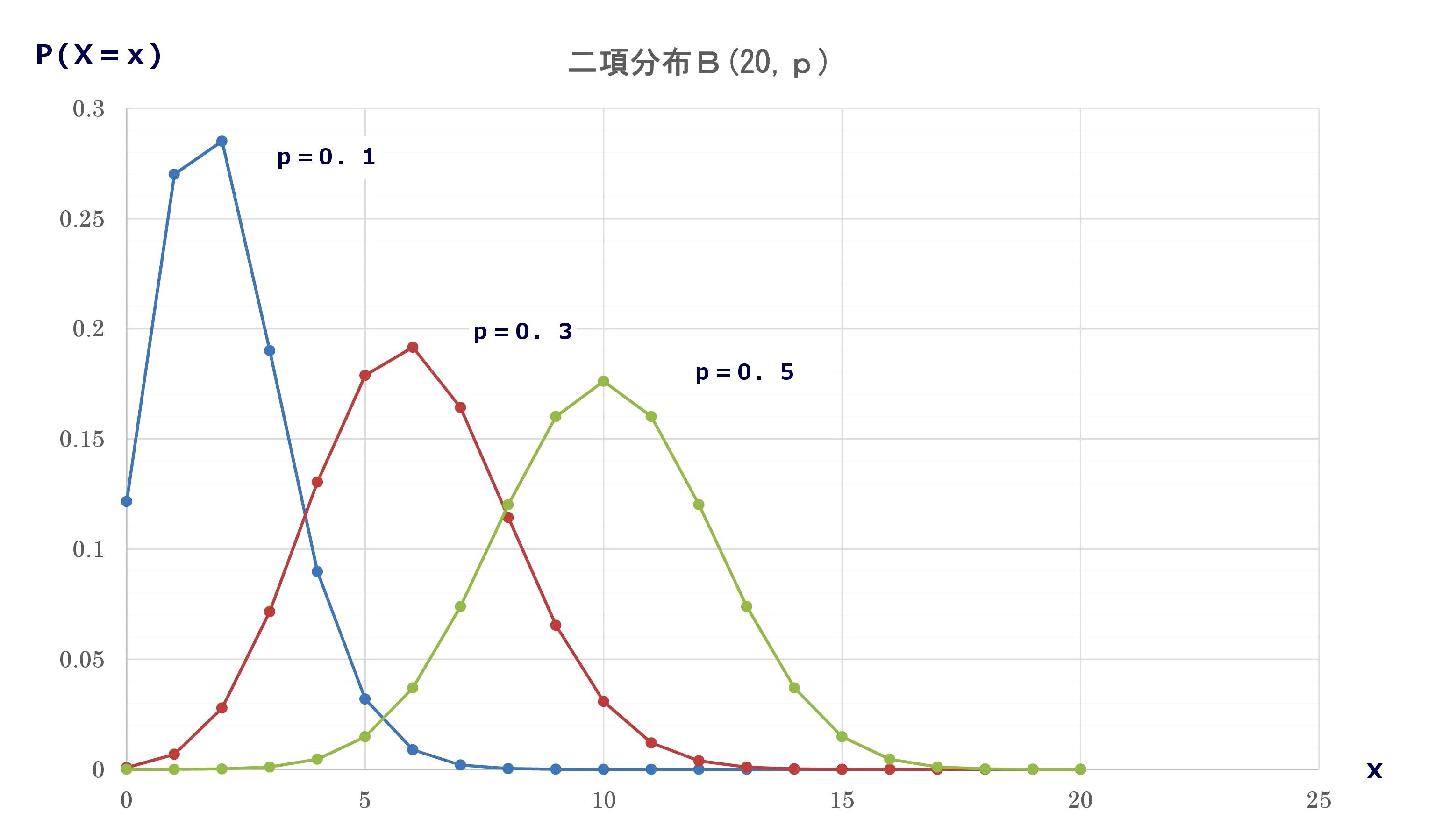
2.二項分布
二項分布は、試行行為の結果、成功か失敗のいずれかというような2つの事象に分けて考える場合を対象とする。 一般に、1回の試行で、ある事象Aが起こる確率をpとする。 n回の独立な試行を繰り返し、その事象Aが起こる回数Xの結果、ある値x(=0,1,2,・・・,n)になる確率は、
| nCx= |
|
3.正規分布
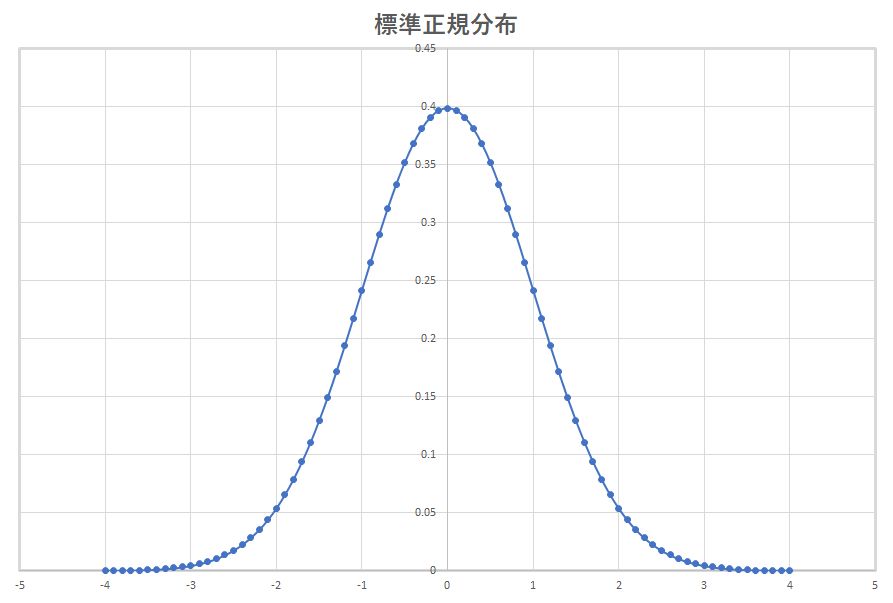
正規分布はガウス分布とも呼ばれ、平均値の付近にデータの分布が集積するような連続的な変数に関する確率分布である。正規分布の確率密度関数p(x)は、次式で表示される。
| p(x)= |
|
exp(-(x-μ)2/(2σ2)) |
| (-∞<x<∞) |
| p(x)= |
|
exp((-x)2/2) |
| (-∞<x<∞) |
大数の法則
一定の条件下で、繰り返し測定して得られる結果の平均値は、平均する値の個数を増やすことで、次第にある一定値に近づくようになる。つまり、母数のサンプル数nが大きければ、そのサンプル平均(標本平均)は、真の母平均に近づくようになる。
中心極限定理
母数のサンプル数nが大きければ、そのサンプル平均と真の母平均の差が従う分布は、平均値0、分散σ2/nの正規分布に近づく。すなわち、大数の法則も中心極限定理もサンプル平均の振る舞いに関する定理であり、サンプル数を大きくするとサンプル平均が次第に真の母平均に近づくというのが大数の法則、サンプル平均と真の母平均との差がどれくらいのスピードでどのように近づくのかを明確したのが中心極限定理と云える。
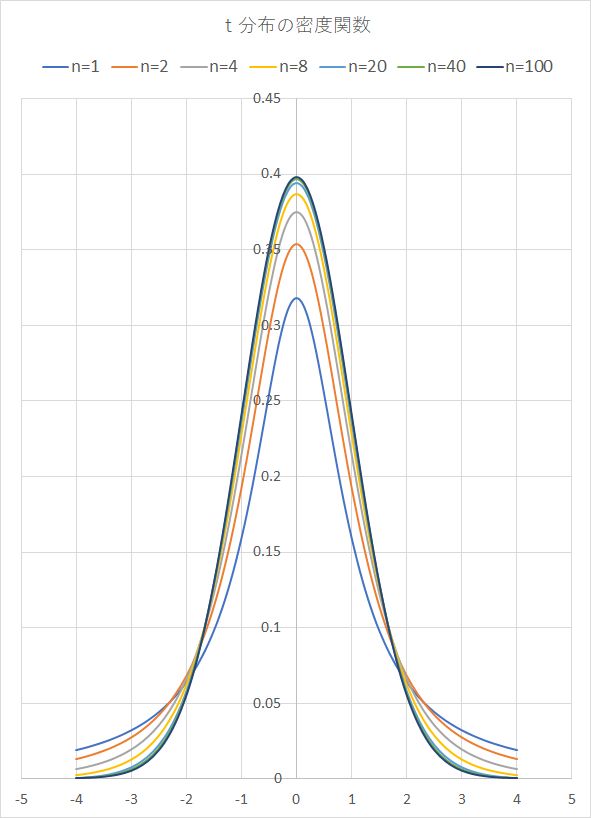
4.t分布
正規分布は、母平均μと母分散σ2のみで示される。しかし、一般には、母集団から標本をサンプリングし、母平均の代わりに標本平均で代用する。この場合、この標本平均がどれほど母平均に近いかが問題となる。標本平均が正規分布を示すには、標本数が非常に多くすることが前提となる。標本数が少ない場合、一般には。正規分布を示さない。 この場合、標本平均をどのように評価すればよいのか? 母標準偏差σの代わりに、標本標準偏差 ux (=√{1/(n-1)・Σ(xi-x~)2} )を用いて、t = (x~-μ)√n/ux = (x~-μ)√(n-1)/sxとおくと、t は平均0の t = 0 に関して対称な分布になる。
結果的に、t分布の確率密度関数は、次のように表示される。
| p(x)= |
|
(1+t2/n)-(n+1)/2 |
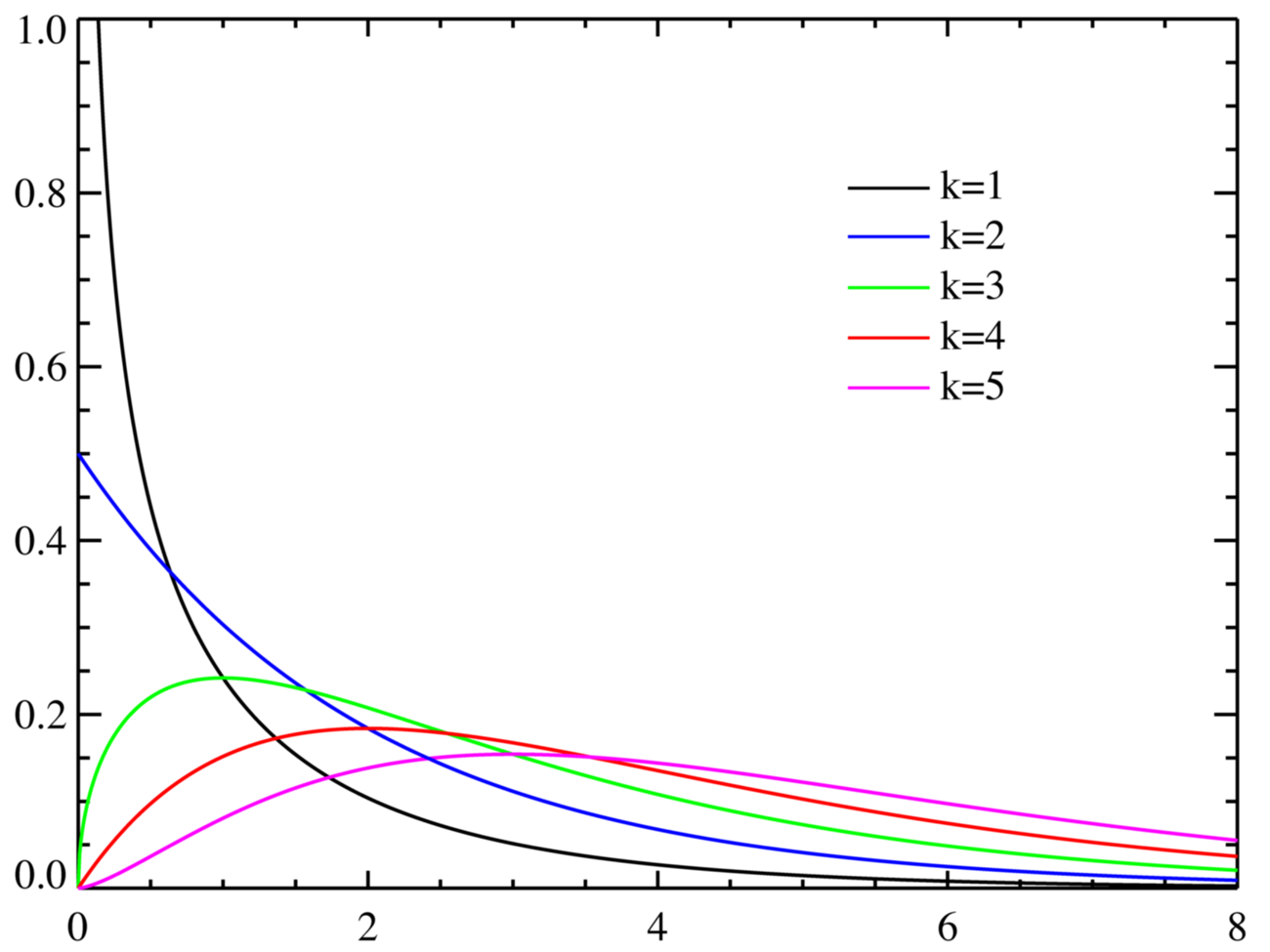
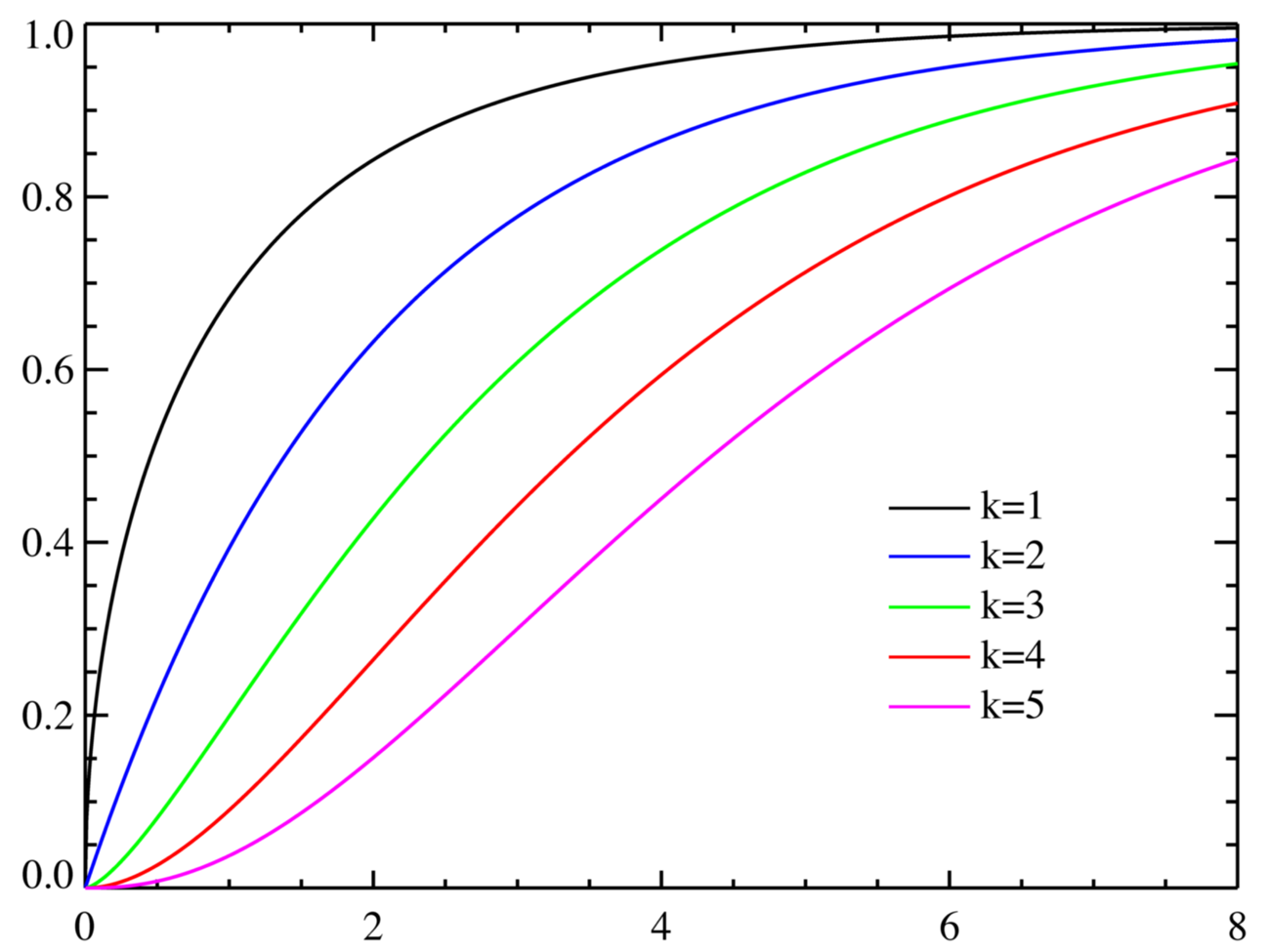
5.カイ2乗分布
カイ二乗分布(χ2分布)は、確率分布の一種、推計統計学で最も広く利用される。ヘルメルトにより発見され、ピアソンにより命名された。 独立に標準正規分布に従う k 個の確率変数 X1, …, Xk をとる。このとき、統計量の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。 この分布は、自由度 k に応じて、下図のような形をとる。 図を見れば分かるように、どの自由度 k でも、ある一定以上 Z が大きいならば、Z が大きいほどその確率が低くなることが分かる。 このことは、大まかに言えば、「正規分布でランダムで値をとったのであるから、その値を用いて高々二乗和をとった程度の数値 Z がとてつもなく大きくなる確率は少ないはずである」と解釈できる。 統計的仮説検定にカイ二乗分布が用いられるのはこの性質のためである。 例えば、「データが意味のないノイズ要素である可能性はたったの5%以下であるから、このデータには意味があるはずである」という解釈が行われる。 普通はこれを
6.ポアソン分布
統計学および確率論において、ポアソン分布(Poisson distribution)は、所与の時間間隔で発生する離散的な事象を数える特定の確率変数 X を持つ離散確率分布のことである。 ある離散的な事象に対して、ポアソン分布は所与の時間内での生起回数の確率を示し、指数分布は生起期間の確率を示す。 数学者シメオン・ドニ・ポアソンが確率論に基づき1838年に発表した。
定数 λ > 0 に対し、0 以上の整数を値にとる確率変数 X が
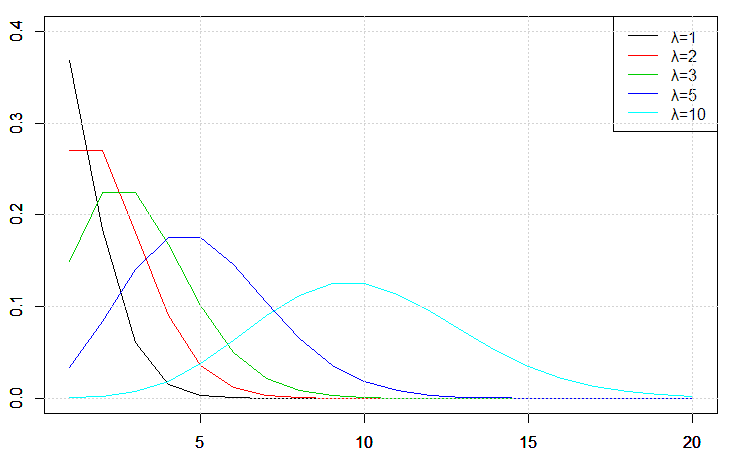
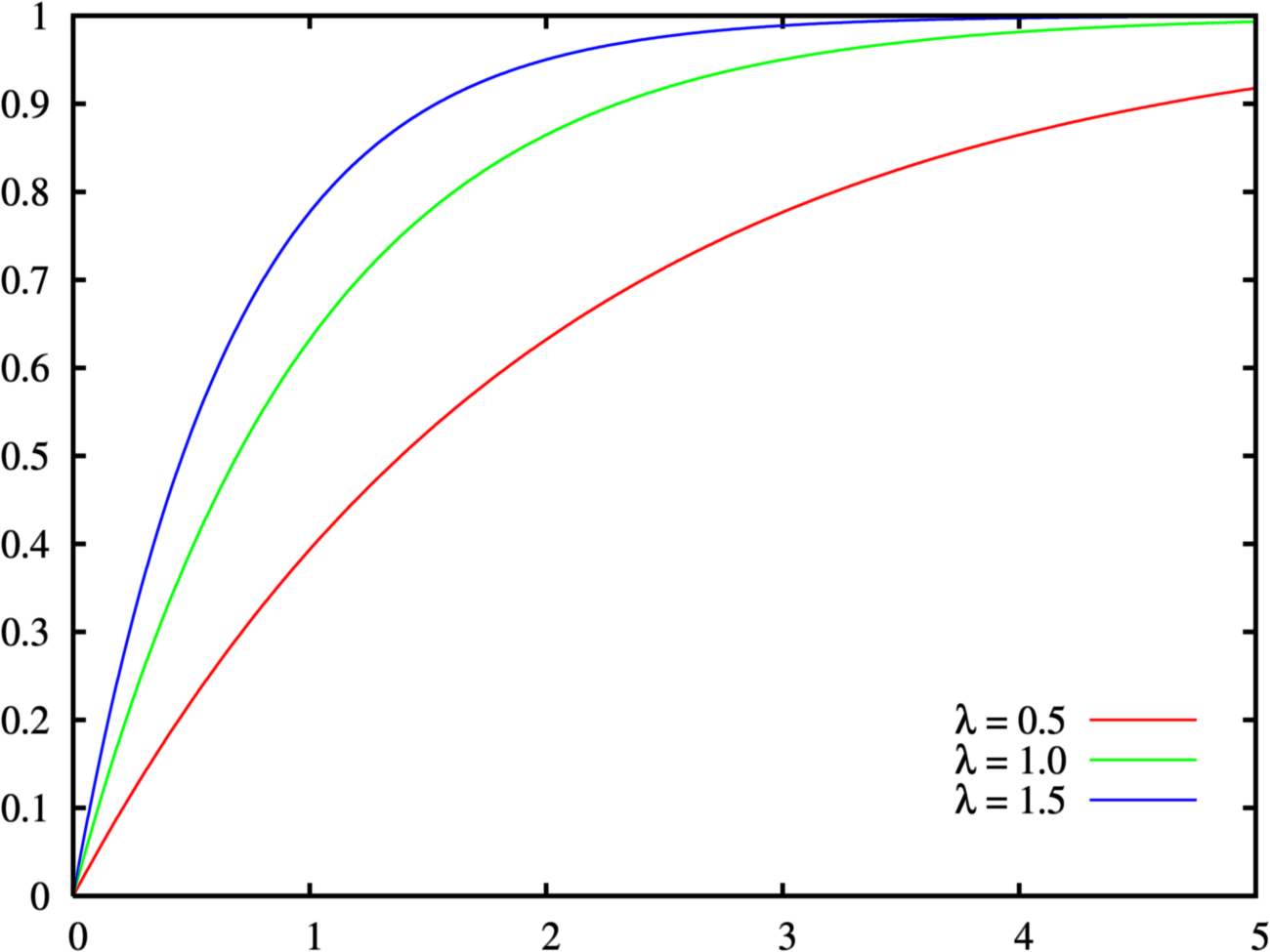
ポアソン分布のグラフを下図に示す。横軸はある期間に平均して回起こる現象が実際に起こる回数k、縦軸はそのときの確率を表す。 ポアソン分布は、λが大きくなると、グラフは右側へスライドし、右に裾を引いているグラフがだんだん左右対称に近づき、次第に正規分布に近づく。
7.指数分布
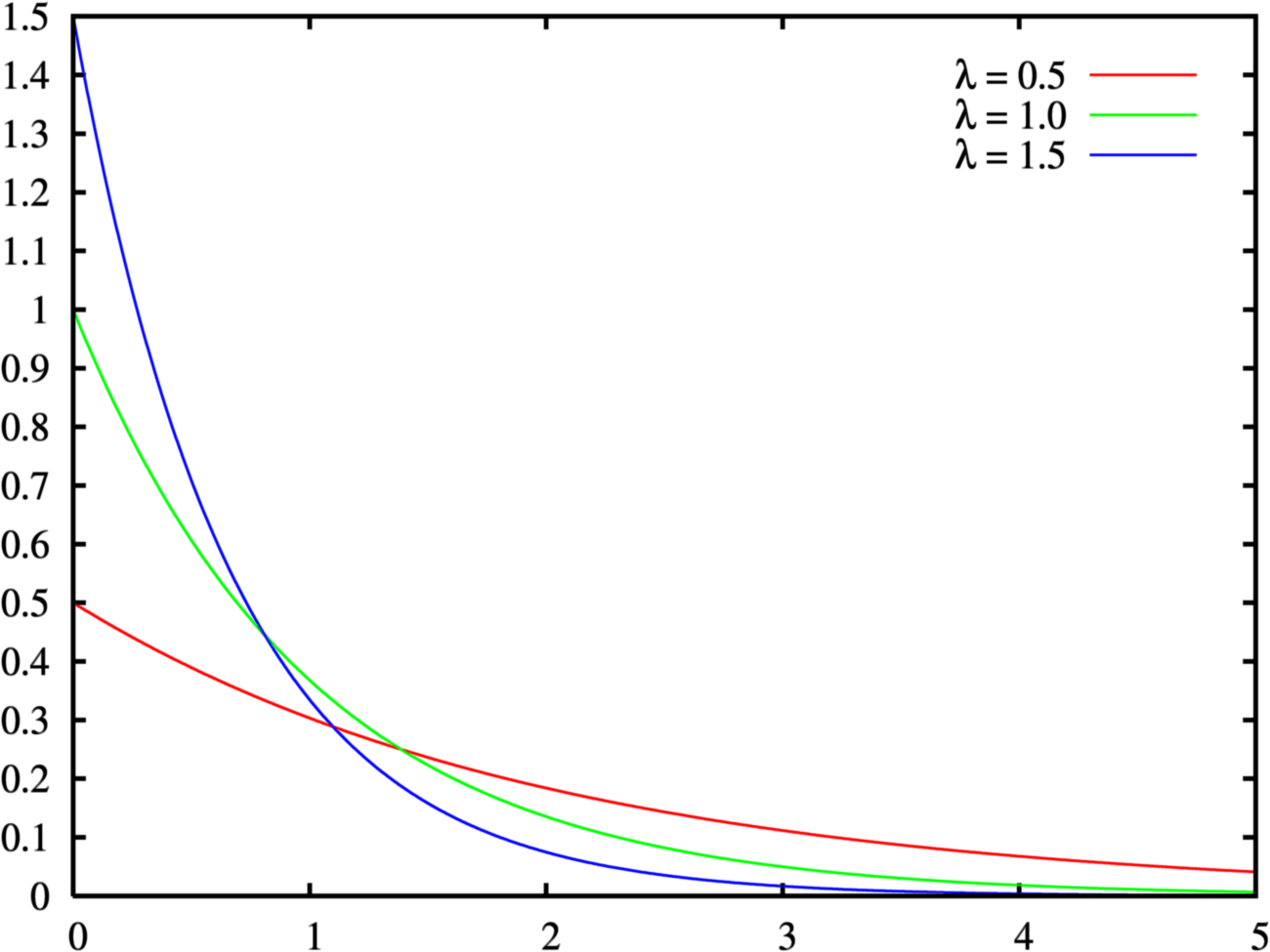
指数分布(exponential distribution)は、確率論および統計学における連続確率分布の一種である。 これは例えばポアソン過程——事象が連続して独立に一定の発生率で起こる過程——に従う事象の時間間隔を記述する。
指数分布は、母数 λ > 0 に対して確率密度関数が、
となる[2]。
尺度母数 θ = 1λ を用いると、確率密度関数の等価な定義は
8.F分布
F分布(Fdistribution)は、自由度がk1、k2のカイ二乗分布χ1~χ2(k1)、 χ2~χ2(k2)が互いに独立である場合、次式から算出されるFが従う確率分布のことである。 このときFは自由度(k1、k2)のF分布に従う。 F分布はt分布やカイ二乗分布と同様、自由度によって形が異なるが、t分布やカイ二乗分布と異なり、2つの自由度から分布の形が決まる。
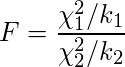
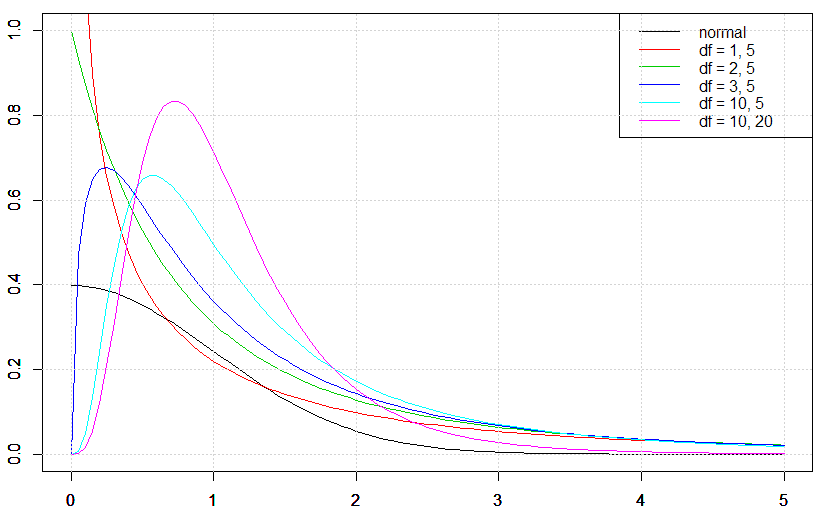
次のグラフは、自由度を変化させた時のF分布の形である。自由度(df=k1、k2)が(1, 5)、(2, 5)、(3, 5)、(10, 5)、(10, 20)の場合、 F分布(黒、赤、緑、青、水色、ピンク線)で表示される。
9.最小二乗法
得られたデータ(標本)に対して、近似的な直線方程式、
| J= | 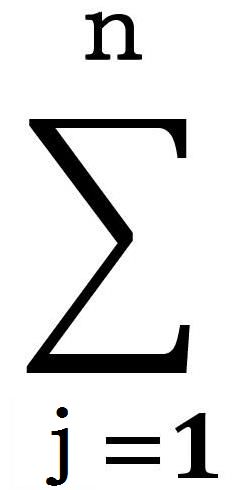 |
uj2= | 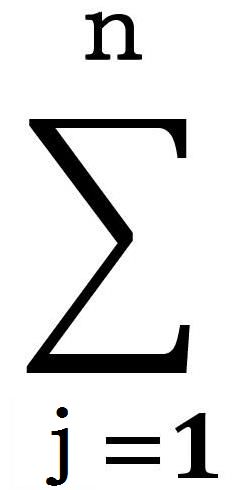 |
(Yj-aXj-b)2 |
一般に、関数Jを最小化にするには、数学的な微分の概念を用いる。 この場合、関数Jは、aとbを変数とするので、それぞれについて、微分して、それらを0と置き、最小化して、未知数のaとbを求める。
最初に、関数Jを変数aについて、微分(偏微分)する。
|
|
||||||||||
|
|
|
||||||||||
|
これら2つの式から、次式が得られる。
|
|
=0 |
|
|
=0 |
|
|
| n | X | Y | X2 | XY |
| 1 | 20 | 9 | 400 | 180 |
| 2 | 30 | 11 | 900 | 330 |
| 3 | 40 | 15 | 1,600 | 600 |
| 4 | 50 | 20 | 2,500 | 1,000 |
| 5 | 60 | 23 | 3,600 | 1,380 |
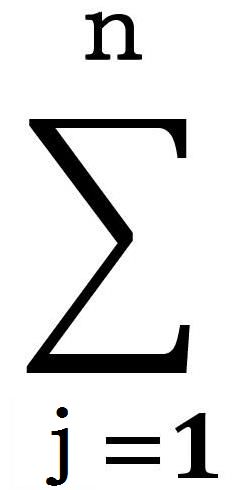 | 200 | 78 | 9,000 | 3,490 |
これらを連立方程式に代入すれば、次式を得る。
したがって、求めるべき最小二乗法の回帰直線として、次式を得る。
以上
(2013年3月24日)






