-特殊関数(付録)-
1.ガンマ関数(階乗関数)
ガンマ関数は、L. Euler によって、1729年に発見された。その動機は、自然数nに対して定義される階乗n!を、自然数ではないnの場合にも拡張しようとした。 この時、ガンマ関数を次の無限乗積で定義した。
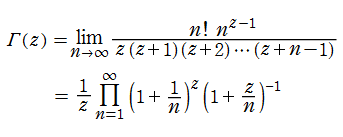
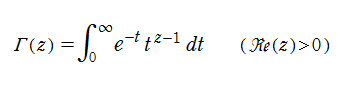
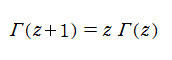
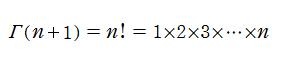
この他にも、「相補公式」 (または 「相反公式」 等) と呼ばれる関数等式や、「倍数公式」 および 「多倍数公式」など、 ガンマ関数は様々な関係式を満たす。
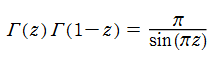
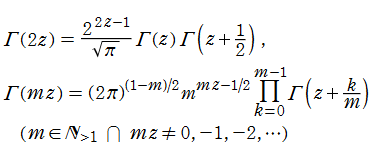
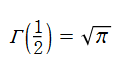
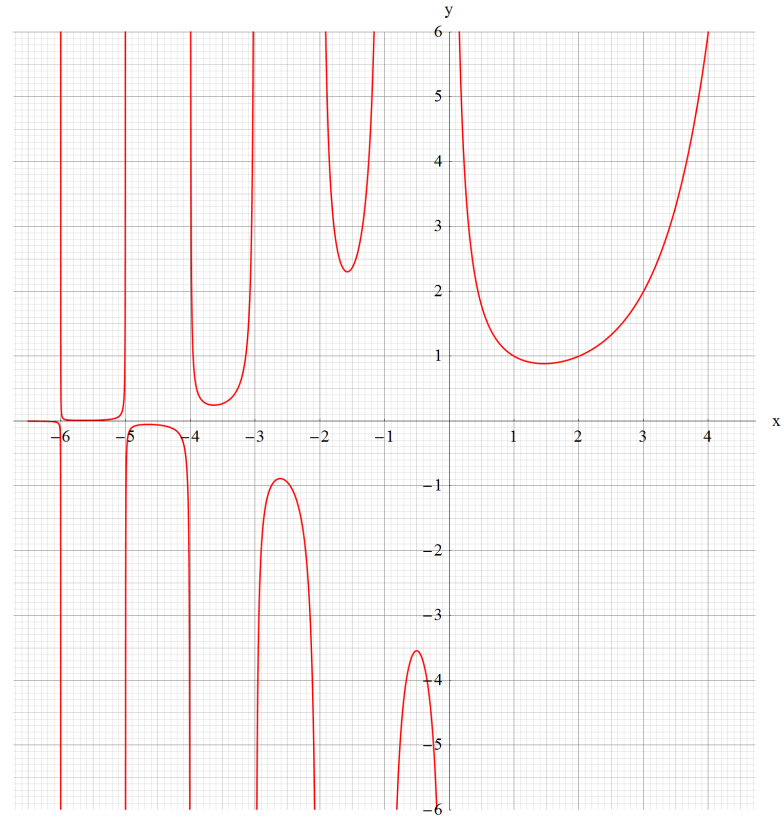
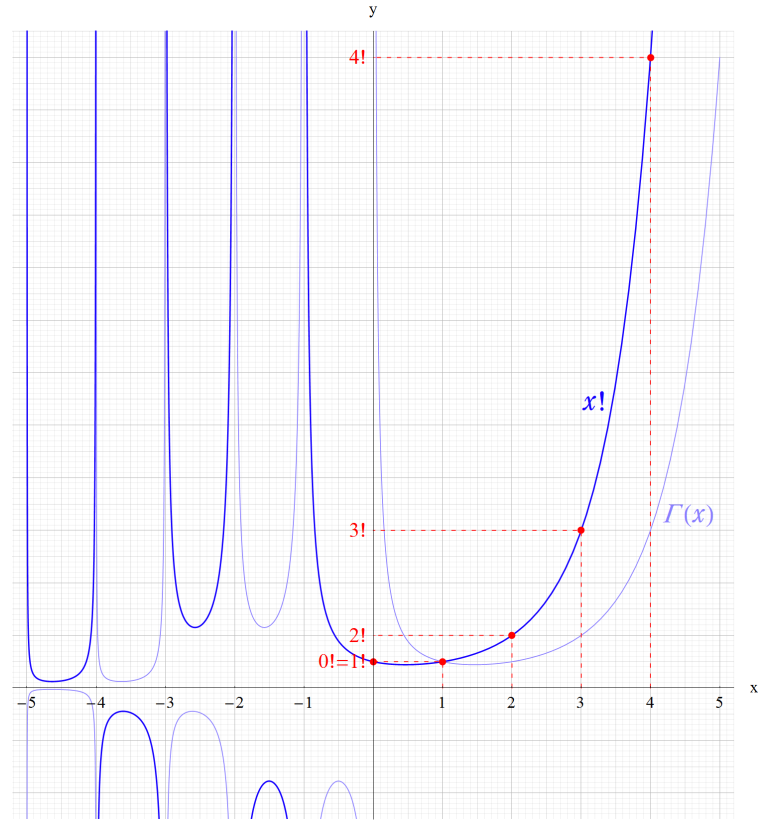
2.楕円関数
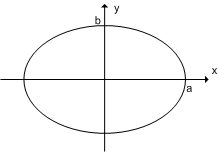
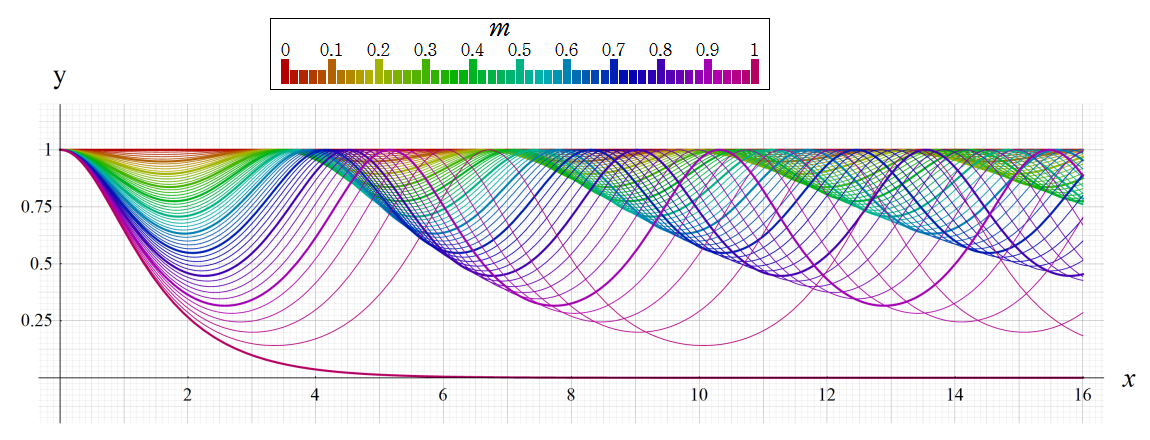
楕円は、原点Oを中心に、長軸a、短軸bとする。ここで、楕円の周の長さを求める。すると、楕円積分が必要になる。楕円関数は、楕円積分から定義される。 楕円積分は初等的に解けない。楕円関数を理解するには複素関数論が必要になる。楕円関数は周期関数、周期性のある現象を記述する。 しかも、三角関数よりも複雑、二重周期性という性質を持っている。また、楕円積分は、有限振幅の単振子の周期を求める問題にも応用される。 以下、楕円関数の初歩として、その手順を考えてみる。
楕円の周の長さは、楕円の周の座標を x=asinθ,y=bcosθ として求める。計算は第一象限の弧だけを求めて4倍する。
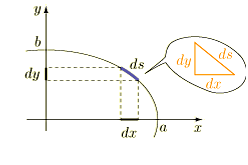
曲線の微小要素の長さ ds は,ピタゴラスの定理を使うと、次のように表せる。
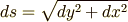
弧の長さはこれを全体に渡って積分すればよい。
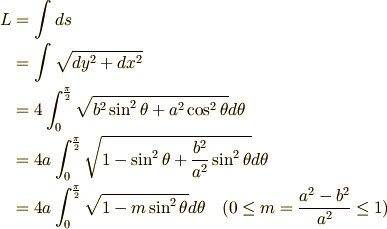
ここで、dx=acosθ・dθ,dy=-bsinθ・dθ,m=(a2-b2)/a2 である。
この積分は解析的に解けない。そこで、級数展開する。
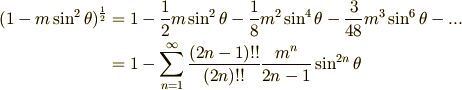
であり、この級数は m<1 の範囲で一様収束するので、和と積分順序を変更し、
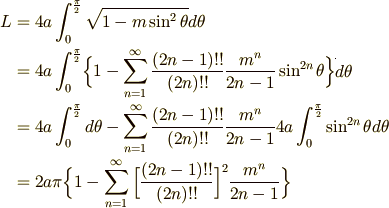
を得る。ここで、
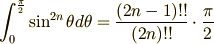
である。なお、円の場合は、a=b=r、m=0 であり、円周は、L=2πr になる。
楕円の周を求める過程で,簡単には解けない積分が出てきた。この積分は『第二標準形の完全楕円積分』と呼ばれる。 この積分を関数E(m)と名付け、第二標準形の完全楕円積分を級数展開で表示する。
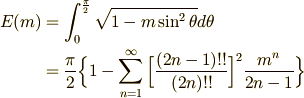
楕円積分には、この他に第一標準形と第三標準形がある。 第一標準形の完全楕円積分は次のように表わされ、通例 K(m) のように書かれる。
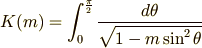
この積分も簡単には解けない。そこで,級数展開する。
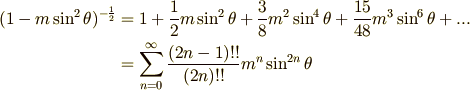
この級数もやはり m<1 の範囲で一様収束する。したがって、次のようにシグマの中を項別に積分することができる。
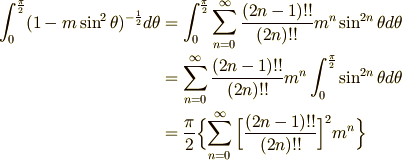
最後の sin の積分は,公式を使ったが、第一標準形の楕円積分も級数表示することがでた。 楕円関数は、ここで出てきた E(m) や K(m) から定義される。
|
楕円積分 次の積分は、第一種、第二種、第三種の楕円積分と呼ばれる。 母数kの代わりにパラメーターm=k2を用いることもある。 あるいはモジュラー角α=sin1kを用いることもある。 第一種完全楕円積分と第二種完全楕円積分 |
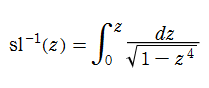
Gaussは、次の逆正弦関数の積分表示式から、逆関数の研究に興味を持ったようだ。
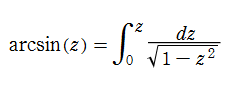
Gaussの楕円関数sl(z)とcl(z)には、三角関数の正弦と余弦に類似した次の関係がある。
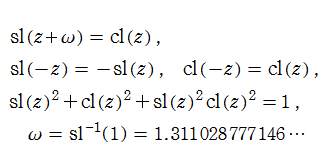
また、Gaussの楕円関数は、次の代数的加法公式をも満足する。
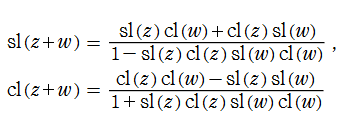
当初、Gaussは、これらを楕円関数ではなく、レムニスケート関数と称していた。レムニスケートとは連珠形のことである。 当時、楕円や双曲線およびレムニスケート(連珠形)など、種々の代数曲線の長さを求める問題(求長問題)の相互関係が研究されていた。
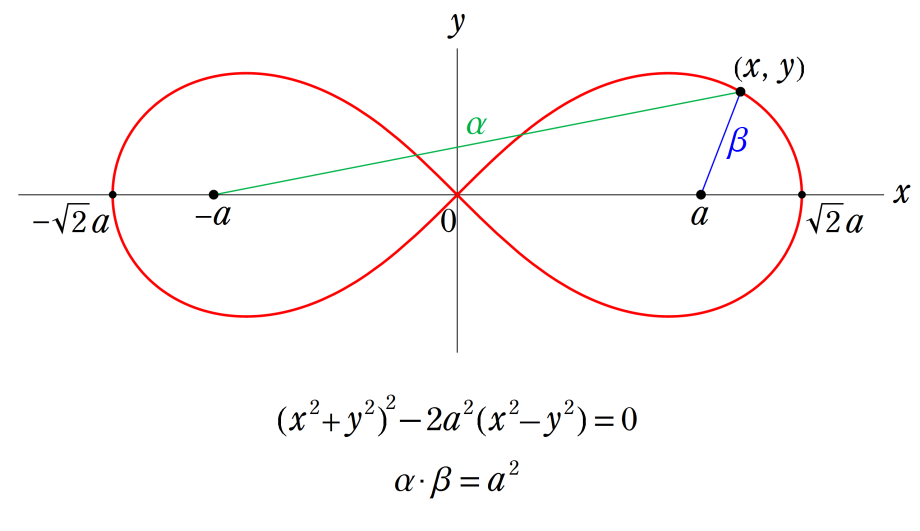
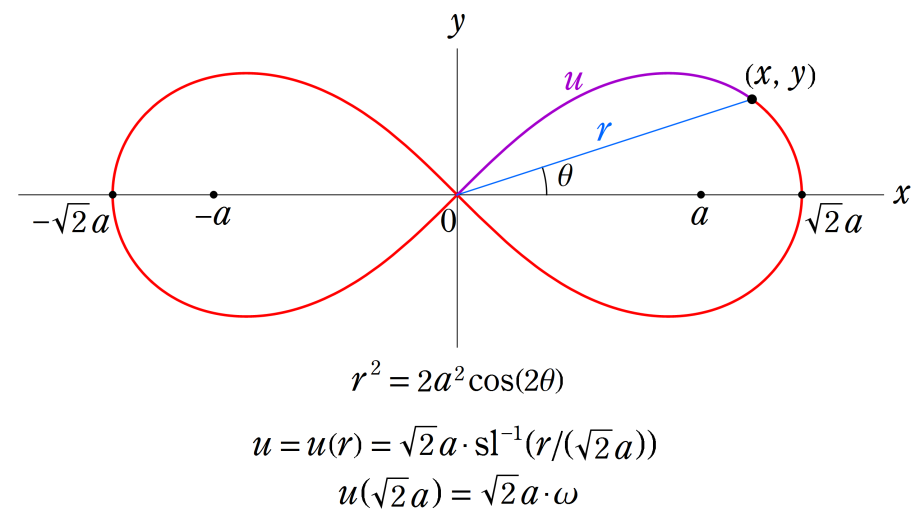
Gaussが楕円関数とその複素変数を考察し始めた理由の一つに、レムニスケートの等分問題がある。円の等分問題でも古代ギリシャ時代から大きく飛躍した。 その成果として、Gauss は、p=2^(2^n)+1が素数ならば、円周は定規とコンパスのみでp等分できることを証明した。 これをレムニスケート(連珠形)に拡張した。円の場合、三角関数の多倍角公式が根拠となるが、実数解しか生じない。 ところが、レムニスケートの場合、すなわち楕円関数のそれからは余分な複素数解も生じた。これが Gaussの考察を促すことになった。 ただし、すべての実数解が四則演算と平方根のみで明示可能なとき、定規とコンパスのみで等分できる。 レムニスケート(片側:第1・第4象限内)では、3等分, 4等分, 5等分, 17等分,… が可能となる。
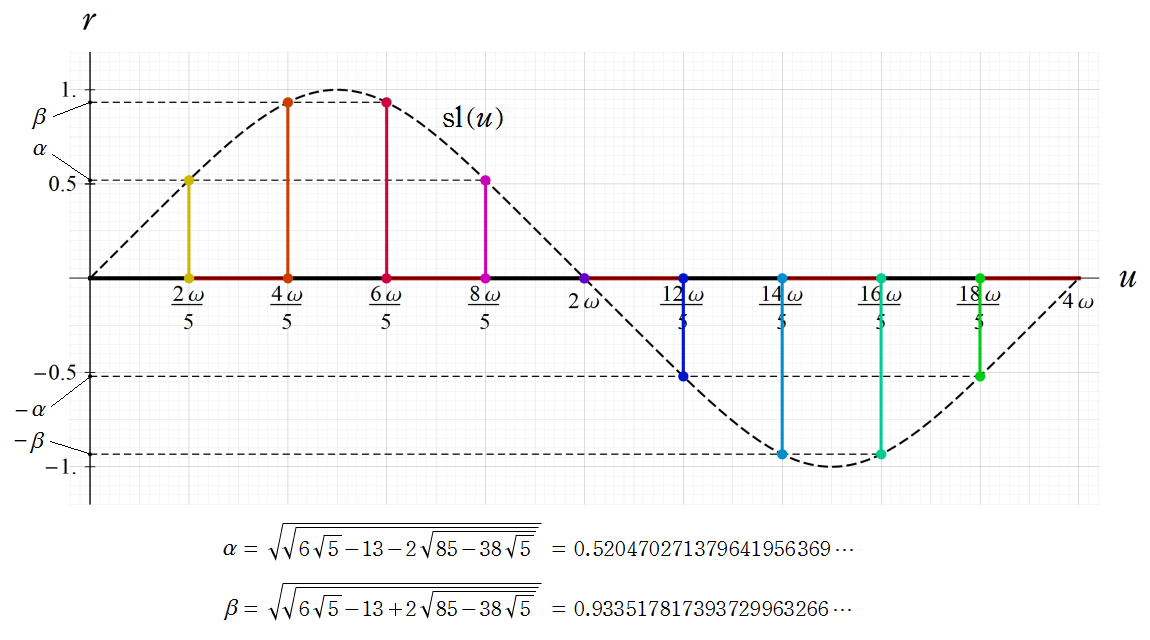
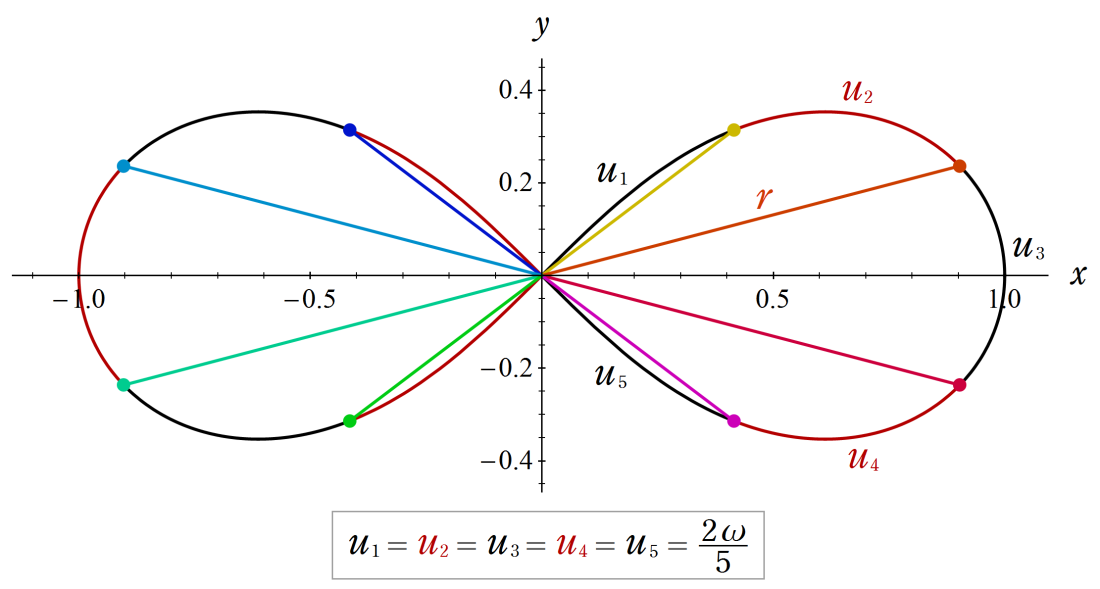
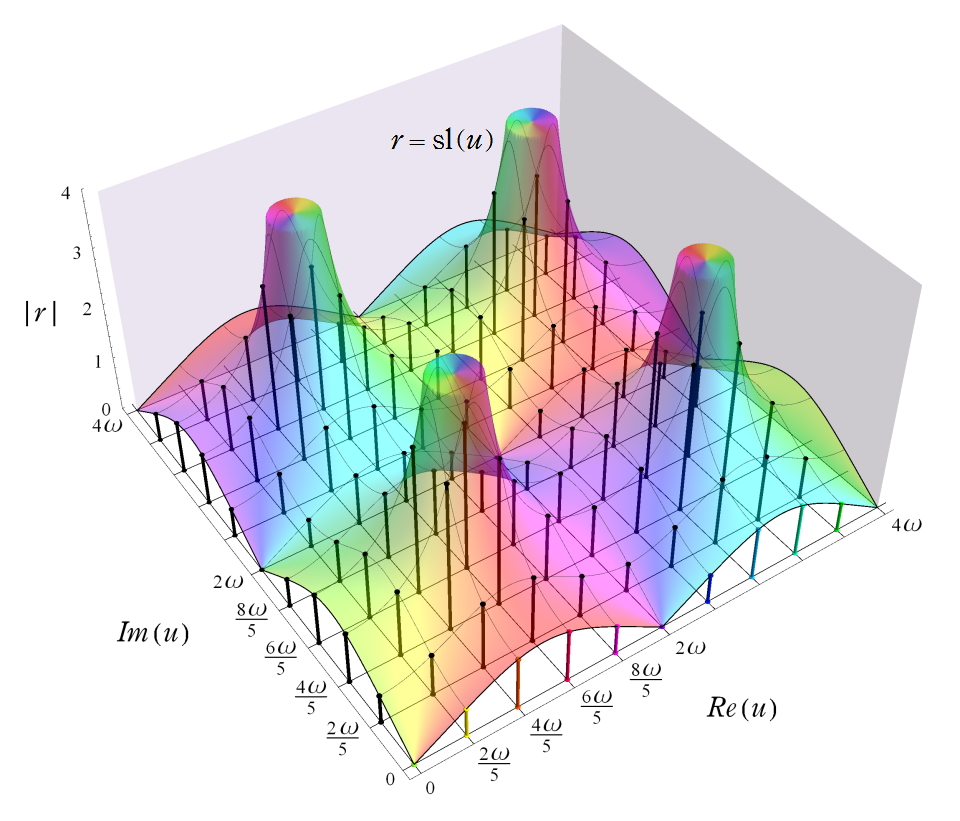
次の図は、レムニスケートの5等分から生じる25次方程式の実数解と複素数解が、格子等分点での Gauss の楕円関数値を示している。
Gaussの楕円関数は、虚数変数の場合、
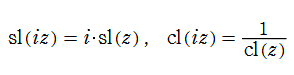
となり、楕円関数の二重周期性を満たす。
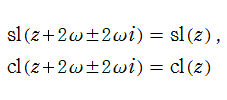
楕円関数の二重周期性とは、複素解析において、二方向に周期を持つ有理型二重周期関数のことをいう。 二重周期は、二つの線形独立な基本周期を持ち、その比が実数にならない (つまり、周期が作る平行四辺形が潰れていない) ことを言う。 また、その平行四辺形に含まれる極の位数の和は、2位を最小とする。これらの特徴にしたがって、楕円関数の具体的な表示式が直接与えられる。
厳密には、ガウス平面上で定義される有理型函数fであって、比 a/b が実数とはならない二つの複素数 a, b が存在して、 f(z) が定義される限り、全ての z に関して
が成立するものをいう。さらに、任意の整数 m, n に対して、
が成り立つことも従う。つまり、複素解析における楕円関数は、二方向に周期を持つ有理型二重周期函数のことをいう。 現在、楕円関数の定義は 「複素平面上の二重周期有理型関数」 と表現している。
なお、Gauss の楕円関数は、後述する Jacobi の楕円関数の特別な場合として、
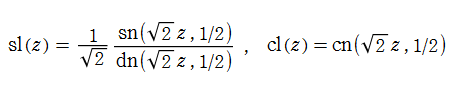
と表わせる。
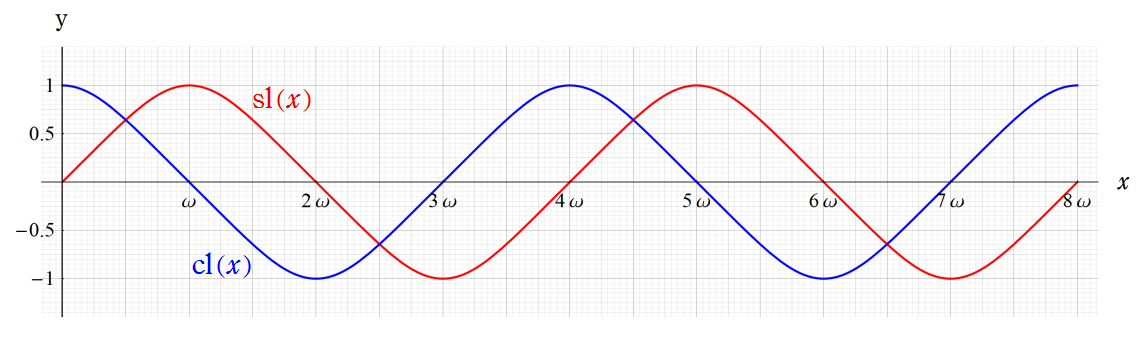
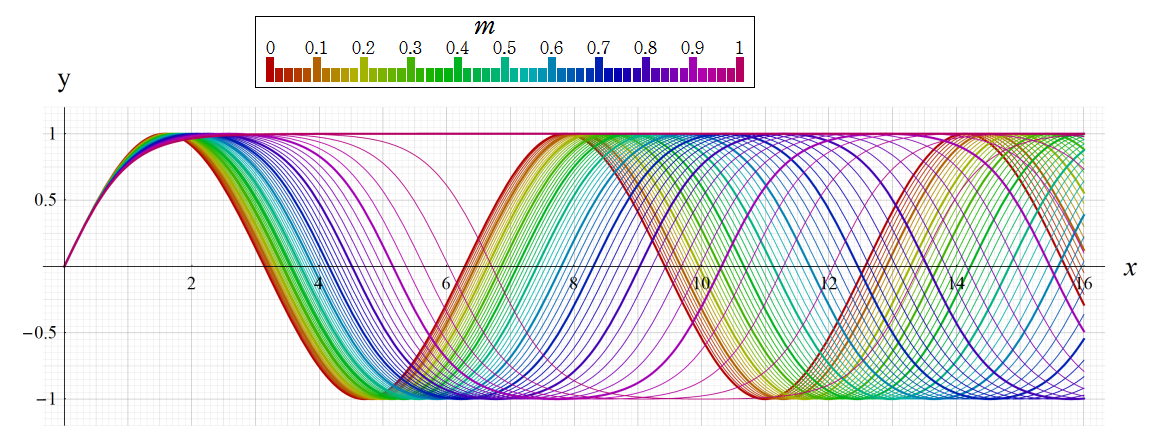
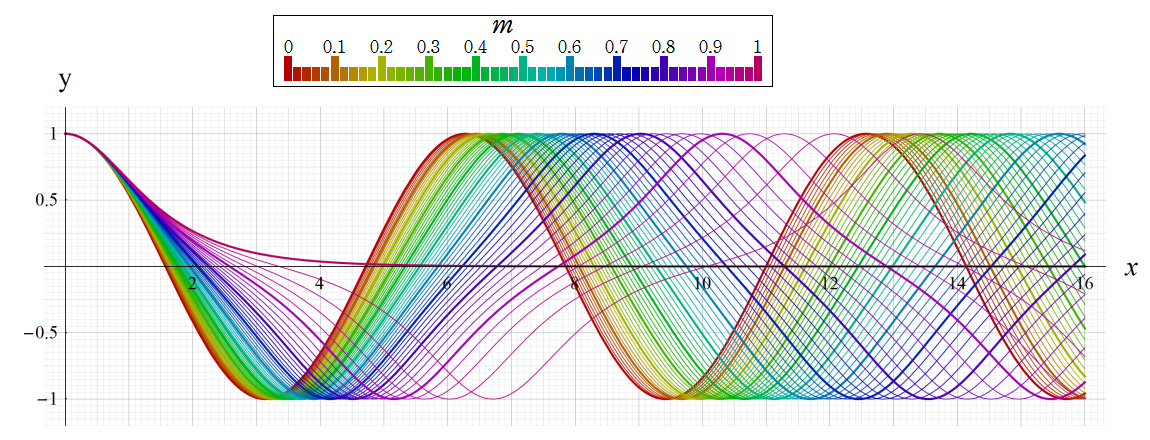
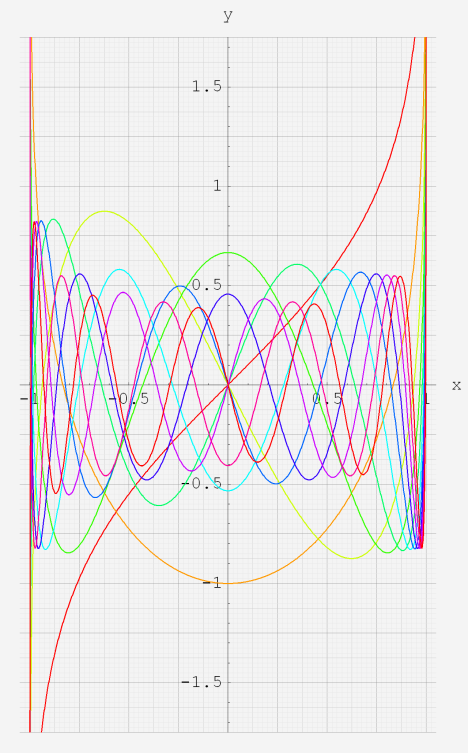
実変数の Gauss の楕円関数sl(x)およびcl(x)のグラフ。
三角関数に似ているが、波のスロープが三角関数よりも直線的である。
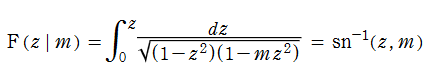
の逆関数であり、sn(z, m)と表記される。 併せてcn(z, m), dn(z, m)が Jacobi の楕円関数に追加される。これらは、三角関数に似た関係式、
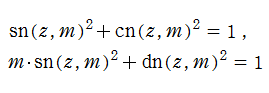
を満たすように定義される。また、mの値に係わらず、sn(z, m)は常に奇関数、cn(z, m), dn(z, m)は常に偶関数である。
Jacobi 楕円関数の導関数は、それ自身を用いて、
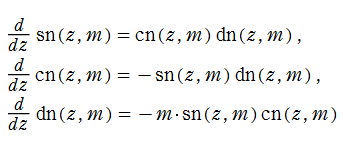
と表わされる。したがって、楕円関数を逐次微分して得られる任意位数の楕円関数、一般の基本周期を持つ楕円関数など、 すべての楕円関数はこの3種類の関数で表わすことができる。
また、Jacobi の楕円関数は、三角関数と同様に、次の代数的加法公式を満たす。
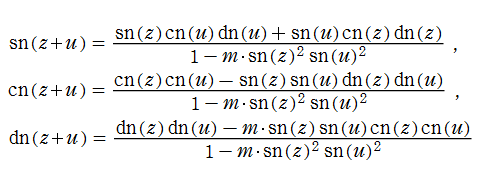
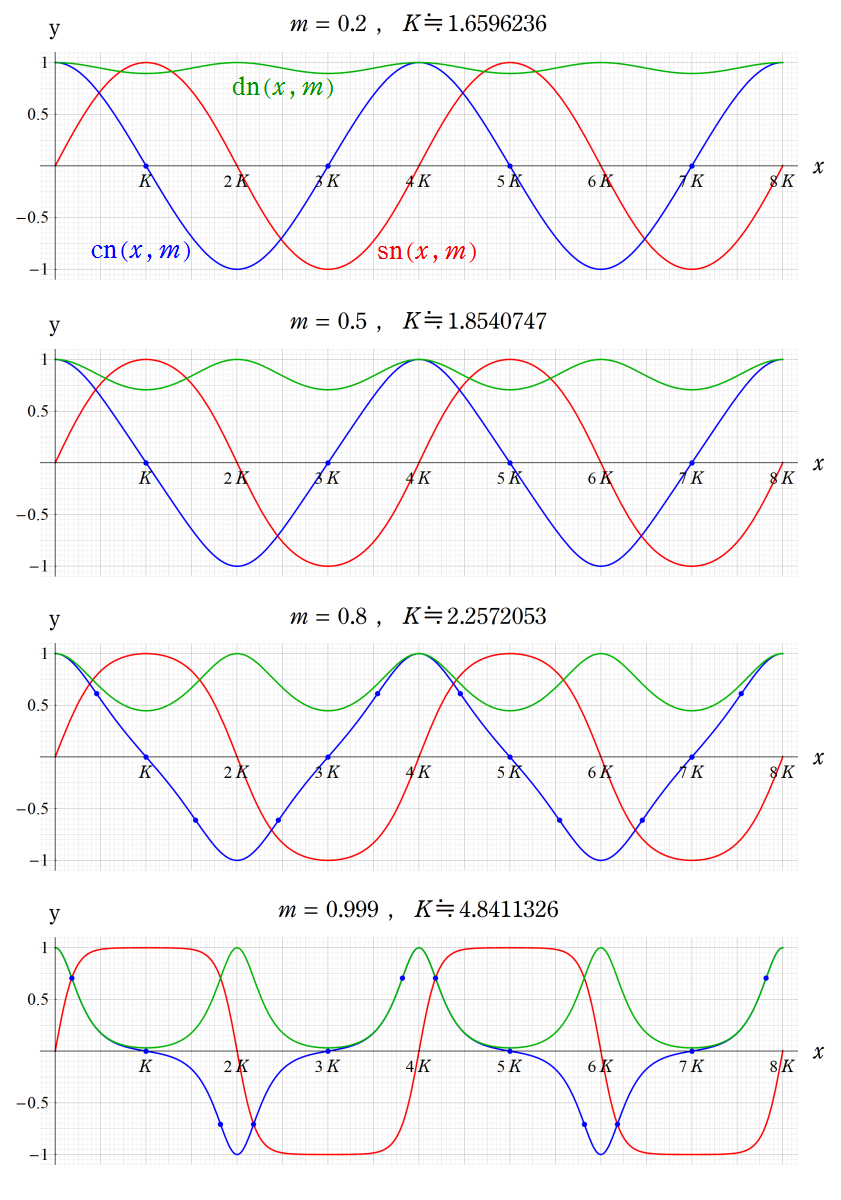
② m<0の場合。曲線上の点はsn(x, m)の変曲点であり、m<-1でその個数が増える。
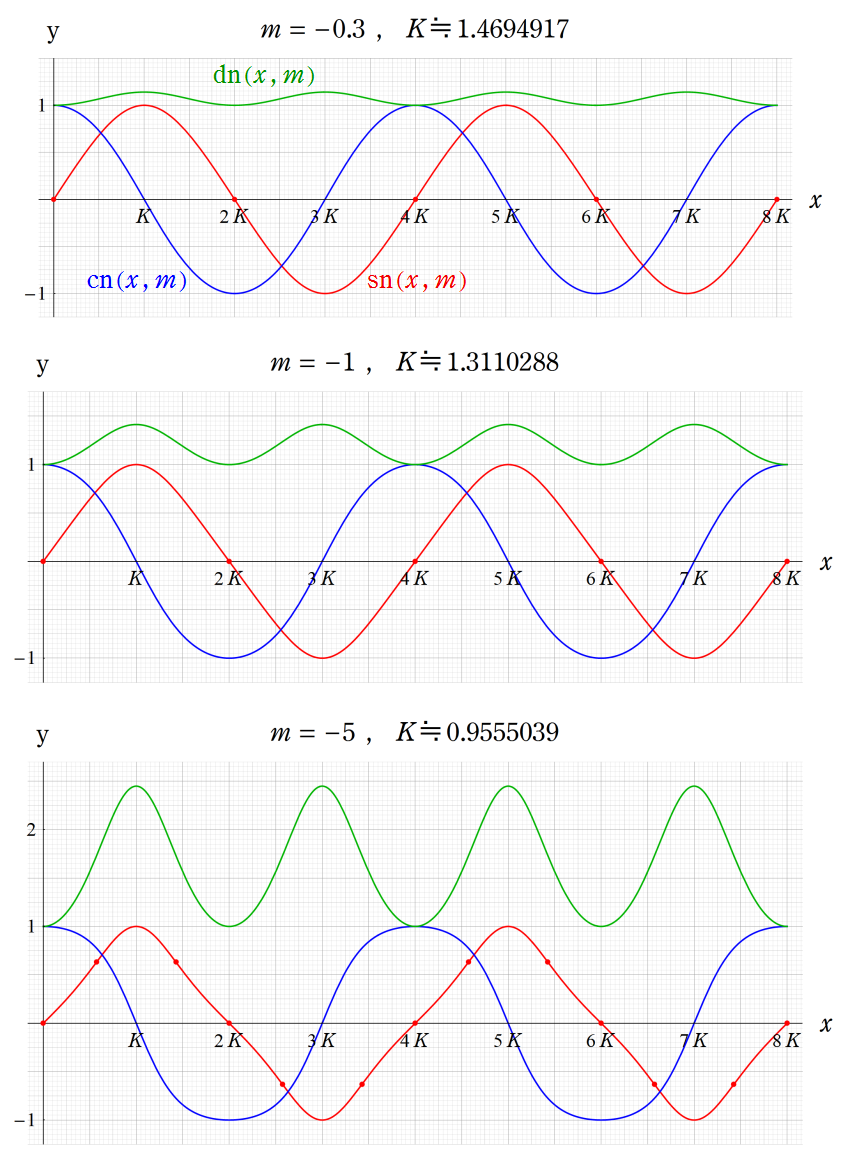
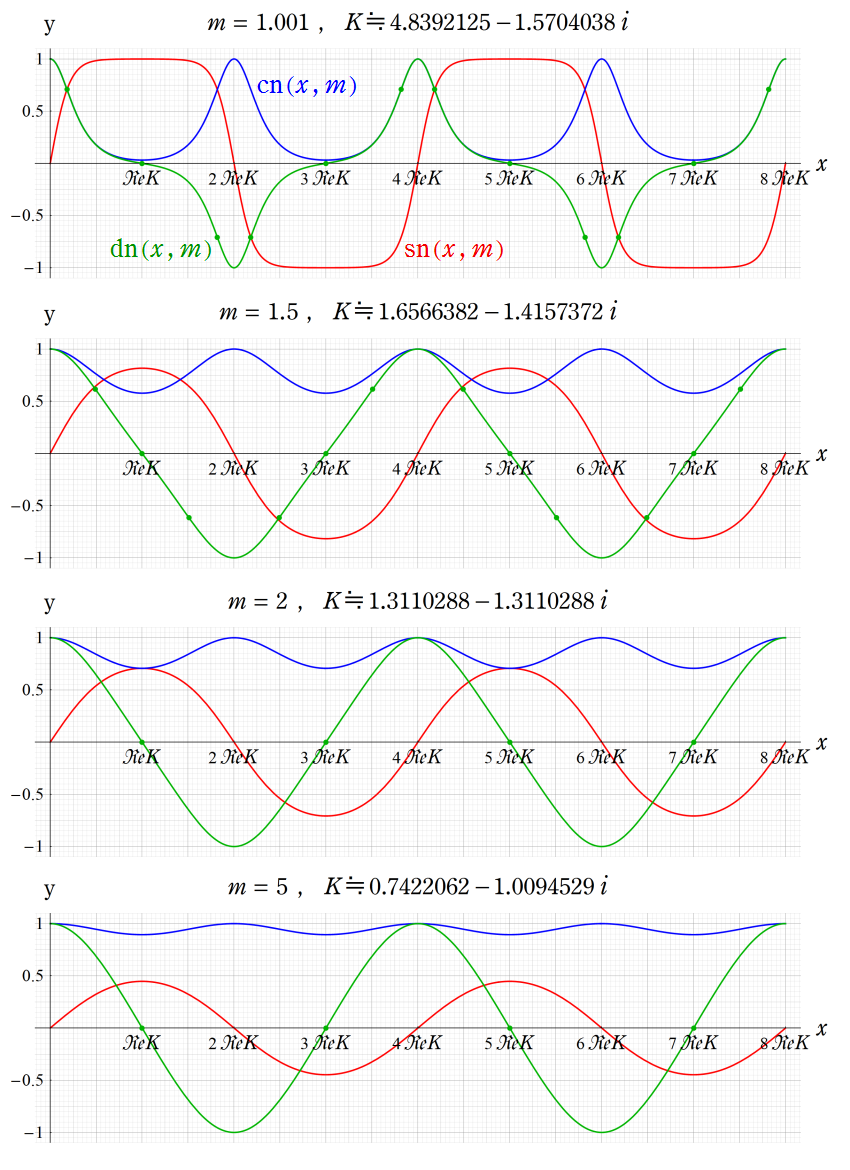
③ m>1の場合。曲線上の点はdn(x, m)の変曲点であり、1<m<2でその個数が増える。
(なおm>1の場合、Jacobi の楕円関数は実軸上で実数値をとるが、第1種完全楕円積分の値は複素数になる。)
3.超幾何関数
次の二階線形常微分方程式は、3個の確定特異点(0,1,∞)を持つ。これを、(Gauss の)超幾何微分方程式といい、この解を超幾何関数という。
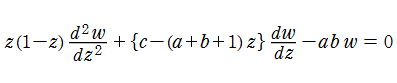
このうち、原点で有限となる基本解は、第1種超幾何関数と呼ばれている。
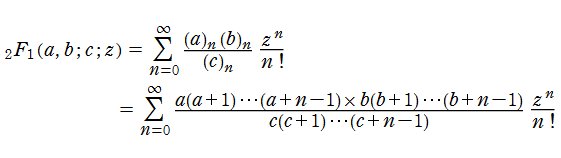
特に、この級数は超幾何級数と呼ばれ、その収束半径は1であるため、実際には、これに線形接続公式等による解析接続を施して定義域を拡張したものが、本来の第1種超幾何関数である。
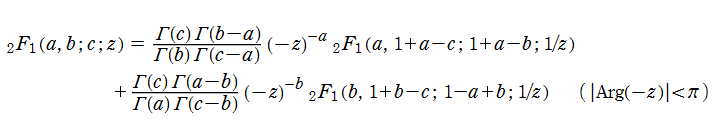
「超幾何級数」という名称は、幾何級数(等比級数)を含む形で一般化した級数という意味を持つ (Hyper geometric series の意訳)。 記号2F1は、Pochhammer 記号が分子に2個、分母に1個あることを示している。 第1種超幾何関数は、aまたはbが負の整数-mのとき、m次の多項式(Jacobi 多項式)となる。
一方、原点で無限大となる、2F1とは線形独立な基本解かある。これは、第2種超幾何関数と呼ばれている。 ただし、a,b,cの値によって発散する場合は極限をとる。この極限によって生じる無限級数は対数項を含む。 なお、第2種超幾何関数の標準的な定義の形、および関数記号は存在していない。
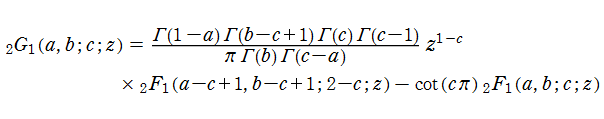
一般に超幾何関数は、複素平面上z=0,1,∞に特異点を持つ無限多価関数であって、通常は-∞~0及び1~+∞に分枝切断線を置く。 前述の二つの基本解は、これらの特異点のうち原点を近似の中心とした場合である。 残り二つの特異点を近似の中心にした場合もそれぞれ考えることができるので、根本的には6種類の基本解(2基本解×3特異点)があり、 さらに6種類の基本解それぞれに対する代数関数因子が4種類あるので、合計24種類の基本解を定め得る。 これらの解の具体的な関数形は、1836年に E. E. Kummer によって求められた。
超幾何微分方程式の一般解は、このような基本解の2個の線形結合式となるが、その係数(関数)はa,b,cの指数関数およびガンマ関数で表わせる。 なお、これよりも高度なクラス (確定特異点が4個以上など) の線形微分方程式になると、一般解の係数の具体的表示は現在でも知られていないか、 または極めて複雑な関数となる。
a,b,cが1だけ互いに異なる3個の超幾何関数は、種々の線形漸化式によって結ばれる。これを「隣接関係式」という。 よく知られた特殊関数の多くで、異なる次数の関数間に漸化式が存在するのは、これらが超幾何関数の特別な場合になっているからである。 隣接関係式は、元々の超幾何関数から異なるa,b,cの超幾何関数が次々と得られるため、非常に便利である。例えば、

のような、特殊値の一群を求めることができる。
超幾何関数の特別な場合として表わされる関数は非常に多く、Jacobi 関数、Gegenbauer 関数、Legendre 陪関数、完全楕円積分などがある。また、(a,b,cが特定条件での)二つの線形独立な超幾何関数の比を逆関数にすると、保型関数が生じる。 超幾何微分方程式の確定特異点のうち1を∞と合流させ、1級の不確定特異点にした微分方程式の解は、合流型超幾何関数と呼ばれ、これの特殊形として表わされる関数も非常に多い。 なお、超幾何関数と直接関係は無いが、超幾何微分方程式の極限として表わされる微分方程式から生じる関数として、 Lamé 関数、Mathieu 関数、回転楕円体波動関数などがある。 これらは超幾何関数よりも高いクラスの関数であるが、比較的整った諸性質(隣接関係式など)を持っていない。 言いかえれば、超幾何関数はそれら「美しい」性質を持つ関数としては、最も高度なものの例である。
超幾何関数は、1748年に L. Euler によって得られた積分表示式
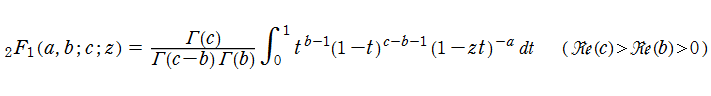
で表わされ、逆にこれをもって超幾何関数の定義とする場合もある。この積分はa,b,cを変数と見た場合、明らかにベータ関数の拡張にもなっている。 超幾何関数は、この他にも様々な積分表示式で表わせることが知られている。
超幾何関数は、単独で物理学等に用いられることは少ない。 むしろ応用上重要な種々の特殊関数どうしの関係、特殊関数の一般論的な側面が問題となる場合に用いられることが多い。
歴史的には、18世紀に Euler が初めて超幾何微分方程式とその解の研究を手掛けた。 19世紀初頭になると、J. C. F. Gauss や N. H. Abel 等によって級数の収束性についての厳密な理論が展開された。 特に 「Gauss の収束判定法」 は超幾何級数のために開発された。
19世紀中葉では複素解析学が整備され、G. F. B. Riemann などの著名な数学者によって、 複素領域で定義された線形常微分方程式の解となる関数の大域的理論や多価関数としての構造が深く研究された。 ここでも超幾何微分方程式および超幾何関数が理論の具体的な雛形であり、発展の原動力となっている。 その後、超幾何関数自体も一般化や多変数化など様々な拡張が考えられ、今なお盛んに研究されている特殊関数の一つになっている。
次の常微分方程式は、ガウスの微分方程式あるいは超幾何微分方程式と呼ばれている。
ここで α, β, γ は複素定数である。
この微分方程式は、x=0,1,∞ において確定特異点を持ち、 それ以外に特異点を持たない。 また各特異点での解はガウスの超幾何関数F(α,β,γ;x)を使って以下の様に表せる事が知られている。
・x=0 での解
・x=1 での解
・x=∞ での解
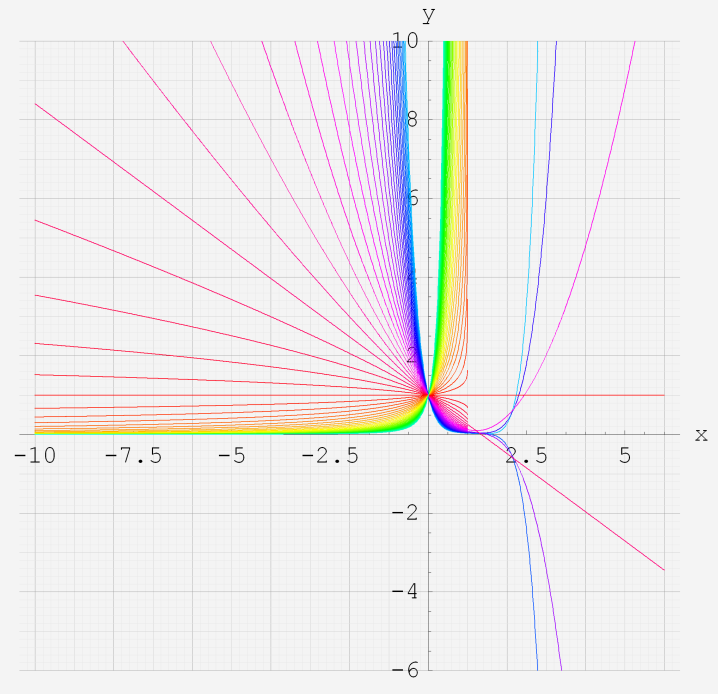
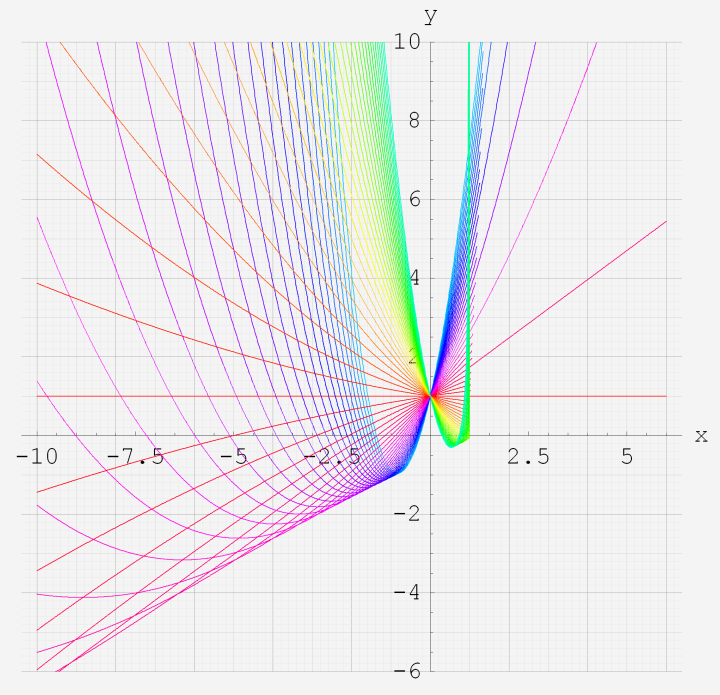
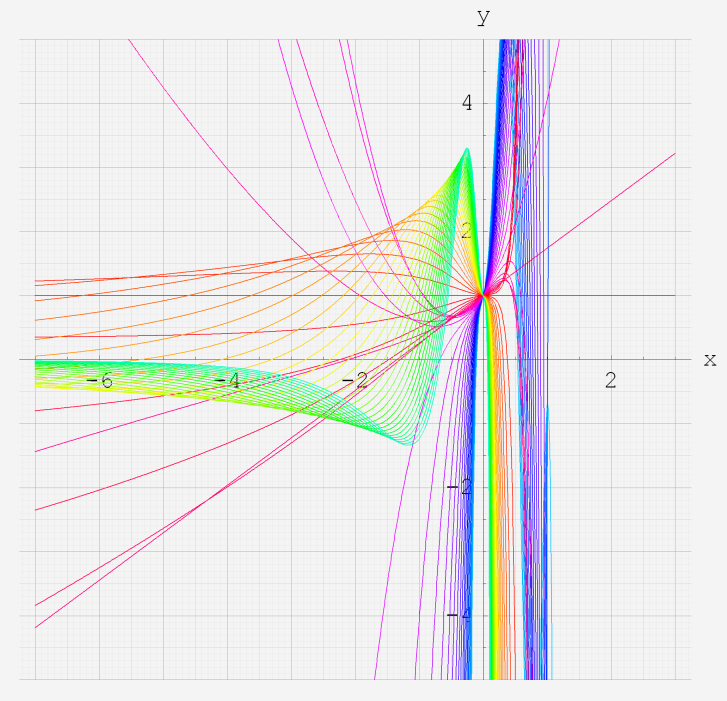
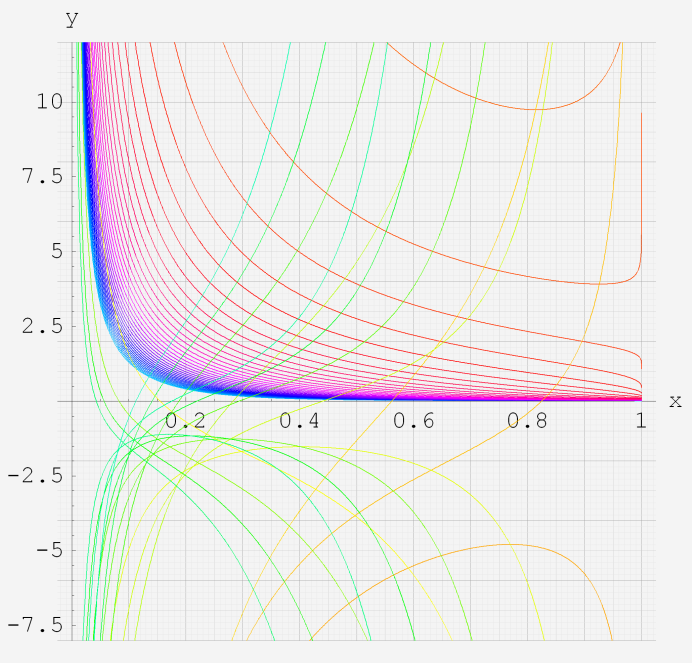
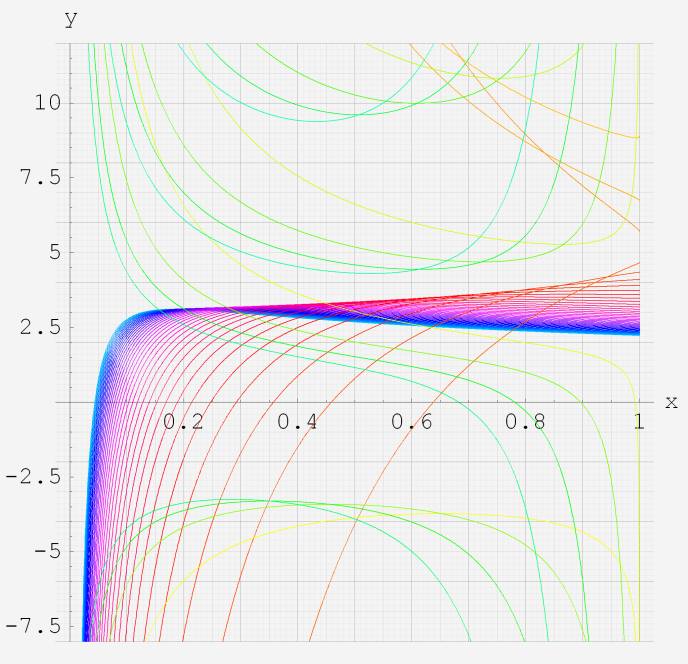
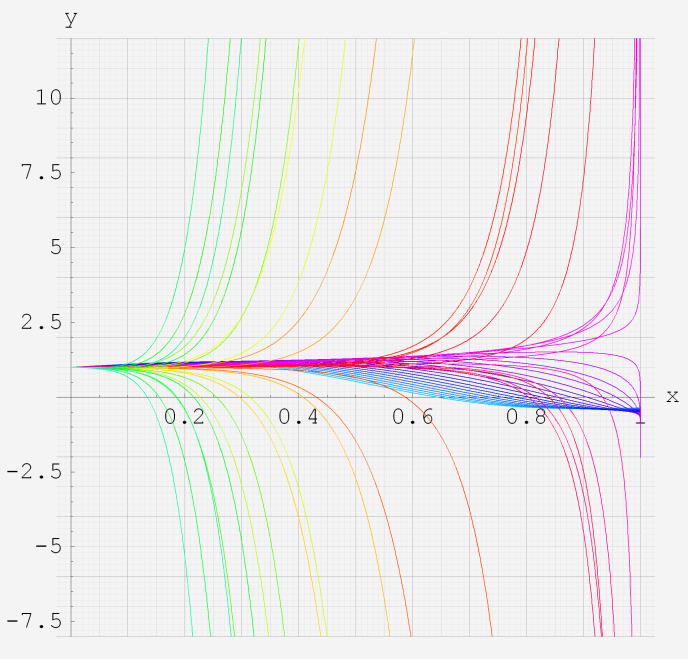
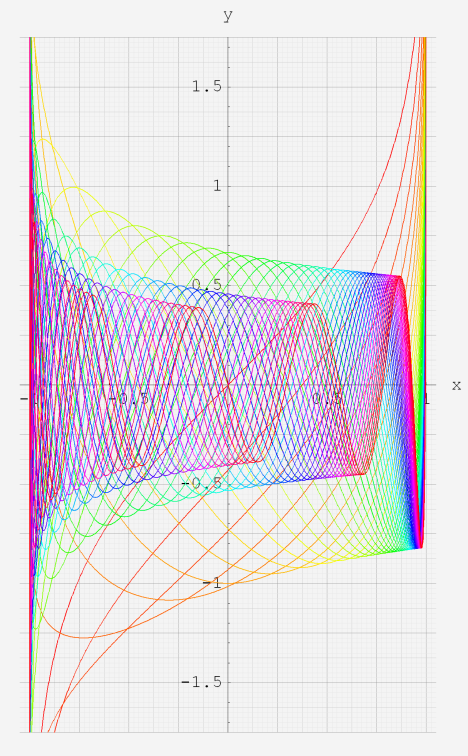
実変数の第1種超幾何関数のグラフ。 順に、
①第1種超幾何関数の記号。②第1種超幾何関数の記号。
③第1種超幾何関数の記号。④第1種超幾何関数の記号。
⑤第1種超幾何関数の記号。⑥第1種超幾何関数の記号。
いずれも、a=-6~6 (+0.2)。
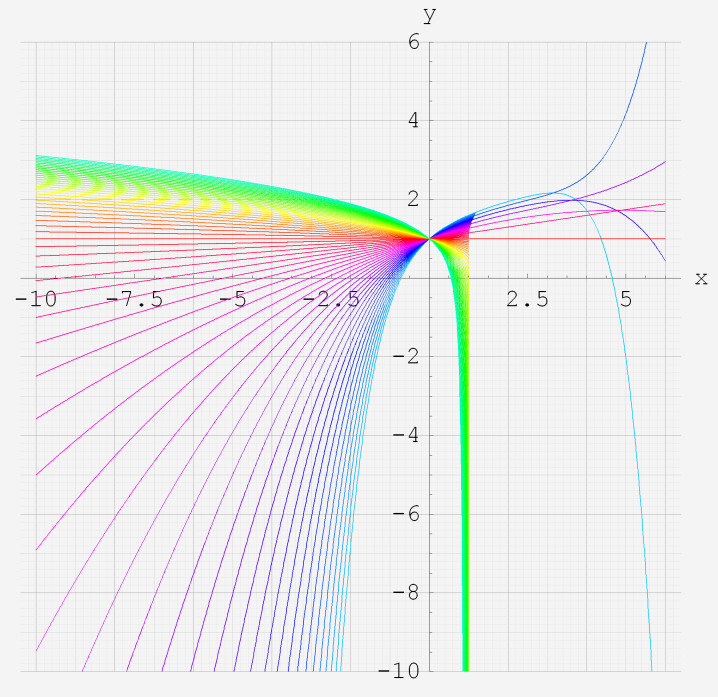
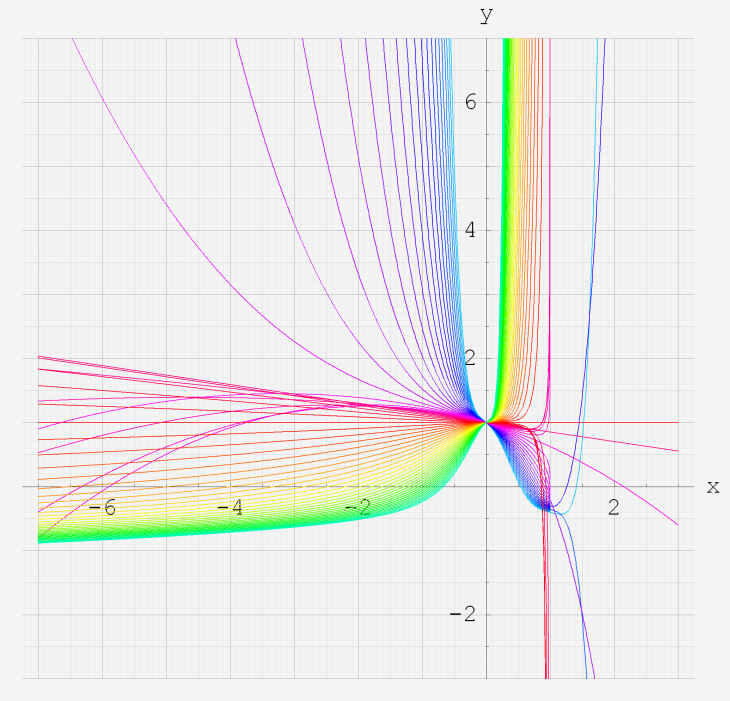
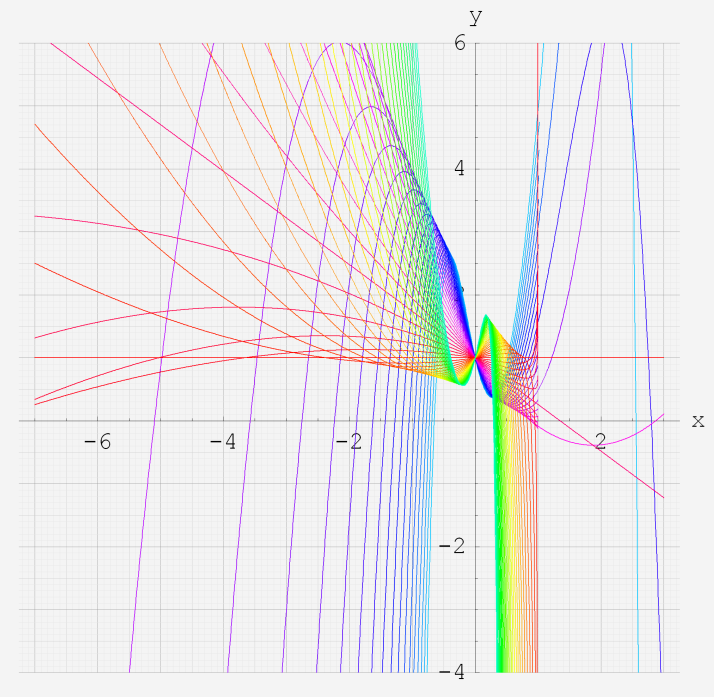
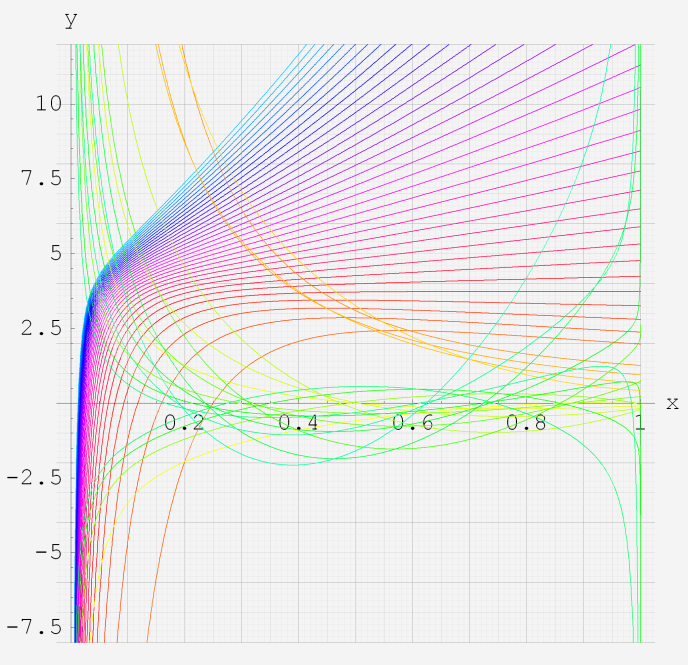
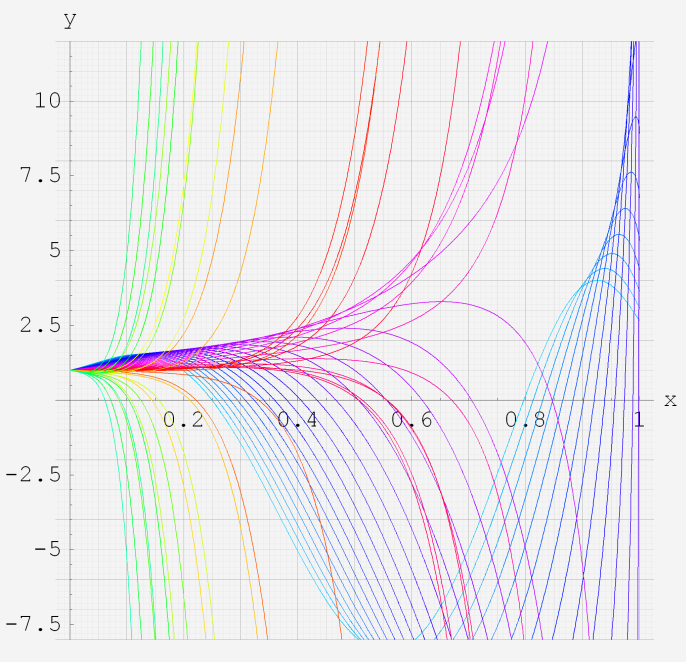
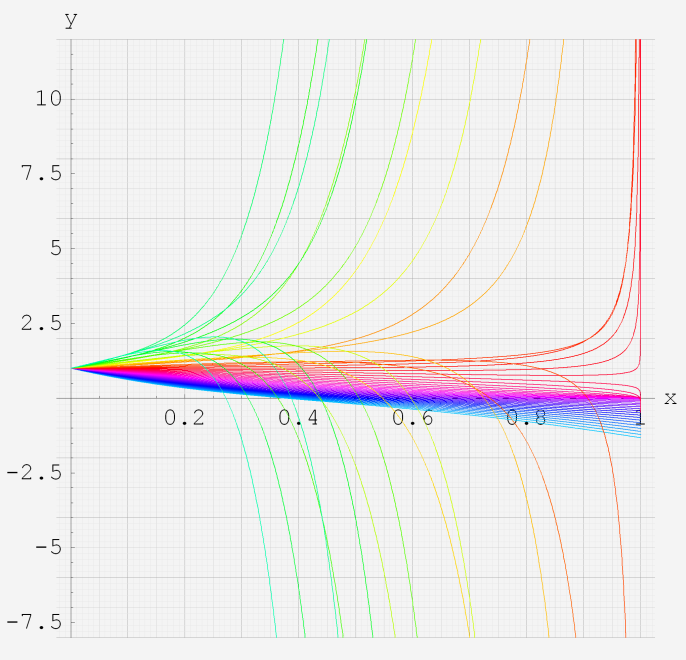
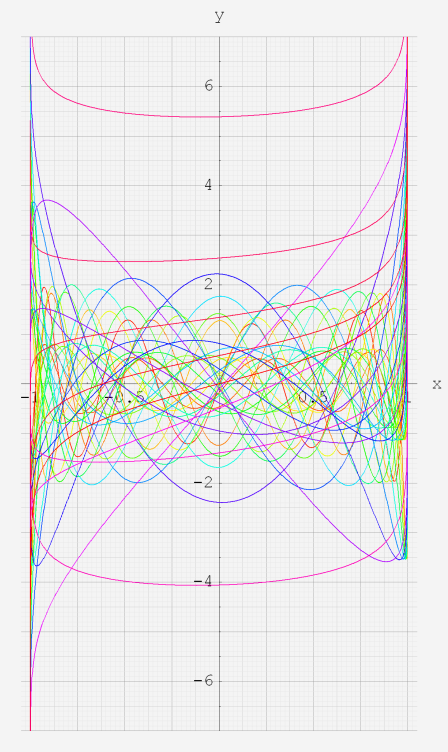
実変数の第2種超幾何関数のグラフ。 順に、
①第2種超幾何関数の記号。②第2種超幾何関数の記号。
③第2種超幾何関数の記号。④第2種超幾何関数の記号。
⑤第2種超幾何関数の記号。⑥第2種超幾何関数の記号。
いずれも、a=-6~6 (+0.2)。
4.球関数(Legendre関数・他)
Legendre の微分方程式は、Laplace の方程式を球座標で変数分離し、角度成分を抽出することから導出される。なお、動径この場合、成分の解は三角関数となる。
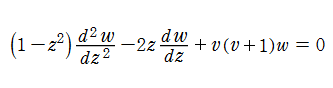
この微分方程式は、線形独立な二つの基本解を持ち、
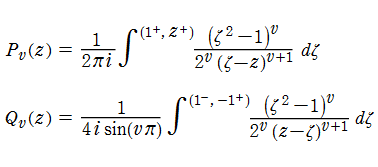
第1種と第2種の Legendre 関数(狭義の球関数)が得られる。 この時、第1種の Legendre 関数は、次数vが非負整数nの場合、次の Rodrigues 公式で表示され、多項式に還元される。
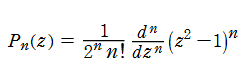
これは Legendre 多項式と呼ばれ、応用上重要とされ、その性質として、次の直交性を持つ。 このため任意の関数は、区間区間(-1, +1)において Legendre 多項式の無限級数に展開可能である。
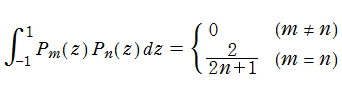
また第2種の Legendre 関数も、次数vが非負整数nのときは、対数関数と多項式を組み合わせたものに還元される。 なお、v次の Legendre 関数は、線形漸化式によって、v-1次及びv-2次の Legendre 関数で表わせる。その際、第2種は第1種と全く同じ形の漸化式で表わされる。
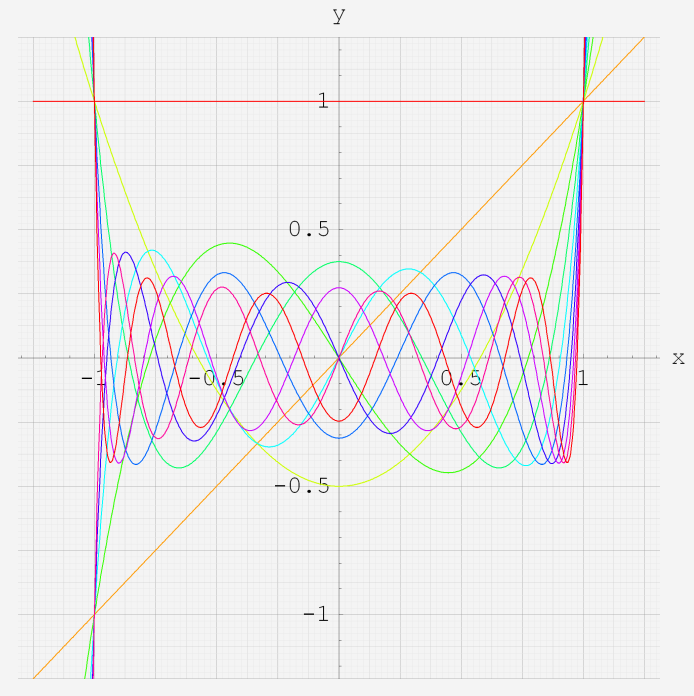
実変数の第1種 Legendre 関数のグラフ。
①最も出現頻度が高い「Legendre 多項式」v=0~10 (+1)の場合。②実数次v=-0.4~10 (+0.2)。
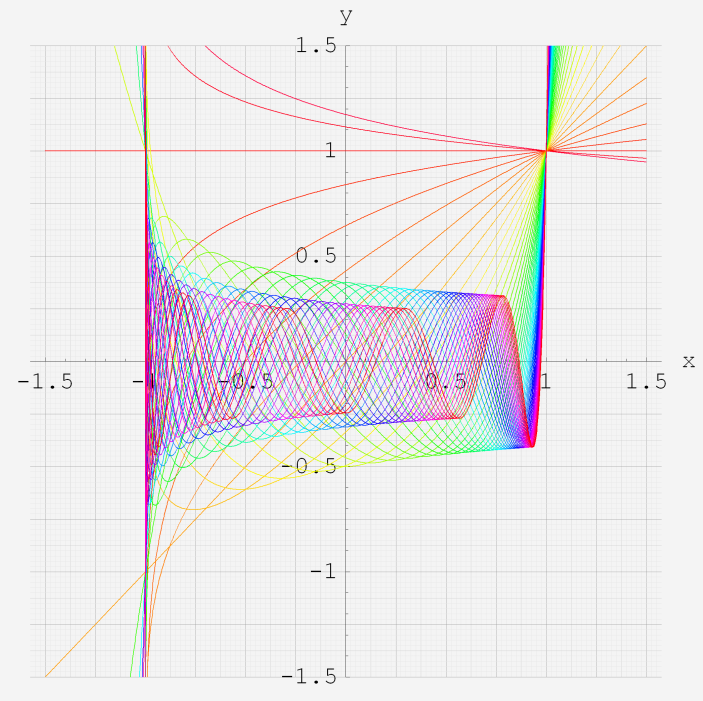
実変数の第2種 Legendre 関数のグラフ。
①最も出現頻度が高い整数次v=0~10 (+1)の場合。②実数次v=0~10 (+0.2)。
③実数次v=-10~0 (+0.2)。
5.円柱関数(Bessel関数・他)
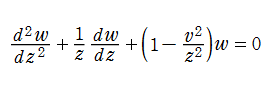
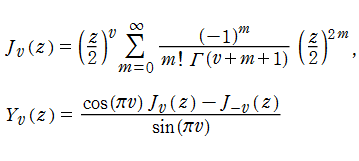
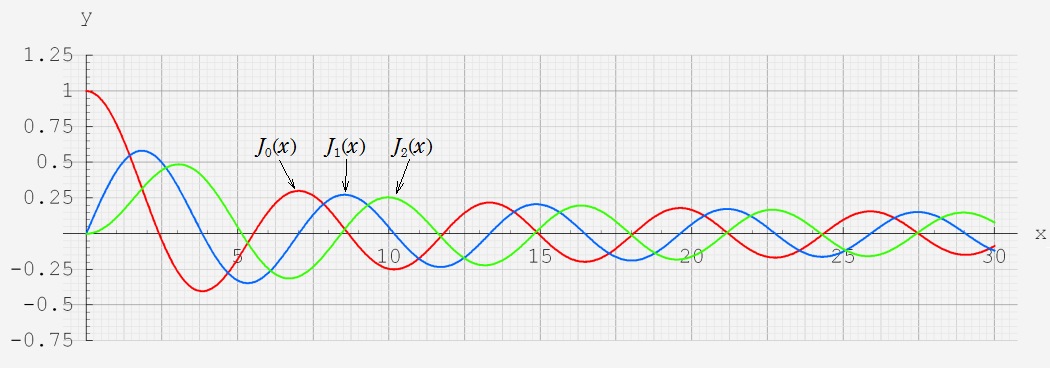
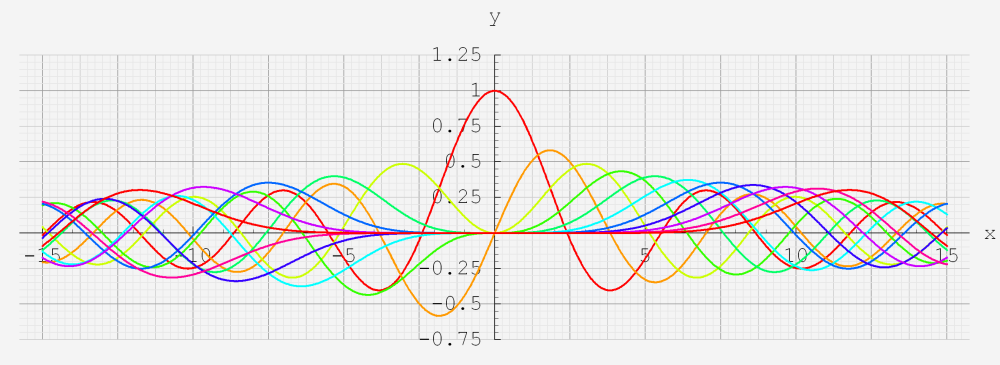
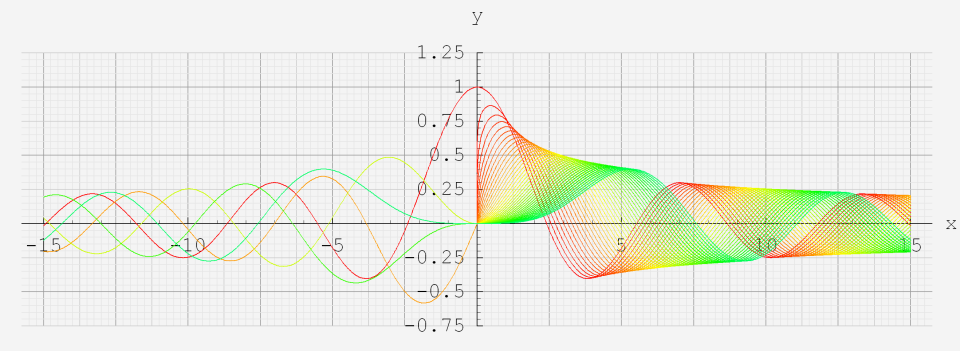
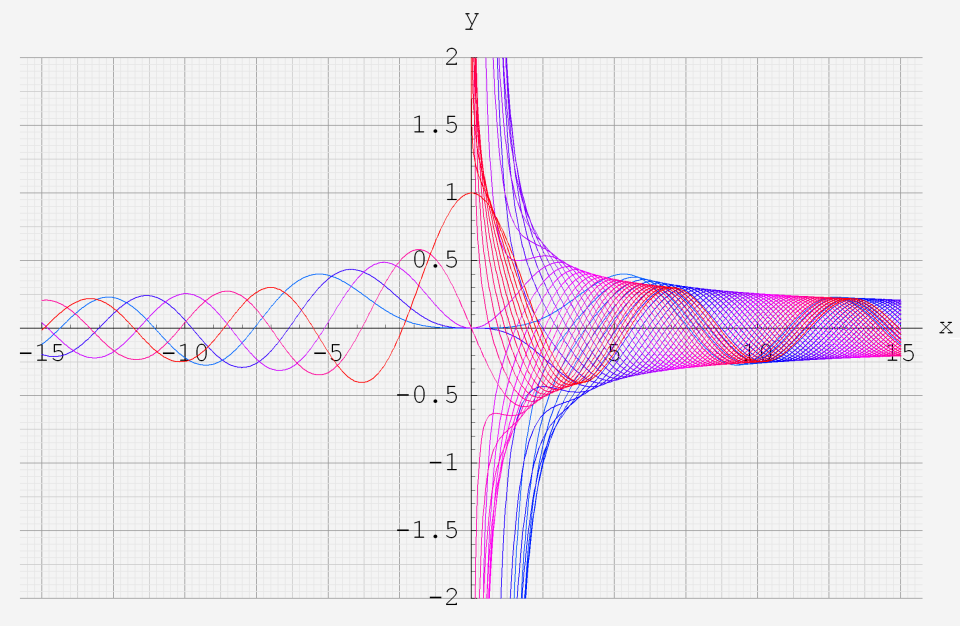
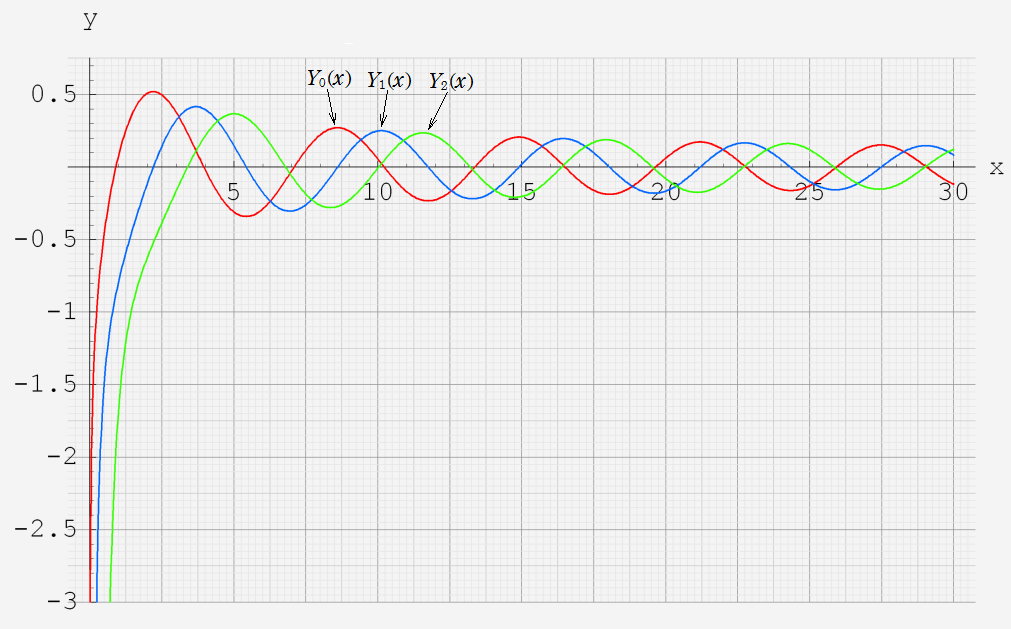
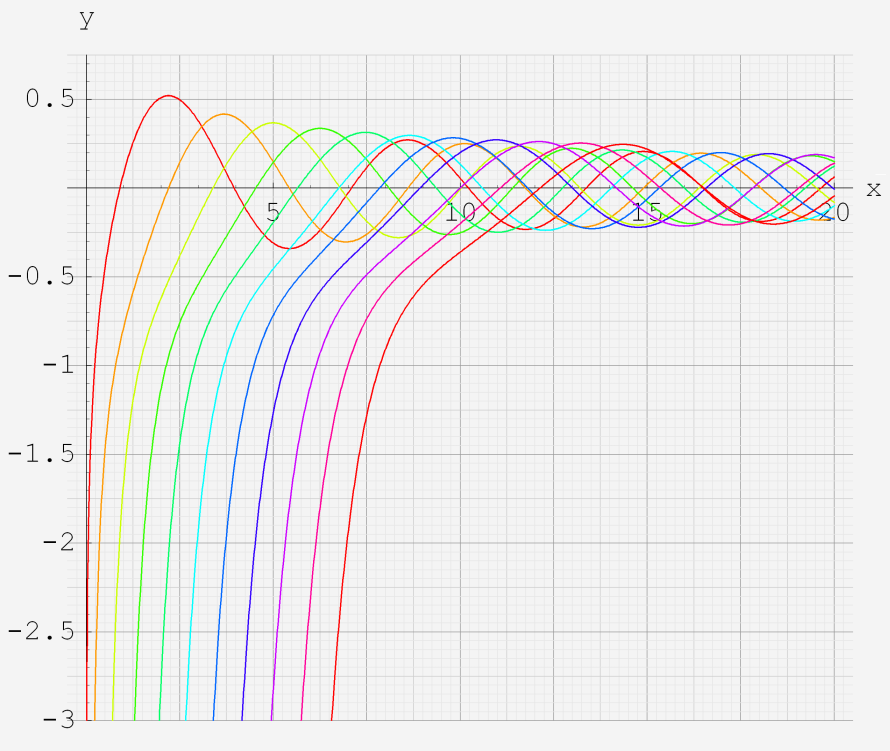
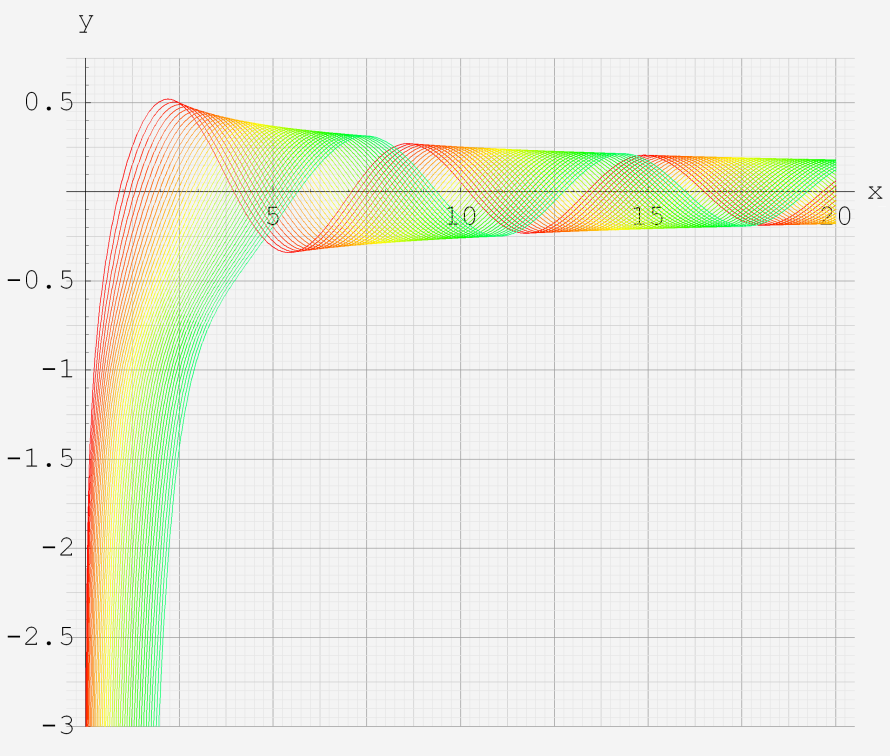
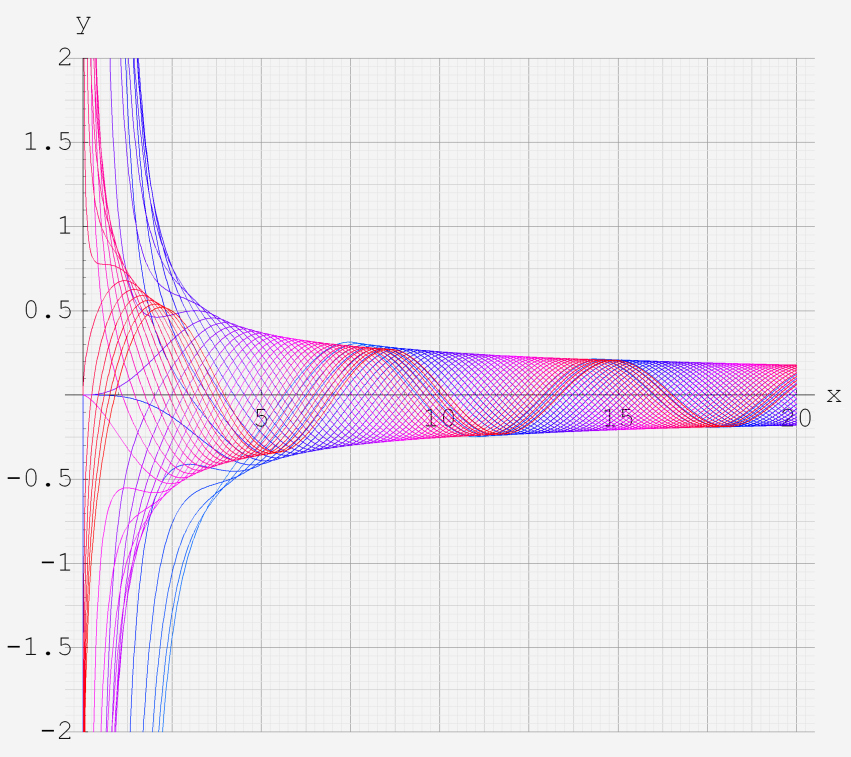
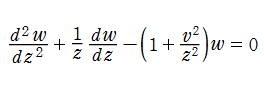
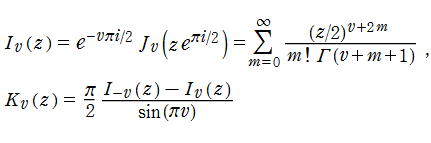
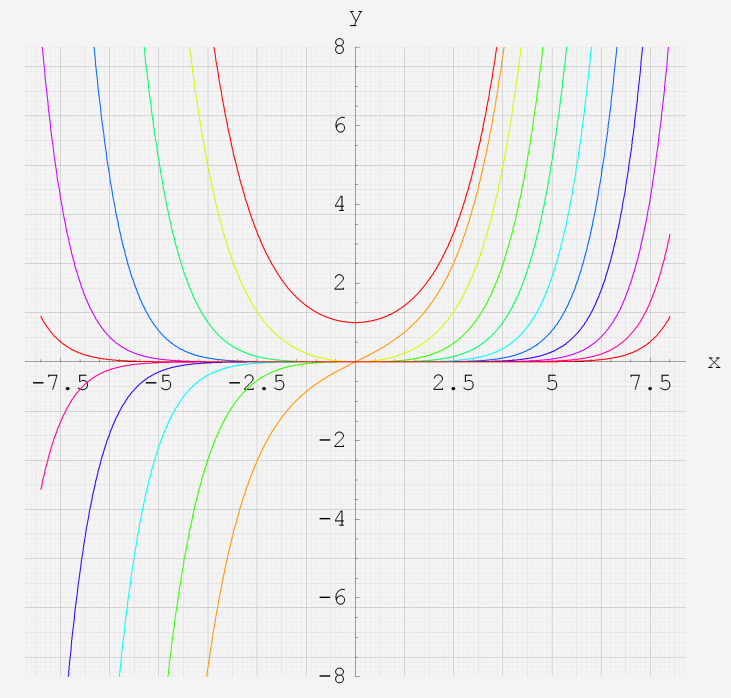
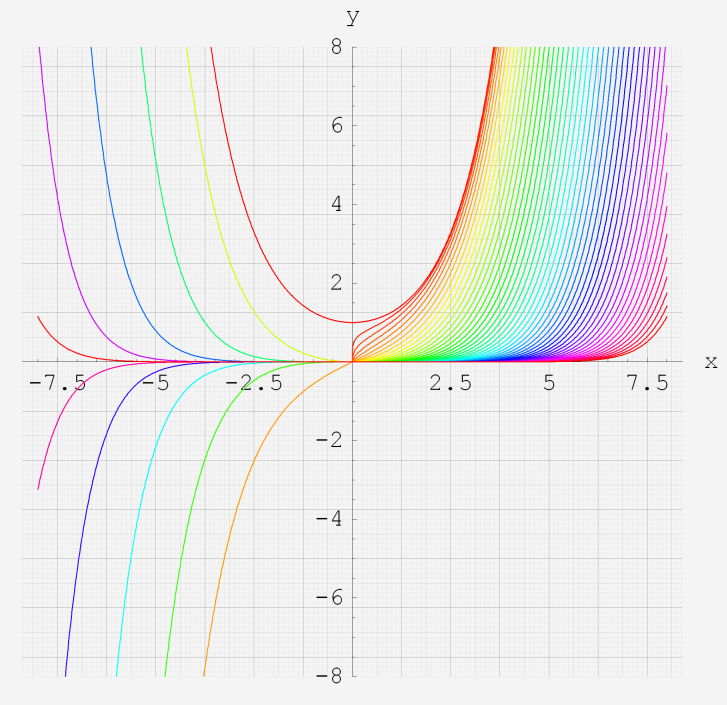
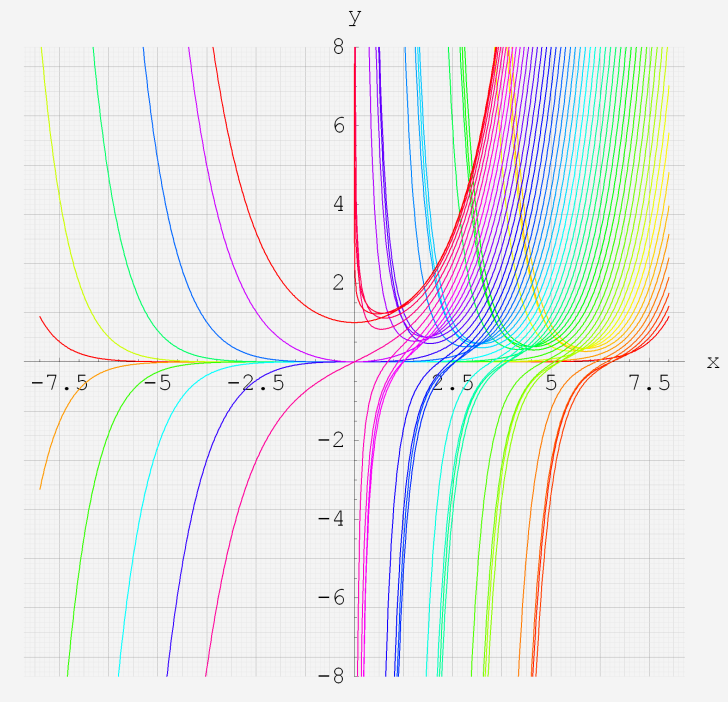
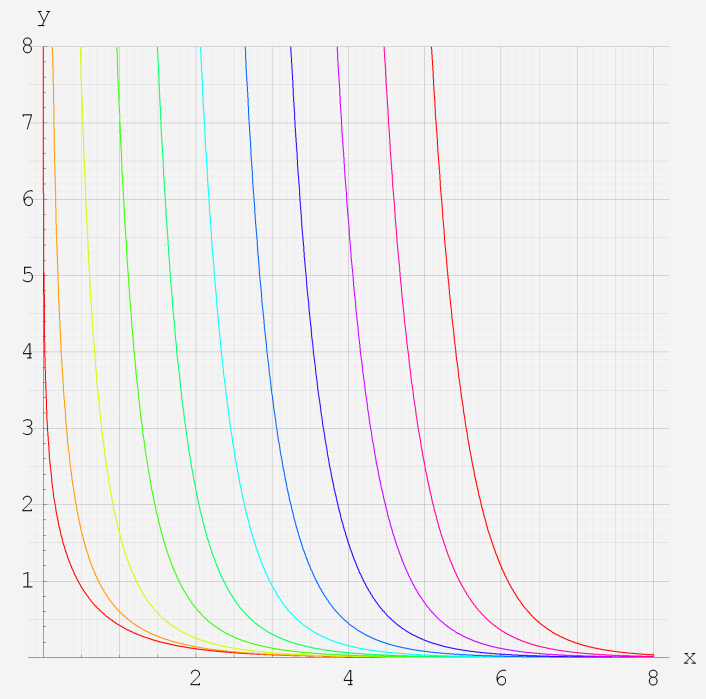
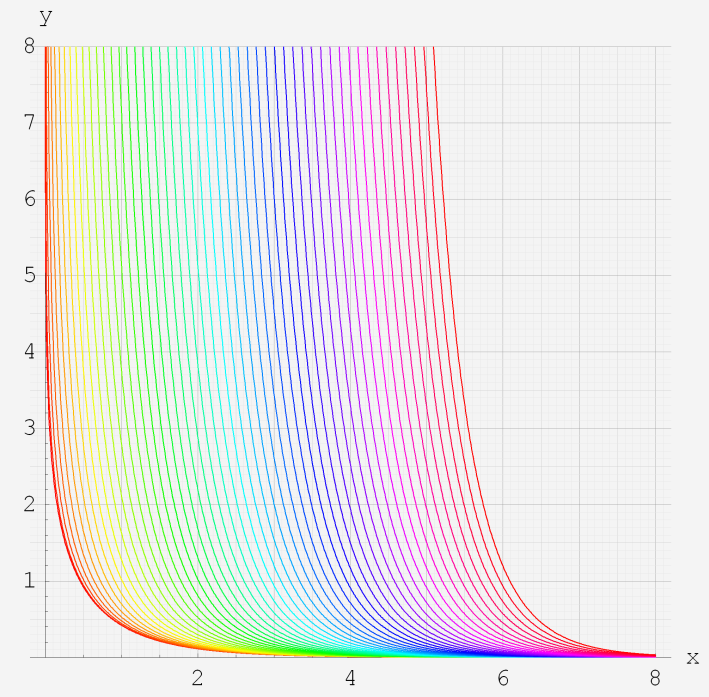
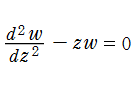
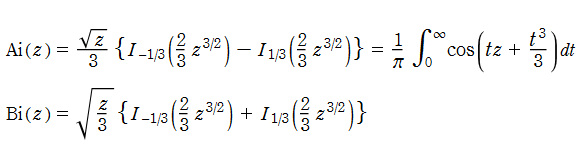
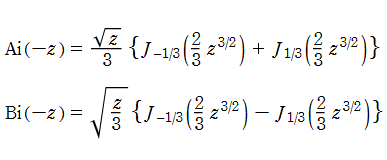
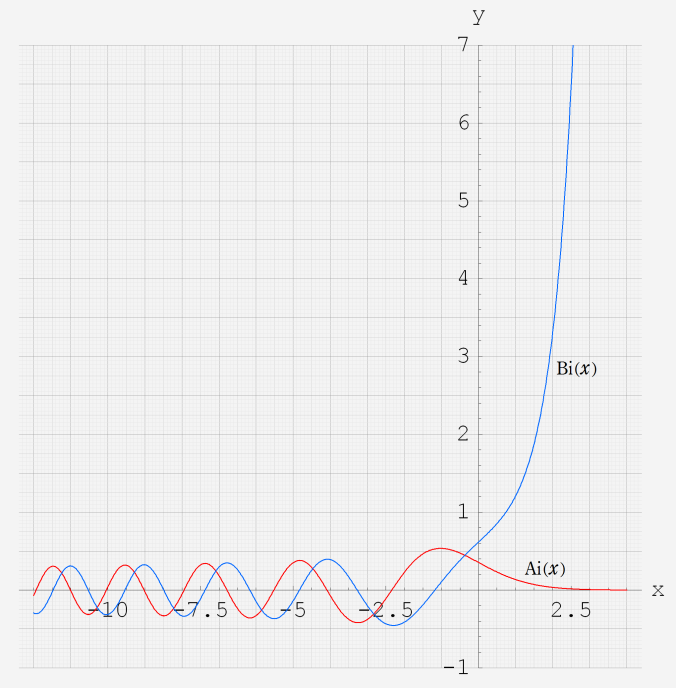
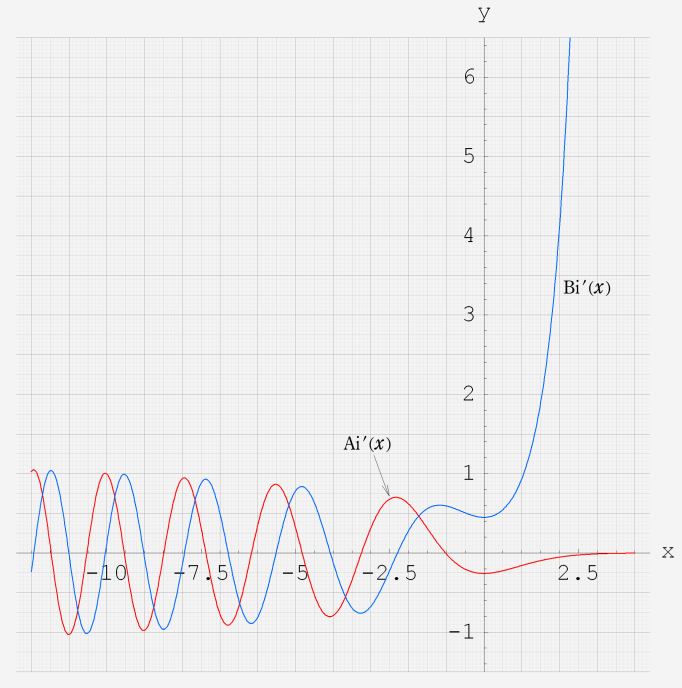
なお、Airy 関数は、純粋数学で広く用いられるほか、物理学では電磁気学、量子力学の境界値問題などで出現する。
6.楕円体関数(Mathieu関数・他)
Helmholtz方程式を楕円柱座標で変数分離すると、楕円成分と双曲線成分の満たす微分方程式が得られ、それぞれ Mathieuの微分方程式の形となる。
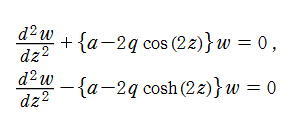
また、Mathieu の微分方程式は、z→arccos(z)なる変換によって、代数的なMathieuの微分方程式に変形できる。
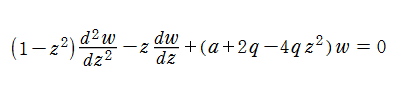
Mathieu の微分方程式は、より一般的な Hill の微分方程式(2階の線形常微分方程式)の特別な場合である。
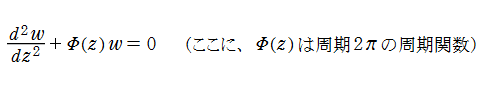
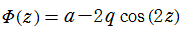
に置き換える。この時、qは与えられた定数、aを適当な値(固有値)に選び、定数0でない周期解が存在するならば、その周期解はMathieu関数または楕円柱関数と呼ばれる。
さらに、aを適当な値(固有値)にとると、二つの基本解の一方が周期2π(またはπ)の周期関数になる。 この周期関数解は、極限q→0、a→n2(nは整数)の時、cos(nz)に近づく解とsin(nz)に近づく解に分類でき、 cen(z,q)およびsen(z,q)と表記する。これを (整数次の)第1種Mathieu関数という。 なお、これを 楕円余弦関数および楕円正弦関数と呼ぶこともある。
つまり、q=0の時、a=n2[nが0または正の整数]が固有値、解の基本系は、cos(nz),sin(nz) である。 また、q→0の時、cos(nz),sin(nz)に収斂するMathieu関数は、それぞれ、
なお、z→±izなる変換によって、n次の変形されたMathieu関数の周期解は、
で表示される。これらは、それぞれ cosh(nz),sinh(nz) に収斂する。
(整数次)第1種 Mathieu 関数は、直交性を有する。
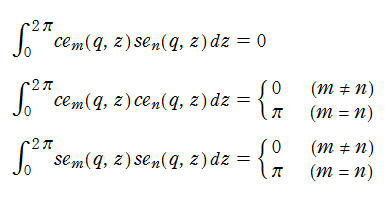
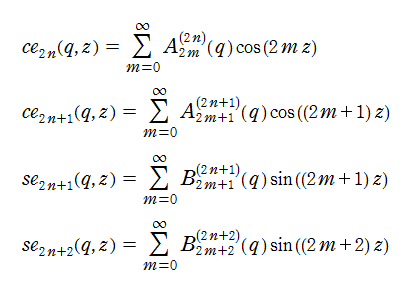
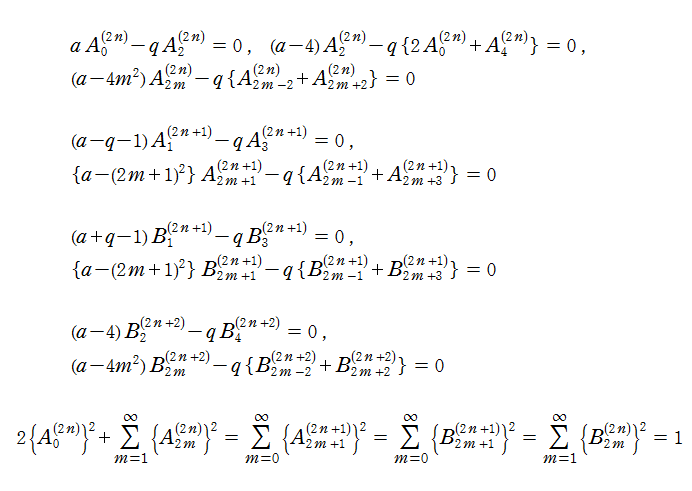
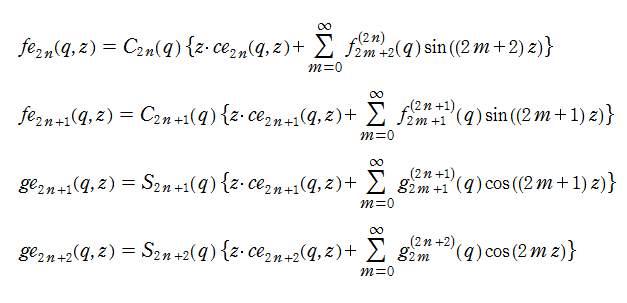
なお、非整数次n=vの Mathieu 関数は、これらと似ているが異なる定義になる。 また固有値aは、vとqの関数として表わされる。このほか、第3種 Mathieu 関数として
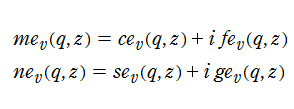
一般に Mathieu 関数は超越整関数のため、無限遠点のほかに特異点を持たない。 代数的な Mathieu の微分方程式の解としての Mathieu 関数は、複素平面上z=±1,∞に特異点を持つ無限多価関数であって、 通常は-∞~-1及び+1~+∞に分枝切断線を置く。つまり、後者の場合の多価性は逆余弦関数に由来しているにすぎない。
Mathieu 関数は楕円柱関数という別名があるとおり、楕円形膜の振動問題のように境界が楕円柱である場合などの物理問題に現れる。 このほかにも電磁波の散乱現象など近年は応用面が増えつつあるが、Bessel 関数などに比べるとずっと少ない。 それは Mathieu 関数の計算が複雑で取り扱いが難しいことにもよる。
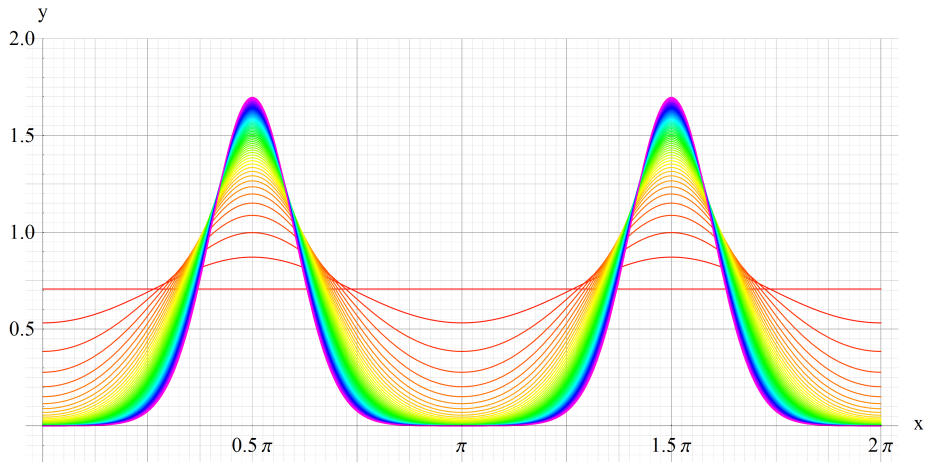
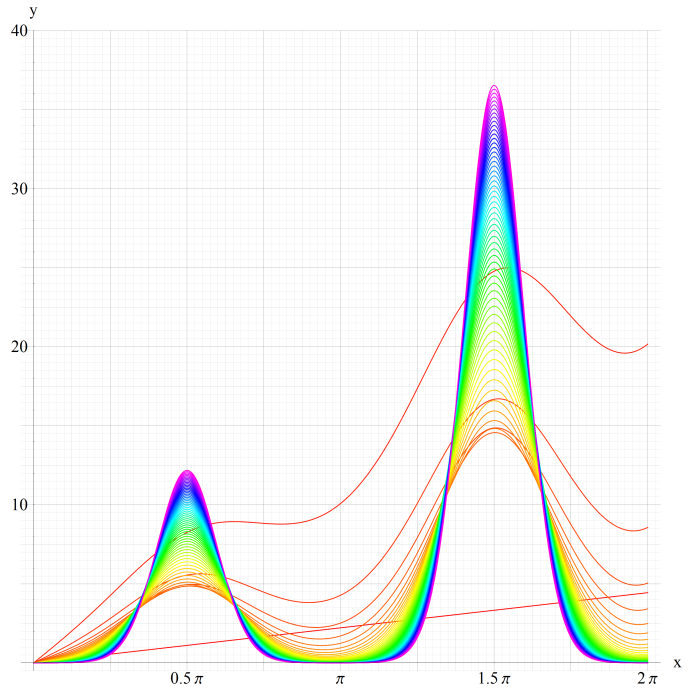
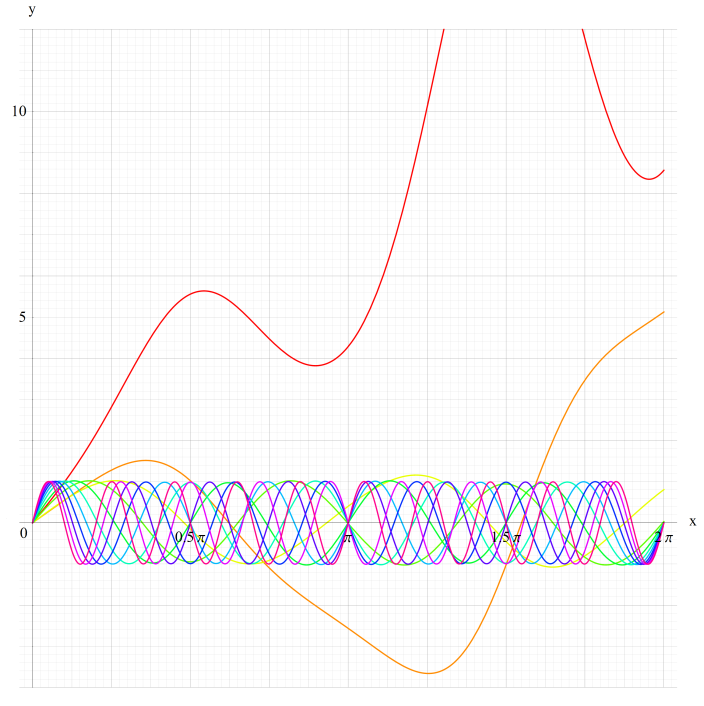
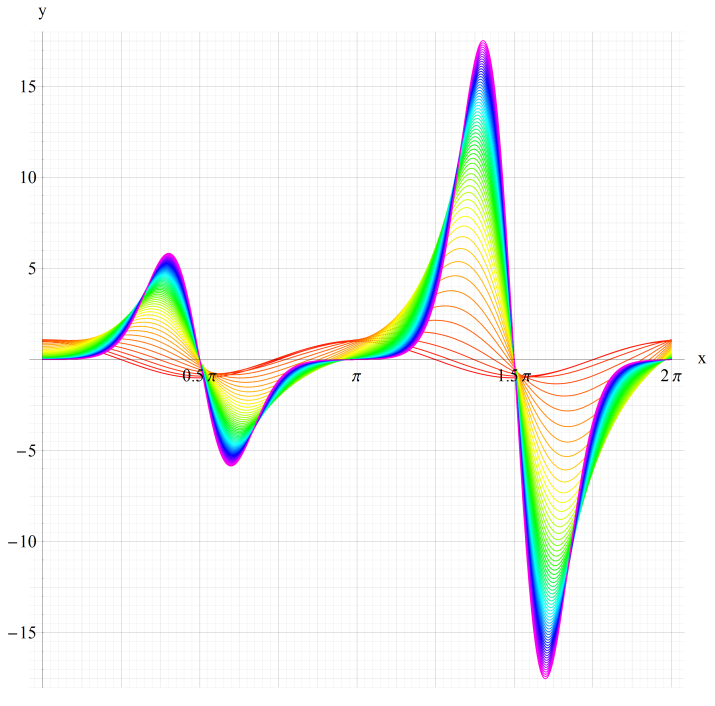
①ce0(q,x)、②ce1(q,x)
③ce2(q,x)、④ce3(q,x)
いずれも q=0~30 (+0.5)
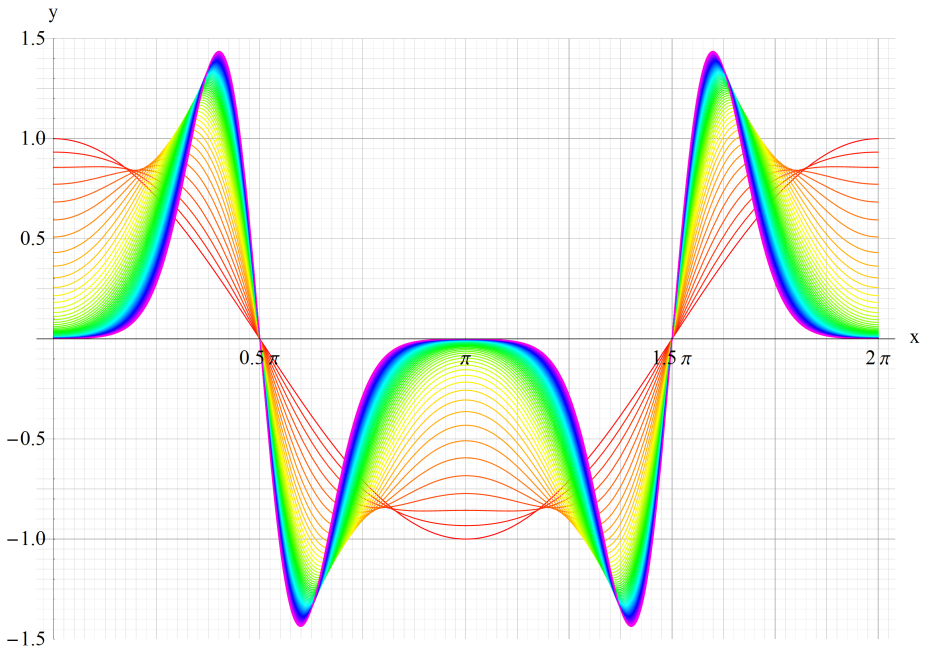
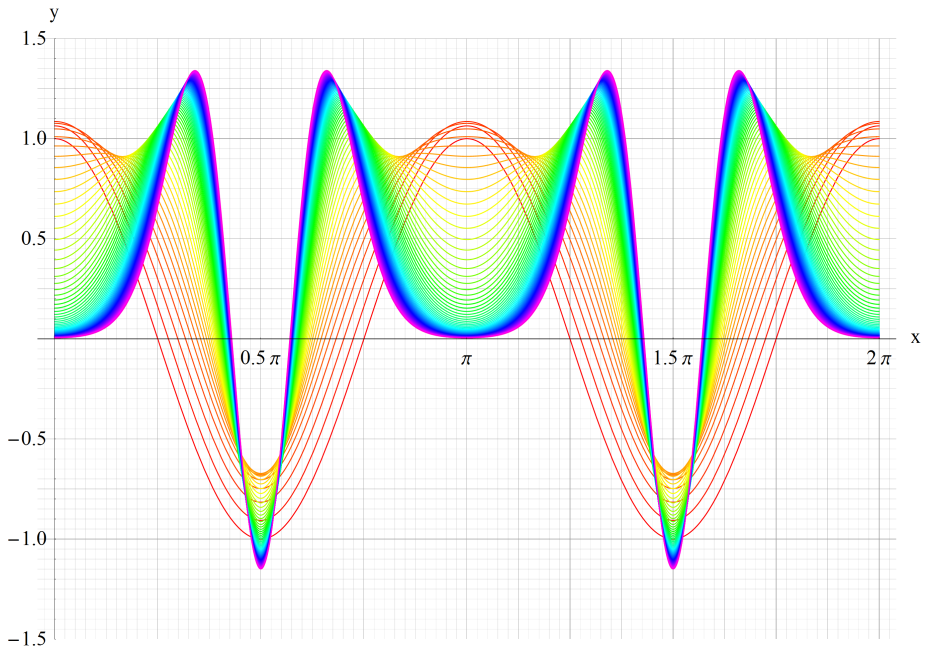
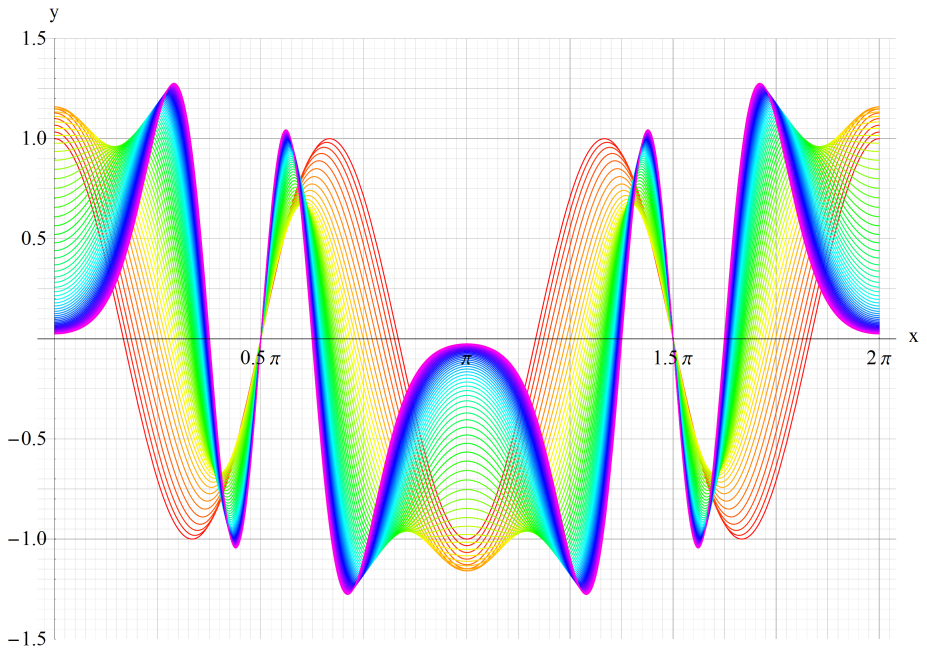
①cen(1,x)、②cen(5,x)、③cen(20,x)
いずれも n=0~10 (+1)
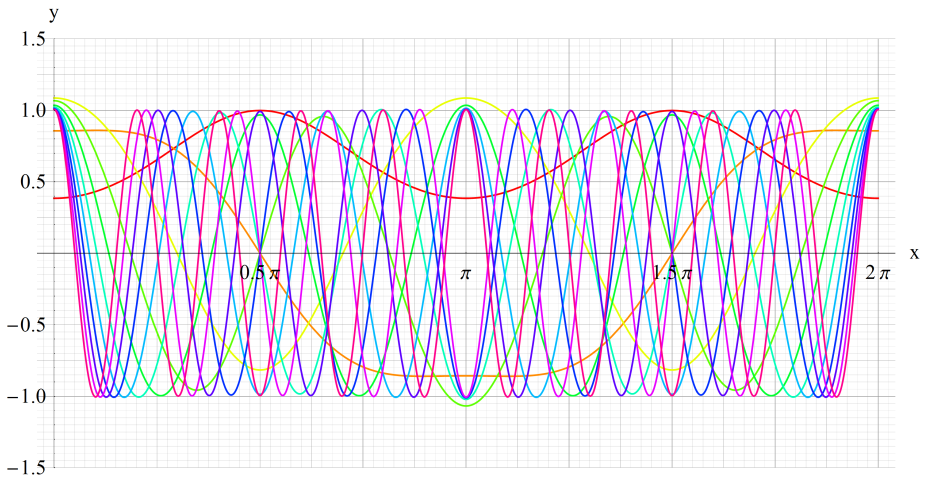
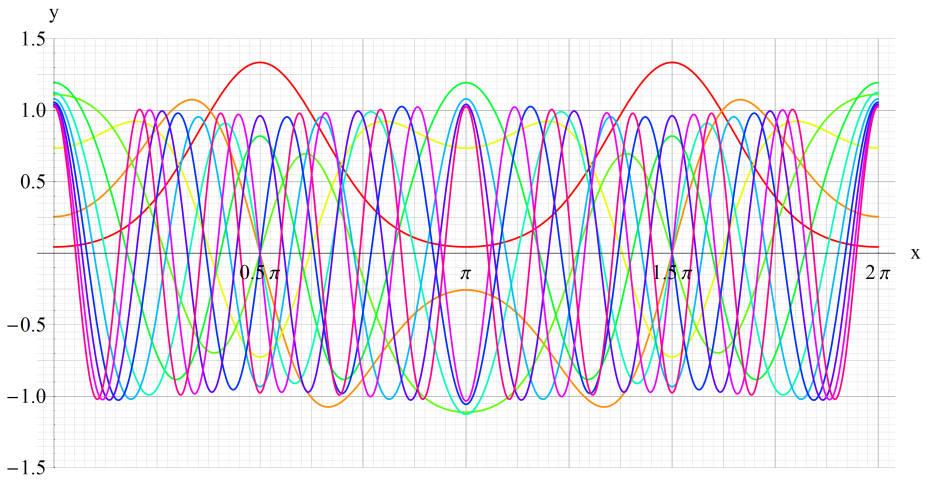
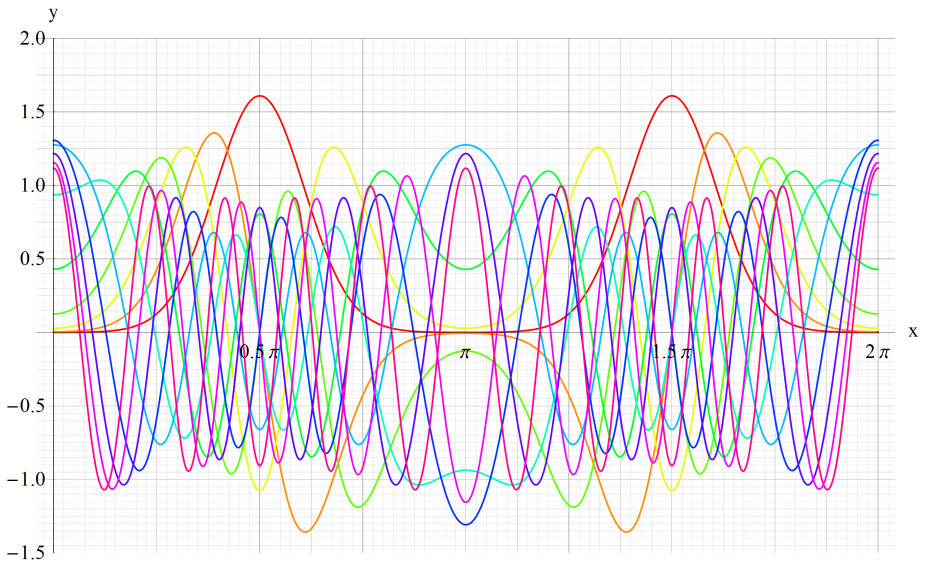
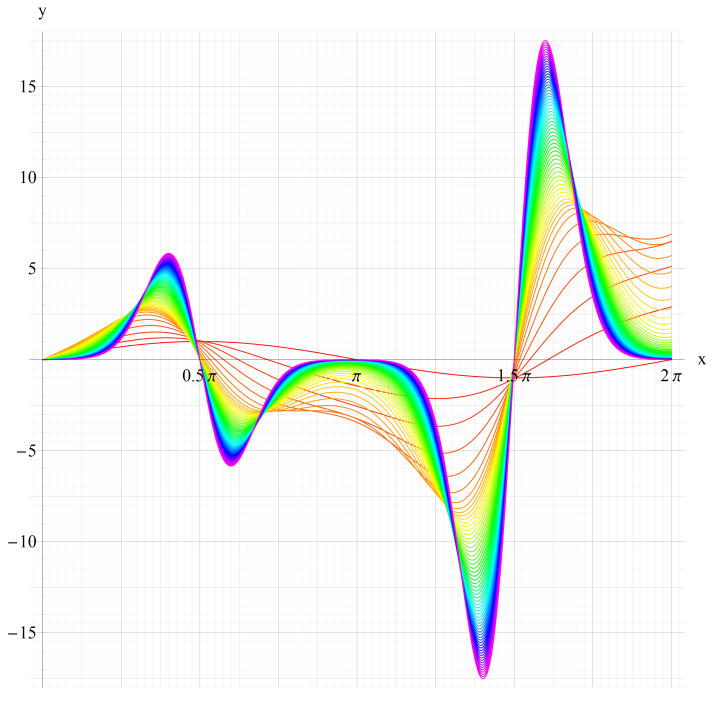
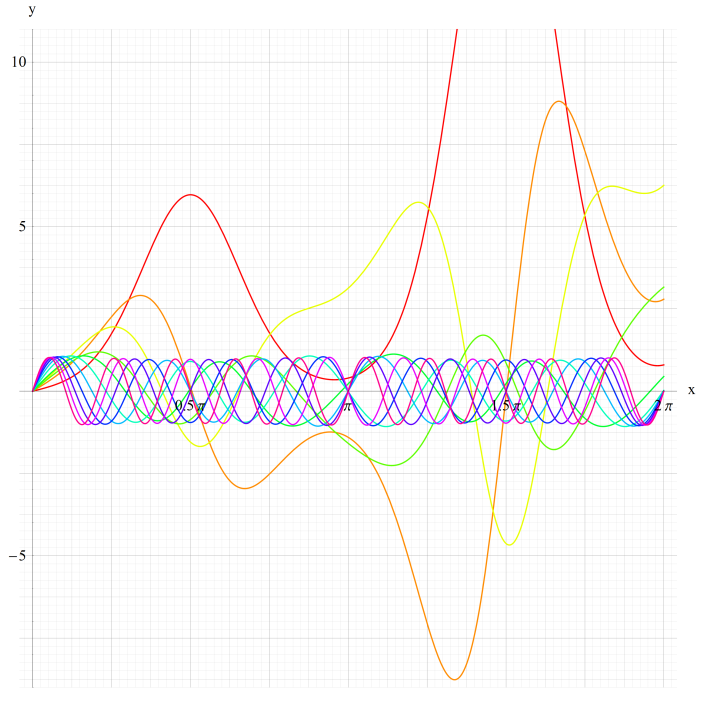
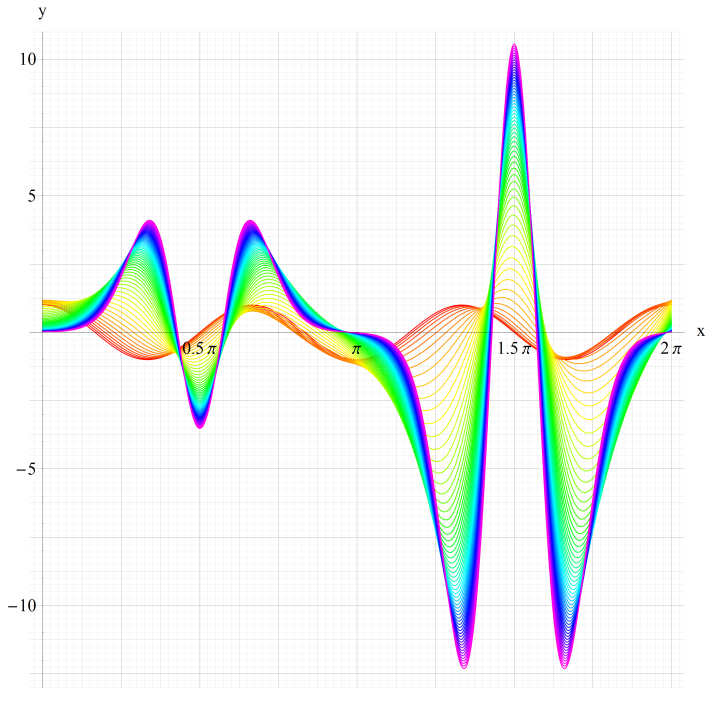
①se1(q,x)、②se2(q,x)
③se3(q,x)、④se4(q,x)
いずれも q=0~30 (+0.5)。
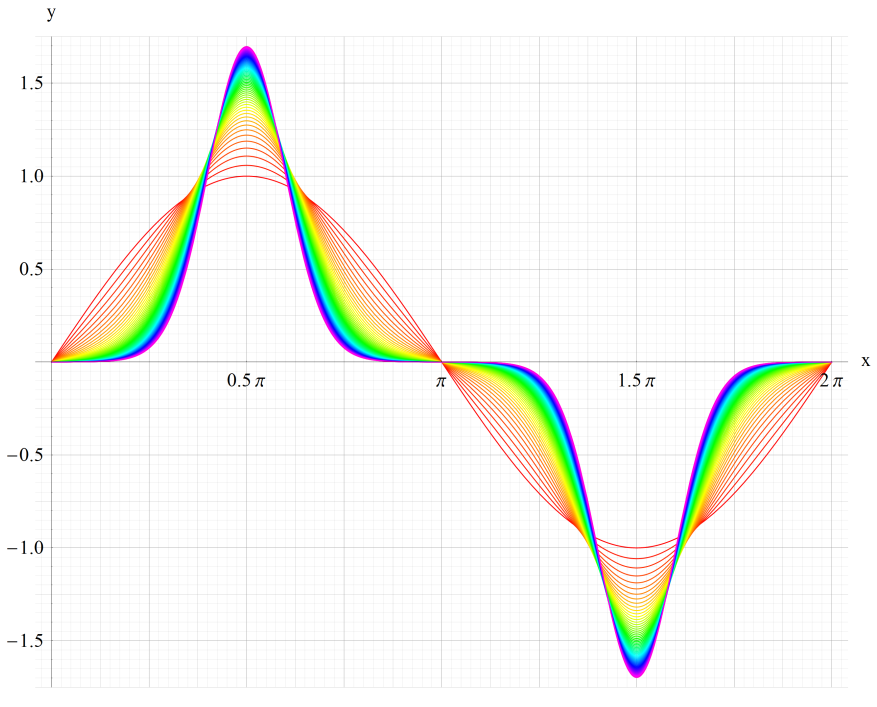
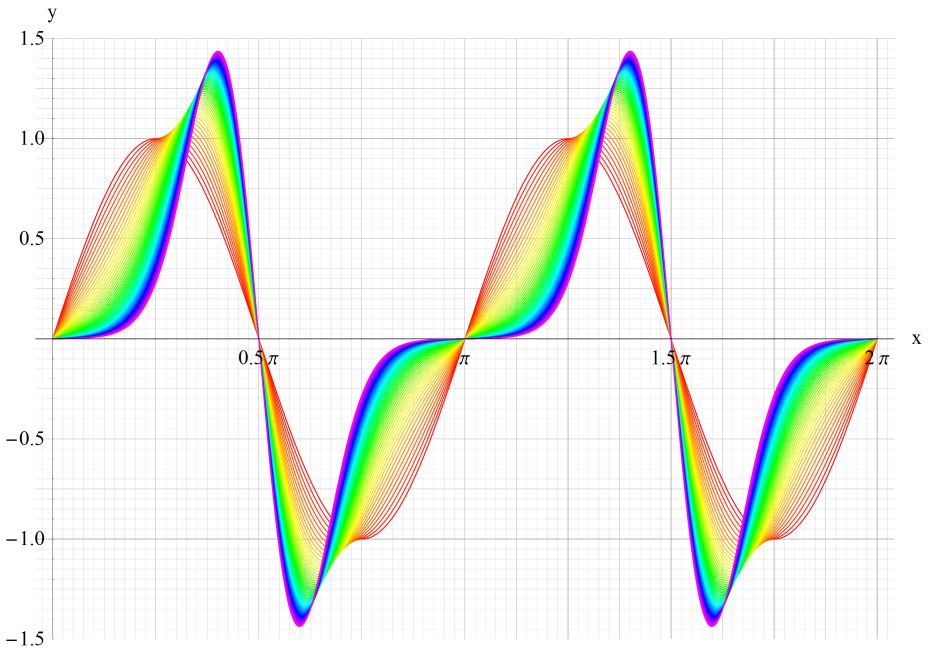
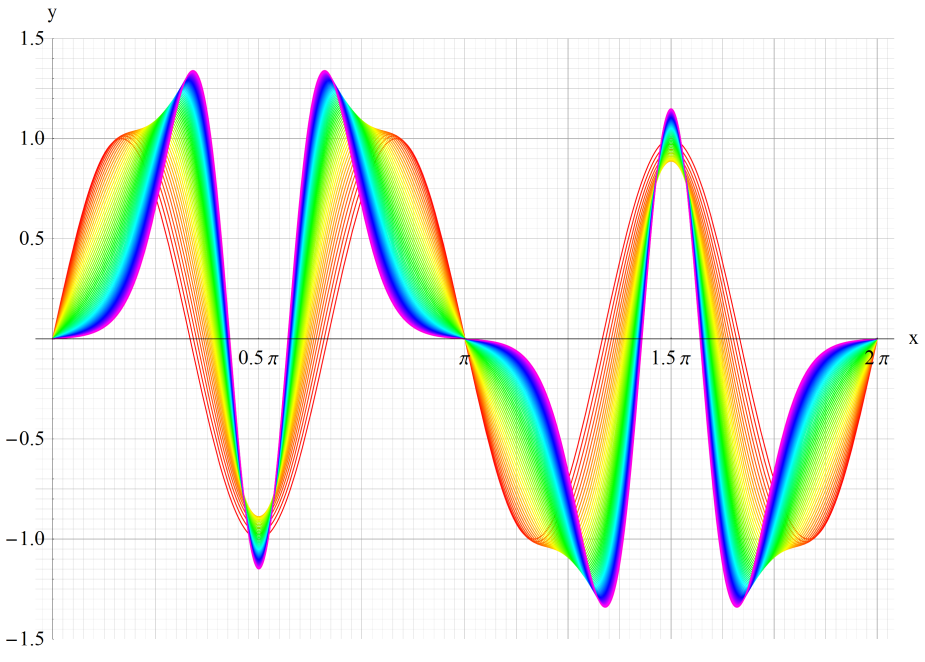
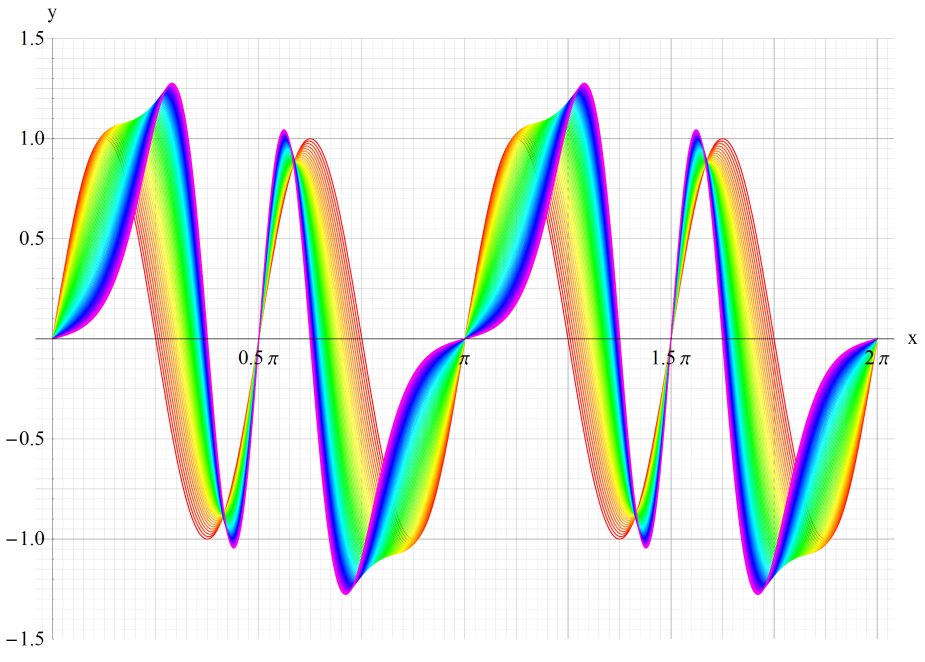
①sen(1,x)、②sen(5,x)、③sen(20,x)
いずれも n=0~10 (+1)。
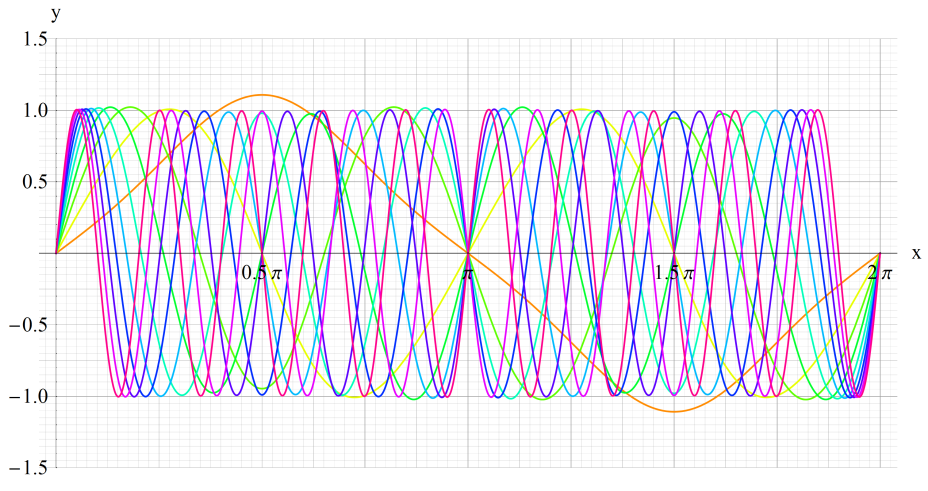
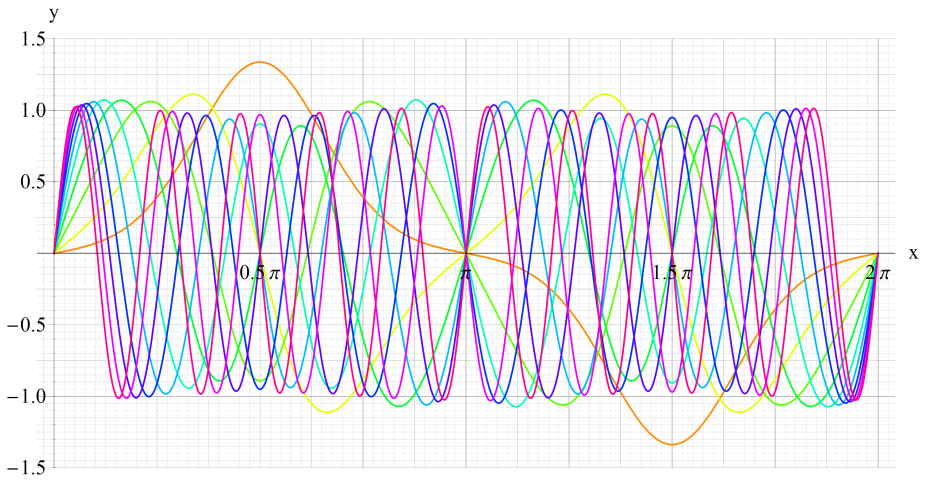
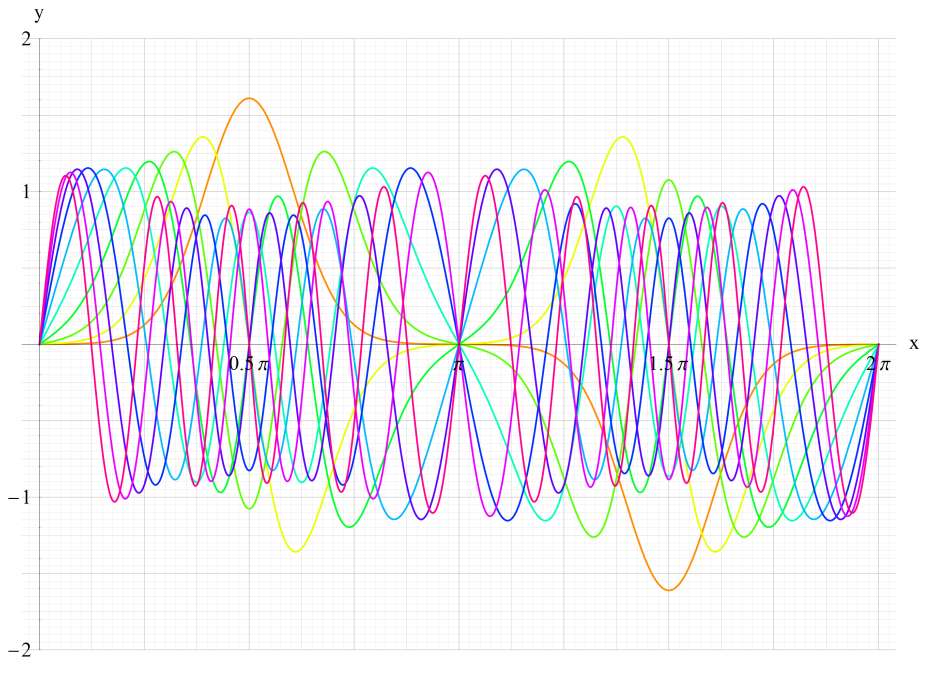
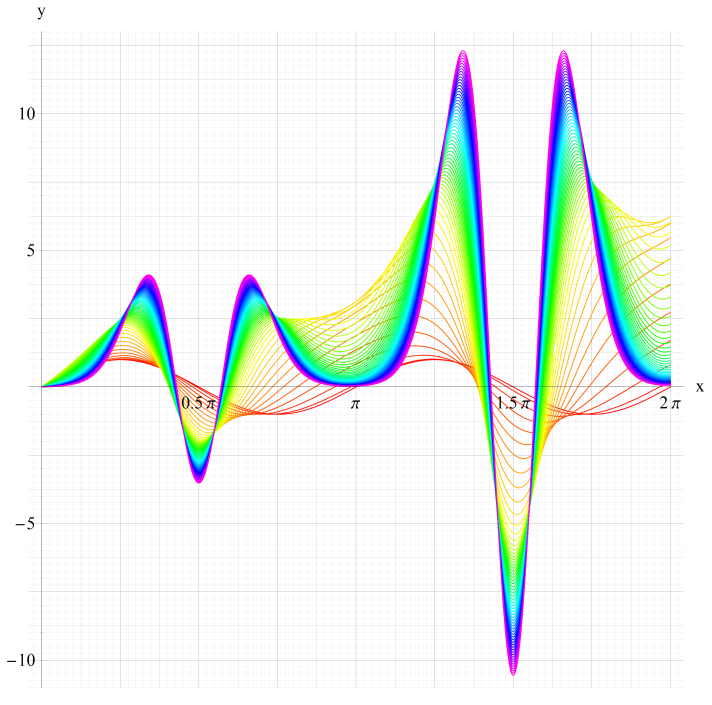
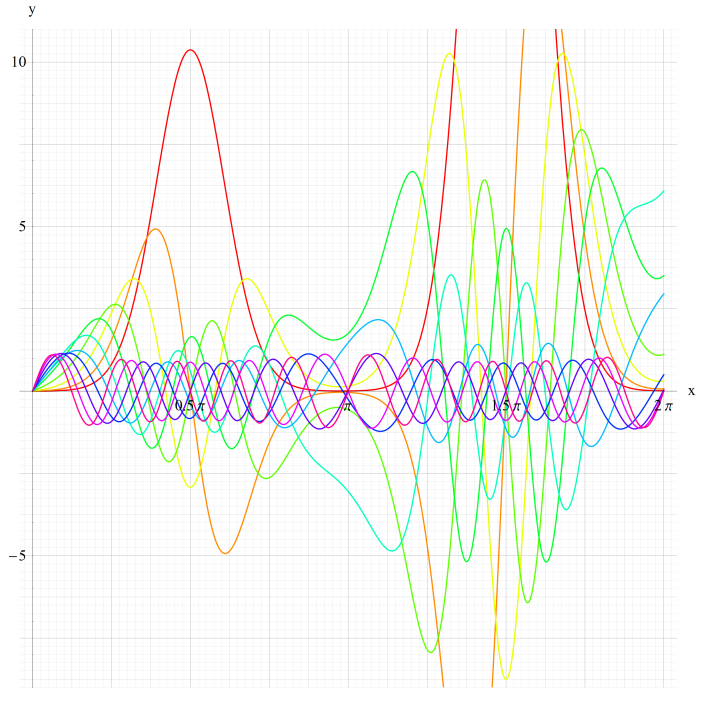
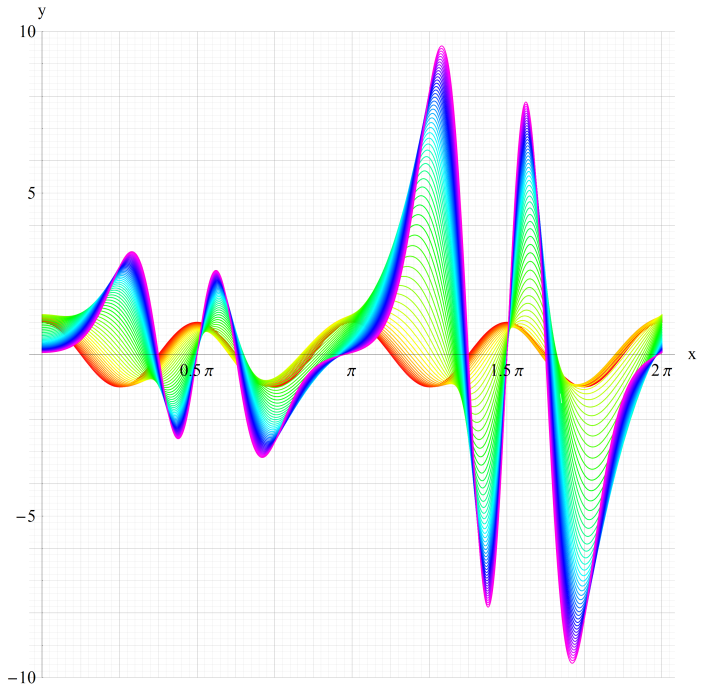
①fe0(q,x)、②fe1(q,x)
③fe2(q,x)、④fe3(q,x)
いずれも q=0~30 (+0.5)。
①fen(1,x)、②fen(5,x)、③fen(20,x)
いずれも n=0~10 (+1)。
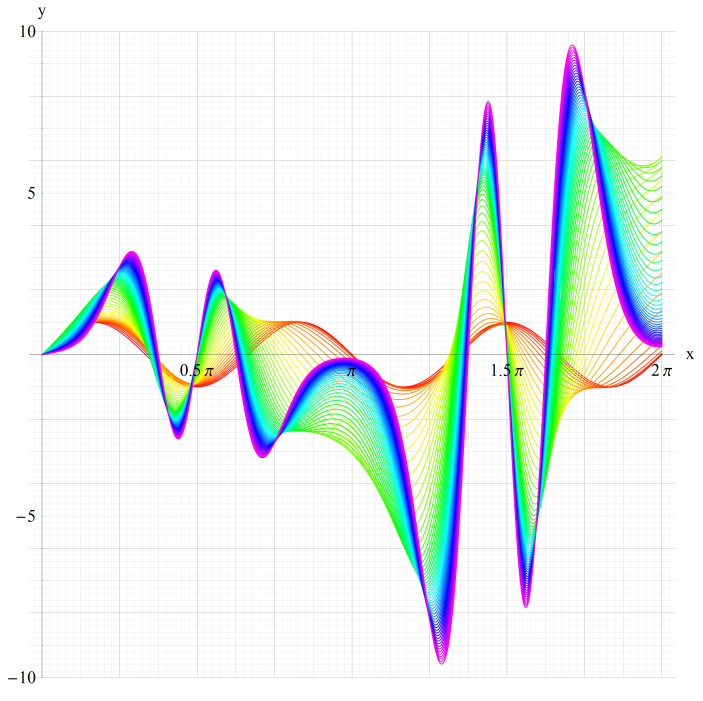
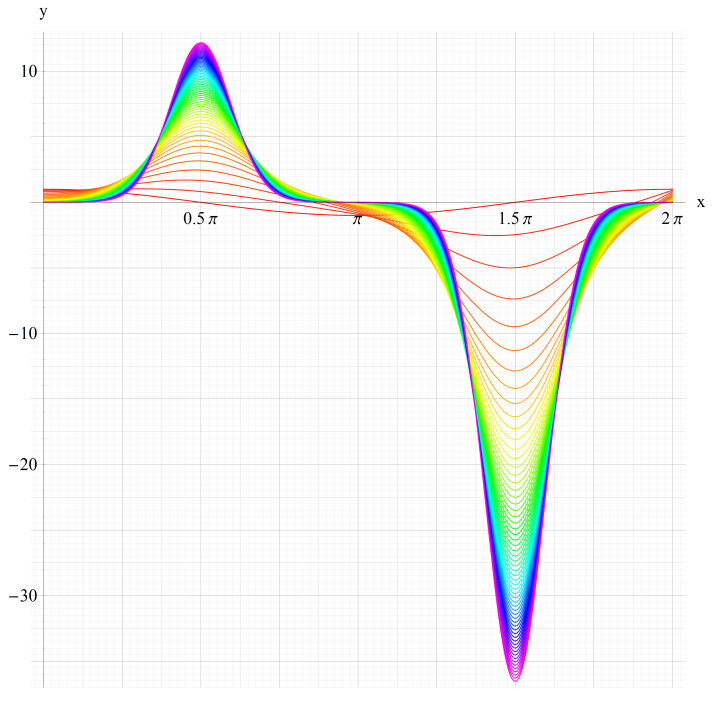
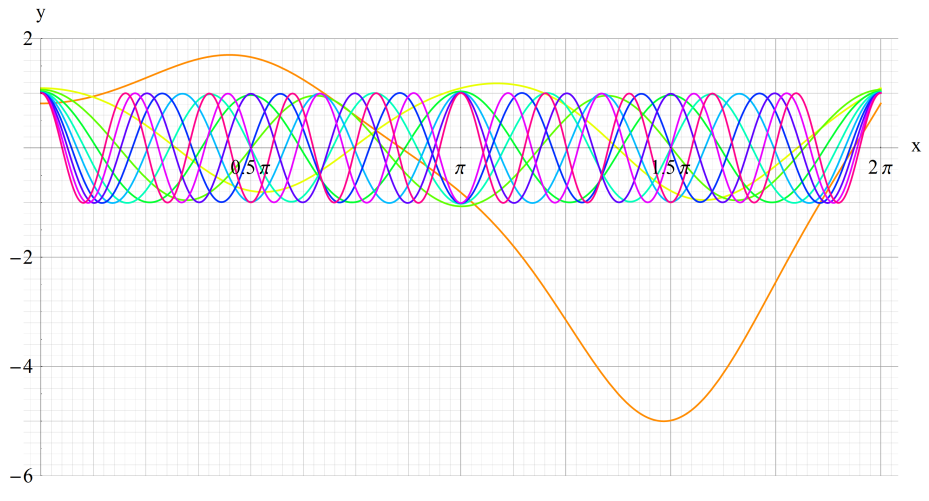
①ge1(q,x)、②ge2(q,x)
③ge3(q,x)、④ge4(q,x)
いずれも q=0~30 (+0.5)。
①gen(1,x)、②gen(5,x)、③gen(20,x)
いずれも n=0~10 (+1)。
さらに、第1種変形Mathieu関数は、Fourier 級数のほか、次のように 第1種 Bessel 関数を含む級数にも展開できる。 (以下、変数z1およびz2とする。)
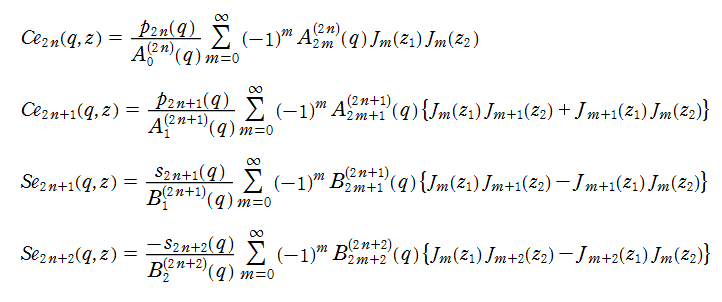
さらにこの展開式において、引数がz2の Bessel 関数Jを、第2種 Bessel 関数Yに変更した。
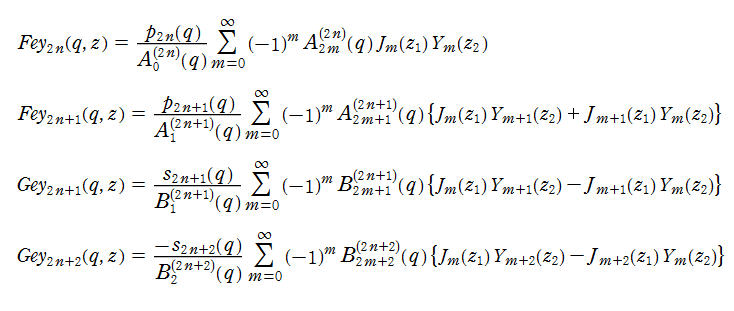
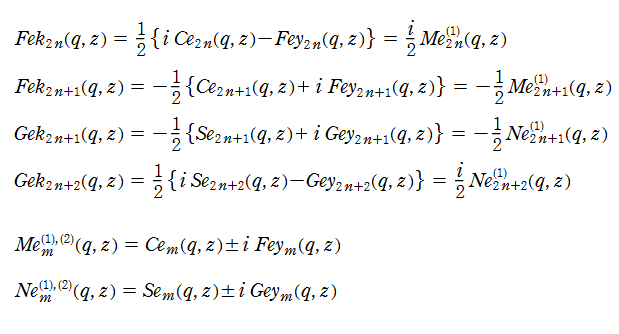
以上の第2種・第3種の解は、第2種Mathieu関数の記号等とは違って級数の収束が速く※2、また種々の積分表示式を満たすので、物理学等へ応用する際に都合が良い。
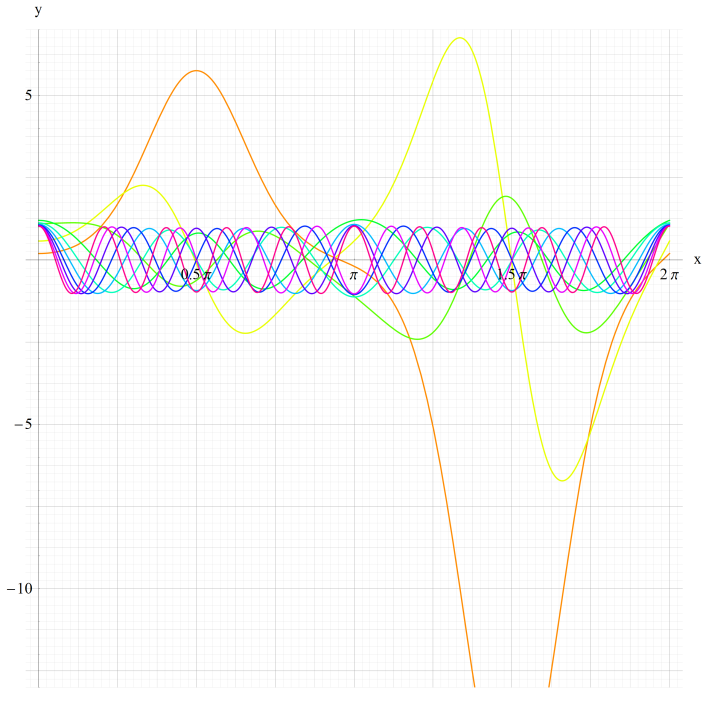
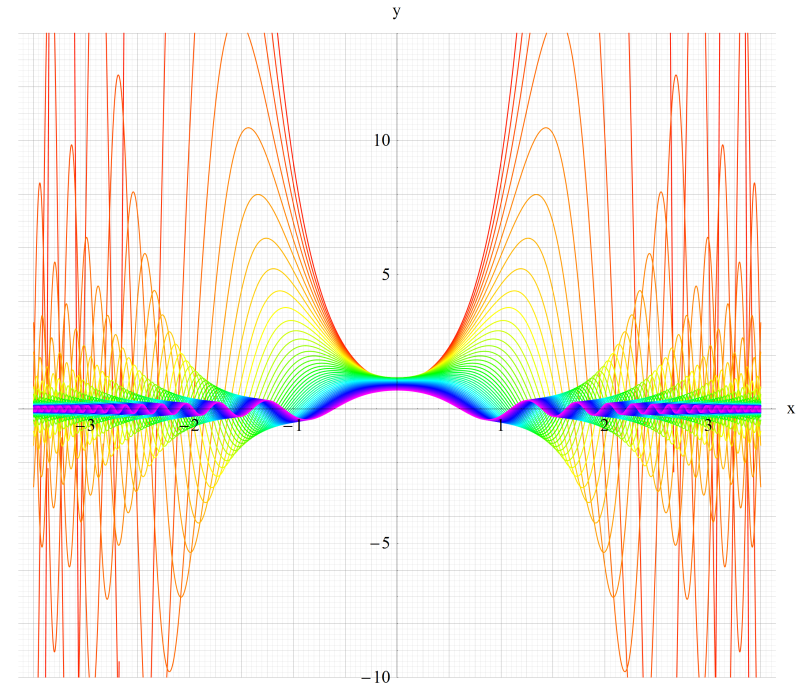
①Ce0(q,x)、②Ce1(q,x)
③Ce2(q,x)、④Ce3(q,x)
いずれも q=0.2~10 (+0.2)。
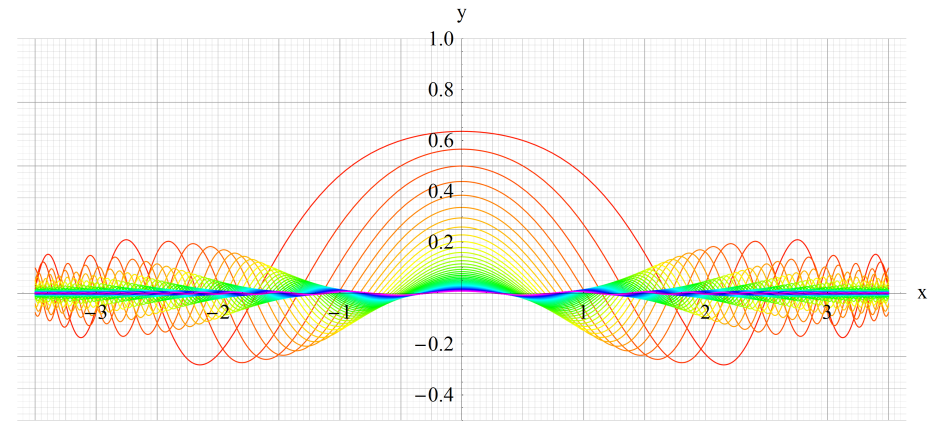
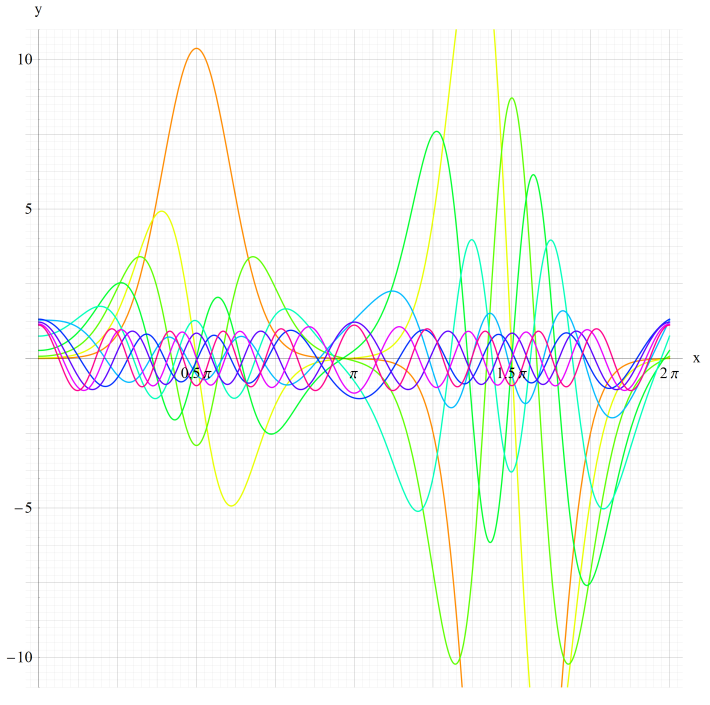
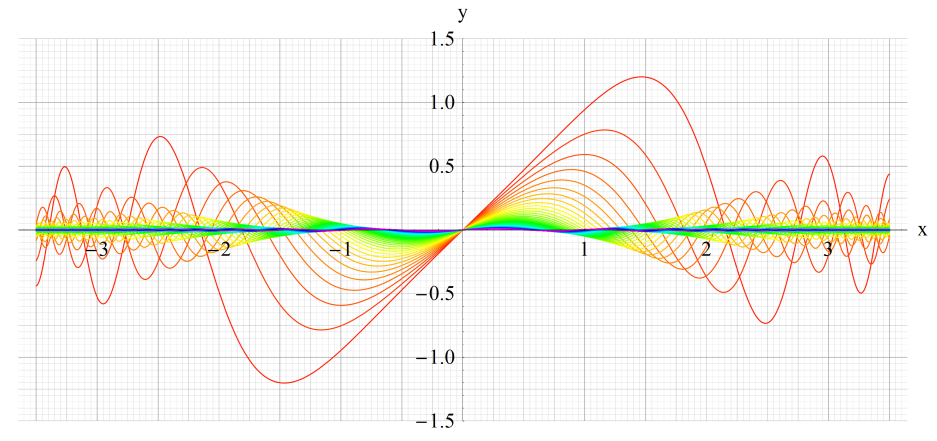
①Se1(q,x)、②Se2(q,x)
③Se3(q,x)、④Se4(q,x)
いずれも n=0~10 (+1)。
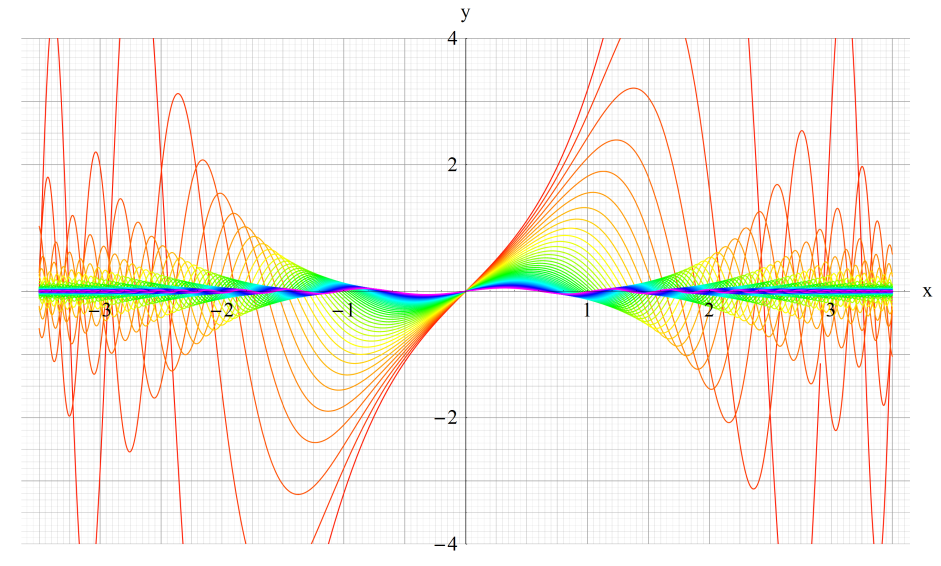
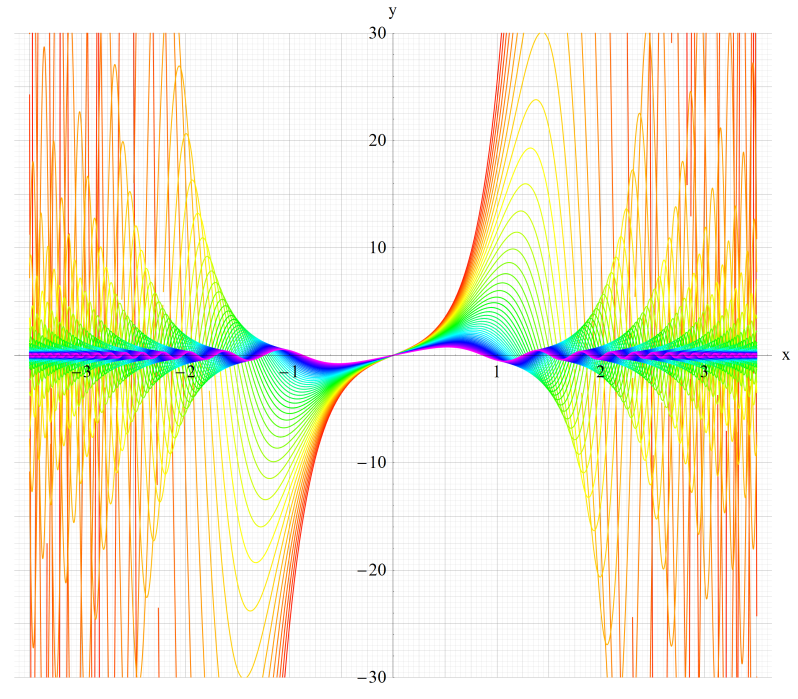
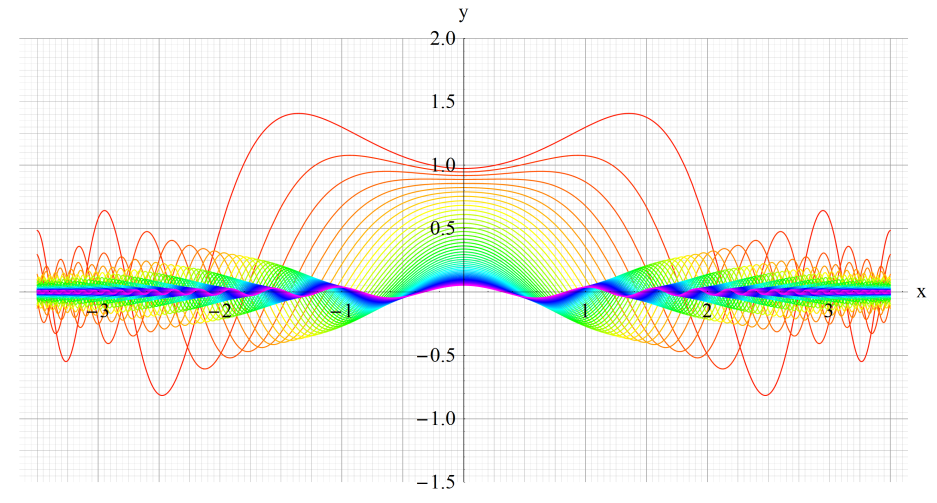
①Fey0(q,x)、②Fey1(q,x)
③Fey2(q,x)、④Fey3(q,x)
いずれも q=0.2~10 (+0.2)。
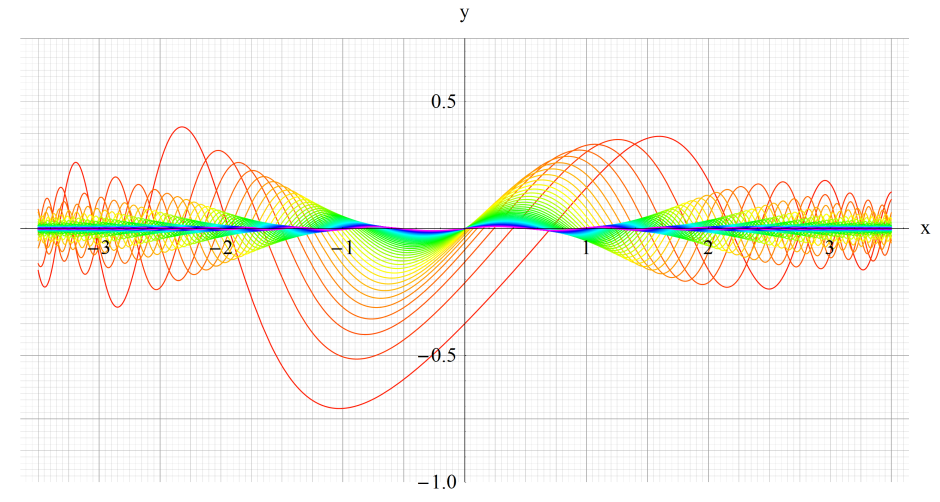
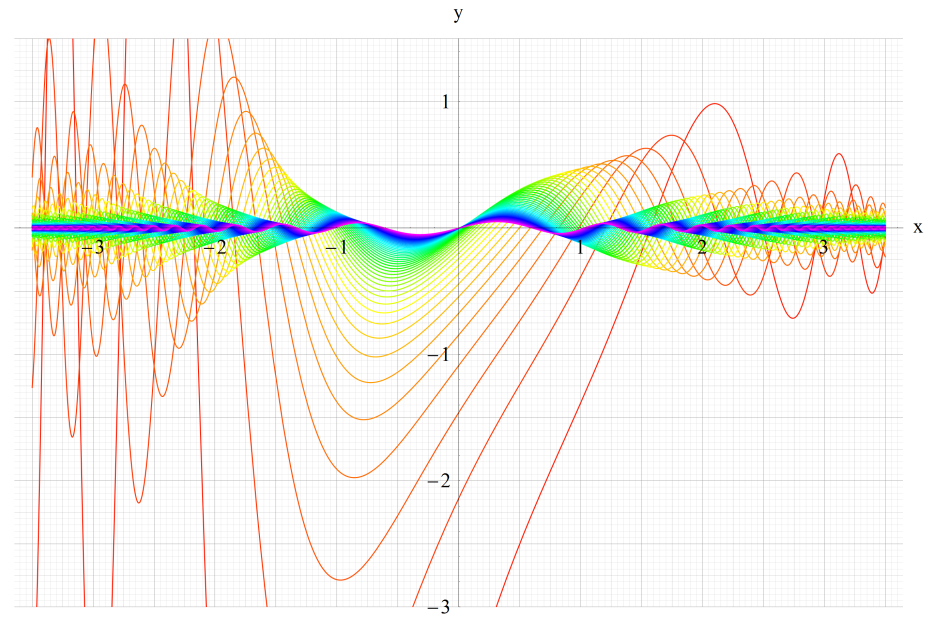
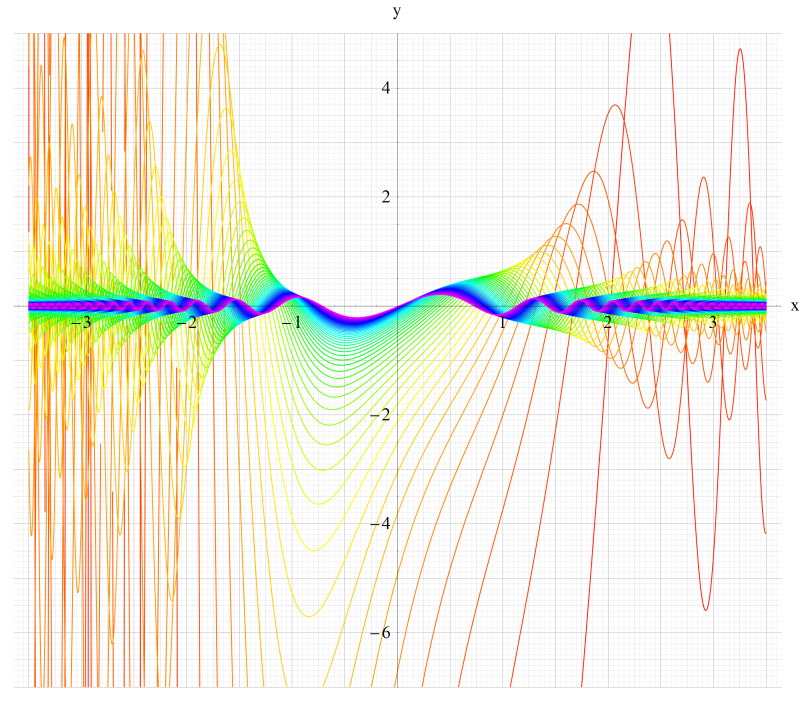
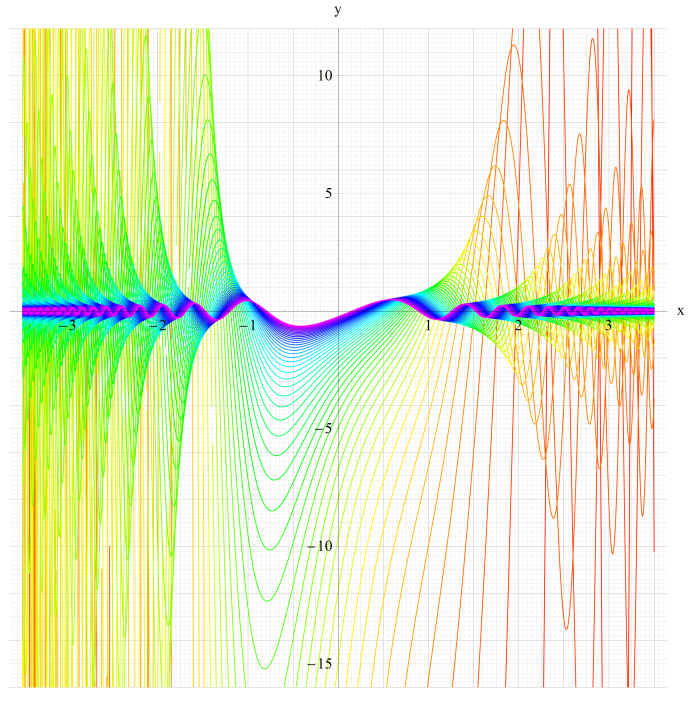
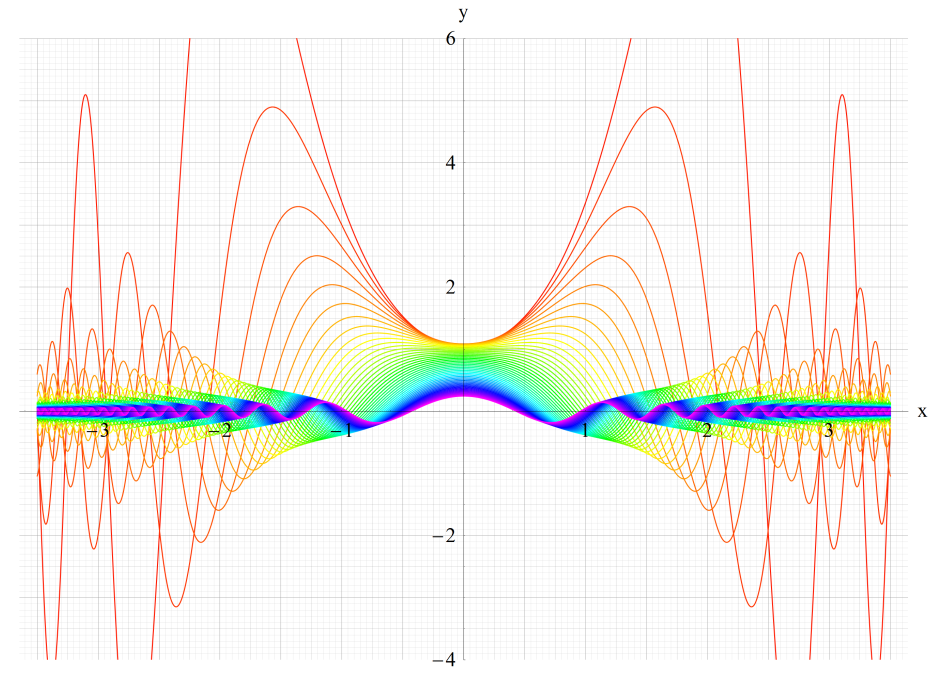
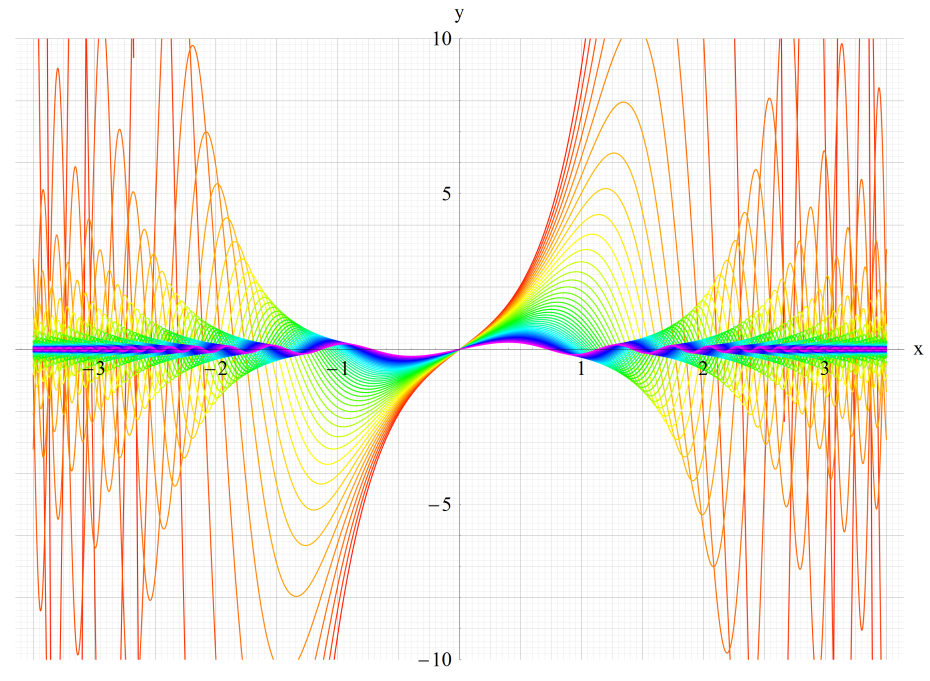
①Gey1(q,x)、②Gey2(q,x)
③Gey3(q,x)、④Gey4(q,x)
いずれも q=0.2~10 (+0.2)。
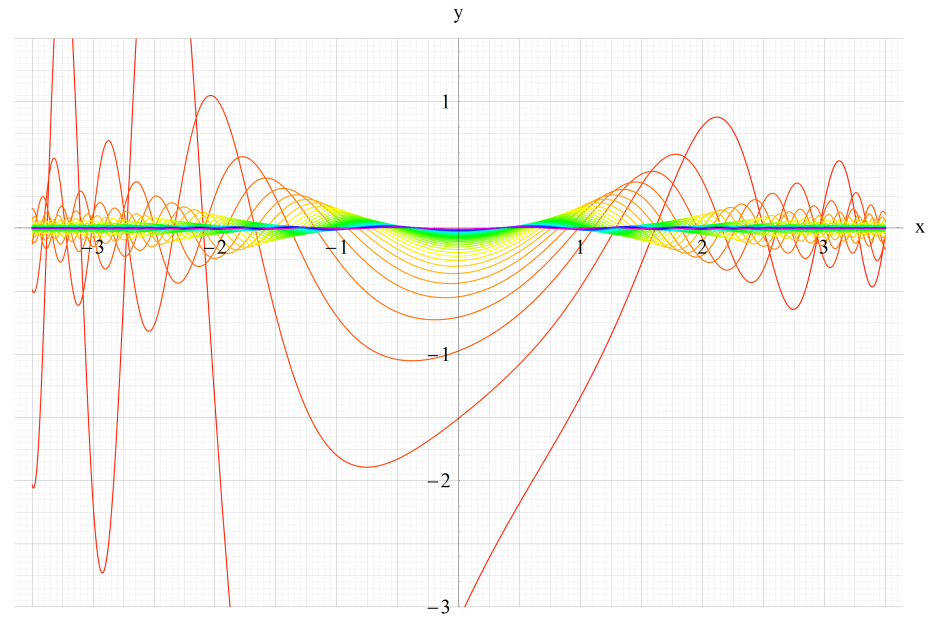
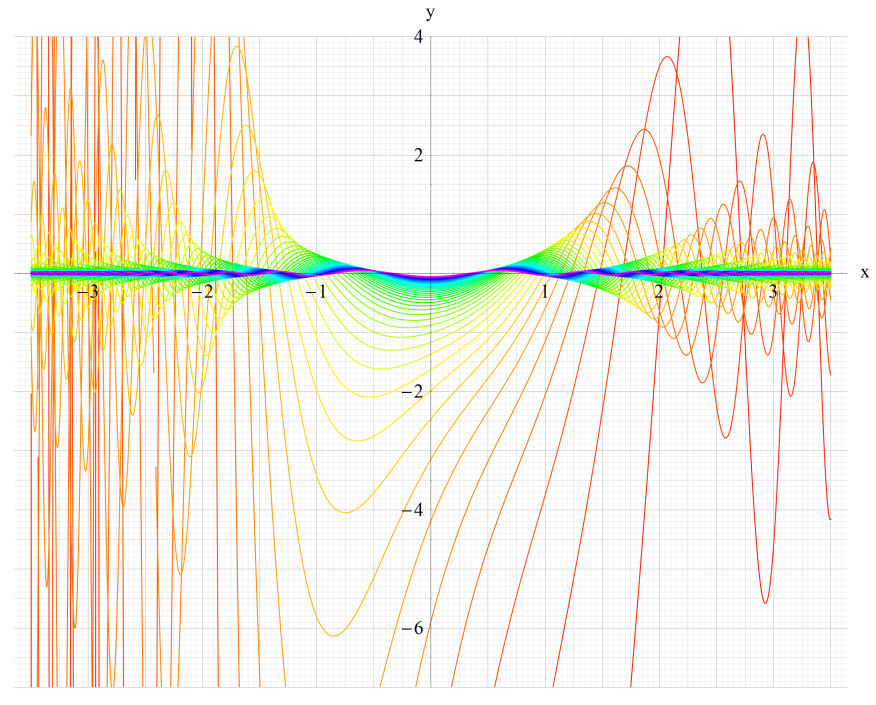
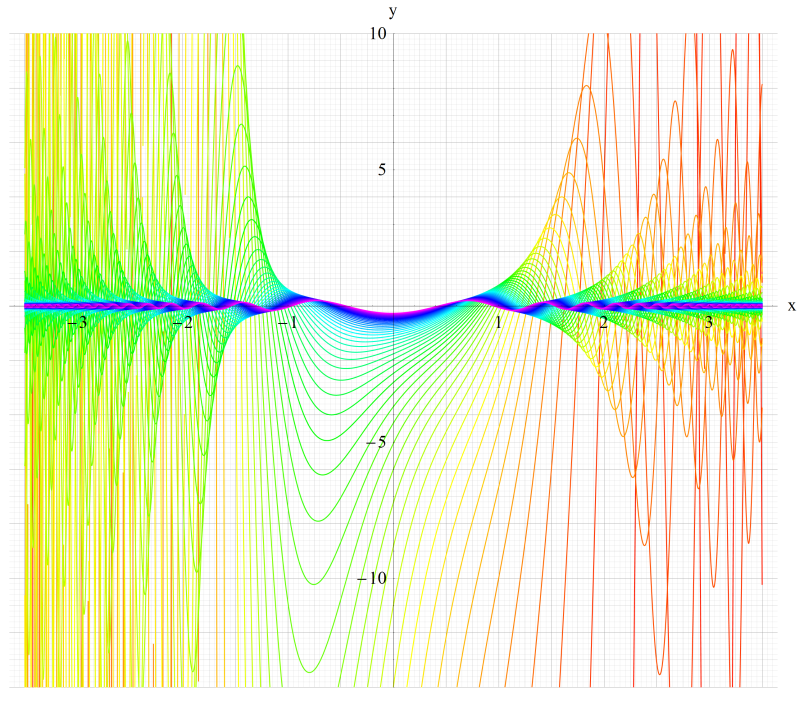
そして、解の様相は次の①~③に分類される。
① μが実数となるとき → 擬周期性基本解は一般に概周期関数になる。
② 特に①のうちμが有理数となるとき → 擬周期性基本解は周期関数になる。
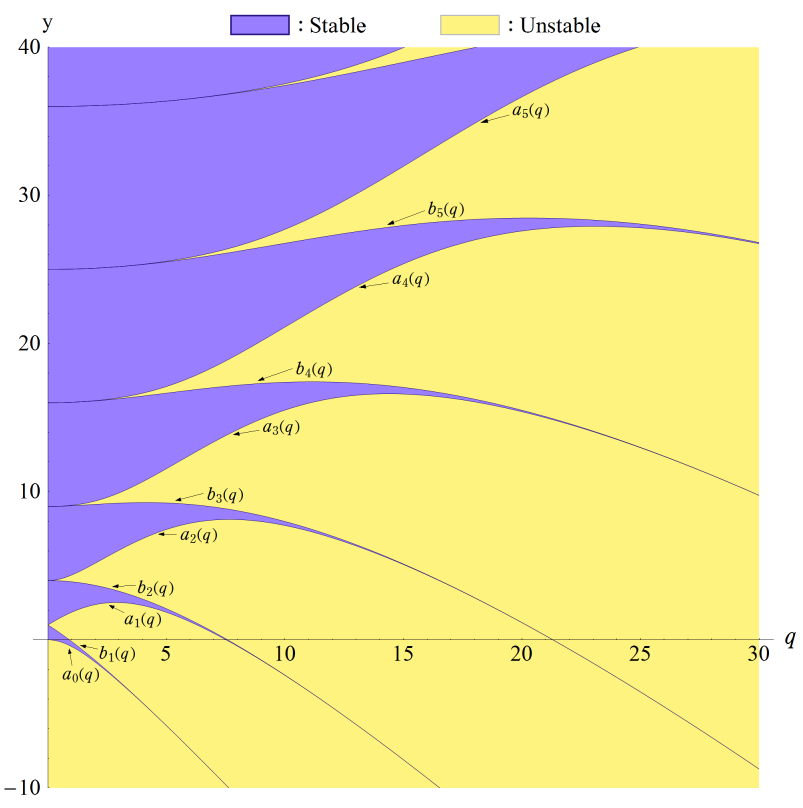
以上①,②の場合、擬周期性基本解の値は実定義域上で有界となる。このようなaの値域を「安定域」という。
一方、
③ μが①,②以外のとき → 二つの基本解の一方は擬周期関数になるが、いずれも有界な解ではない となるようなaの値域を「不安定域」という。
また固有値aは、qと次数vの関数と考えることができ、これを Mathieu 固有値関数という。 この時、周期偶関数cev(q,z)に対する固有値aはav(q)、 周期奇関数sev(q,z)に対する固有値aはbv(q)と表記される。
特に、vが非整数のときはav(q)=bv(q)となり、 vが奇数のときはav(q)=bv(-q)となる。 また、vが整数でq→+∞のとき、av(q)≒bv+1(q)となる。
②さらに広い領域。
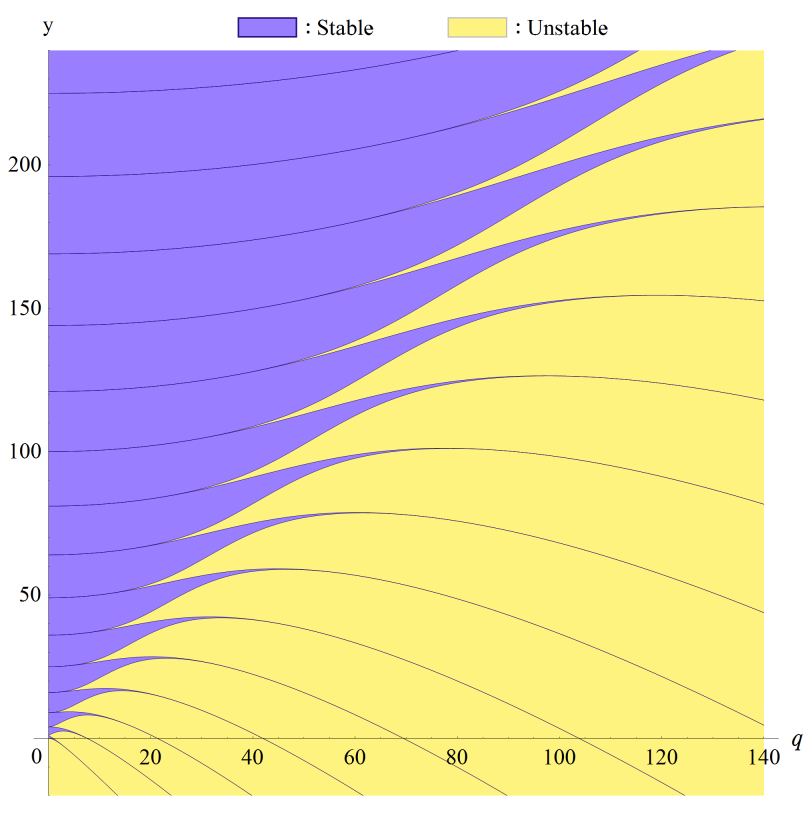
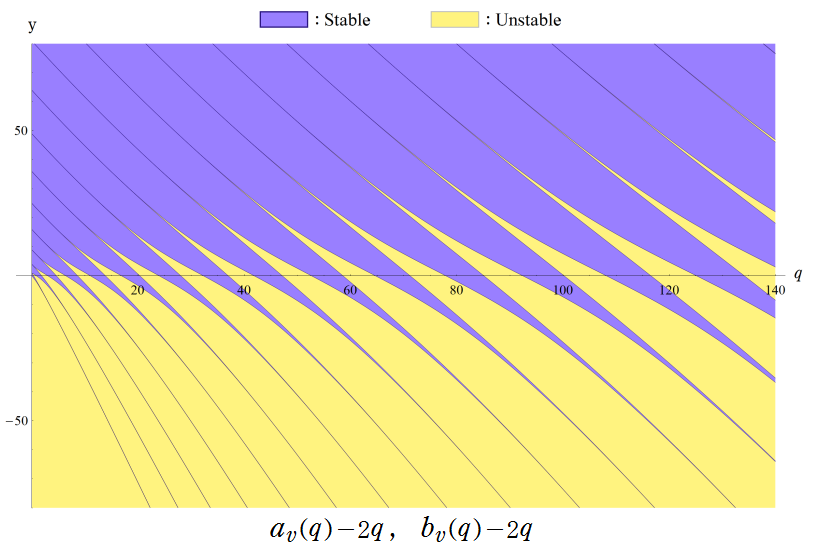
③ Mathieu 固有値関数から2qを引いた場合。
安定域・不安定域はy=2qの上下でほぼ半々になることが分かる。
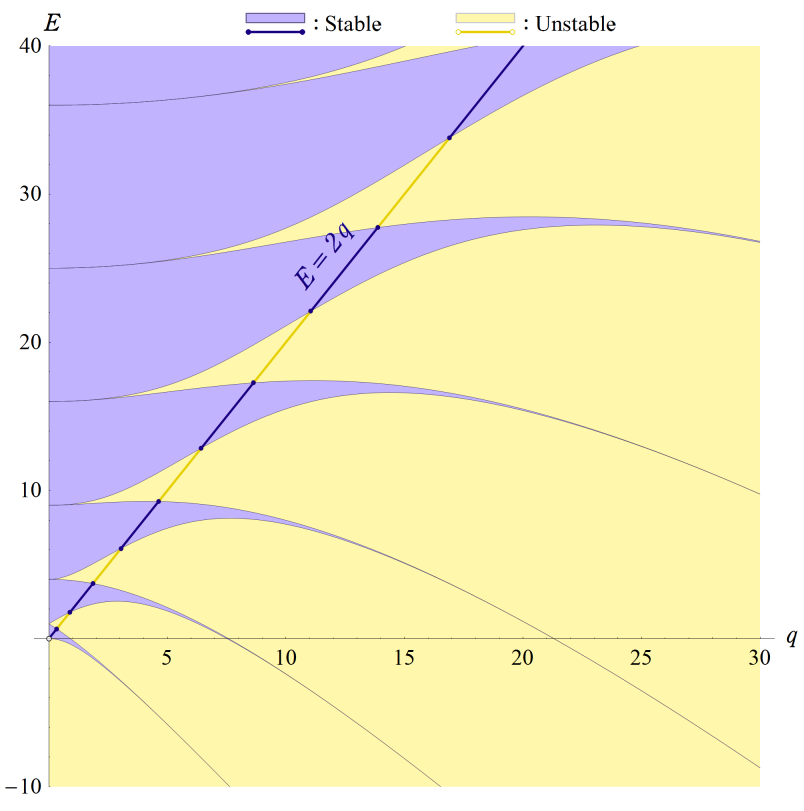
前述の電子が取りうるエネルギー範囲は、この図の原点を通る直線上(ただし、Planck 定数で決まる値より小さくはならない)で、 かつ、安定域と重なる無数の線分区間になる。
一方、各線分の間には不安定域を挟むギャップが存在し、そこでは波動関数は存在せず、エネルギーを考えることもできなくなる。
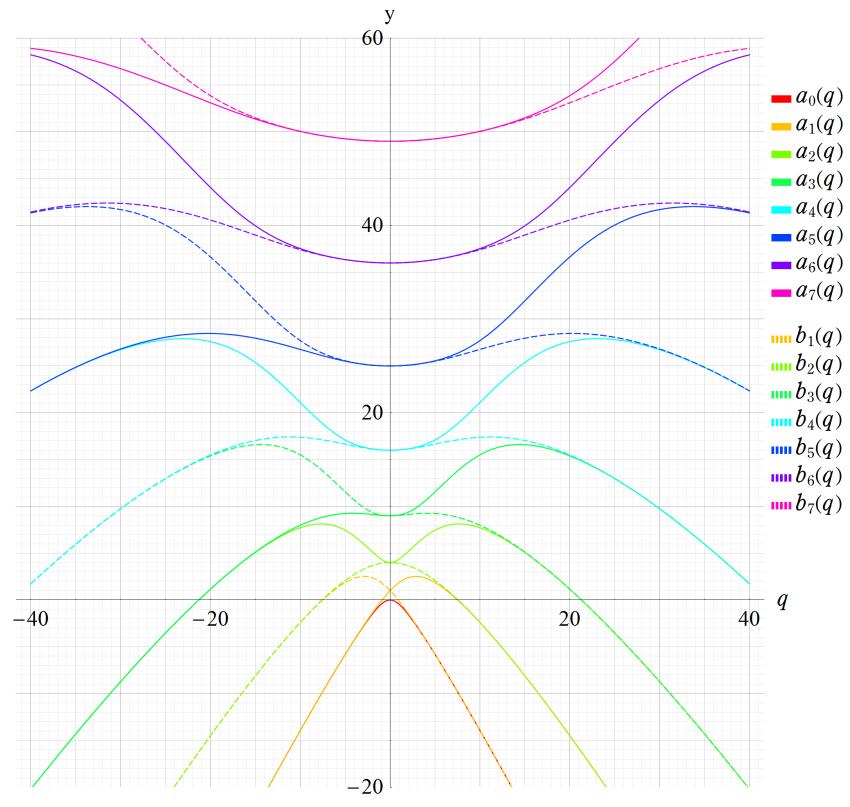
av(q):v=0~8 (+1)
bv(q):v=1~8 (+1)
bv(q):v=1~8 (+1)
vが非整数のとき、av(q)=bv(q)となる。
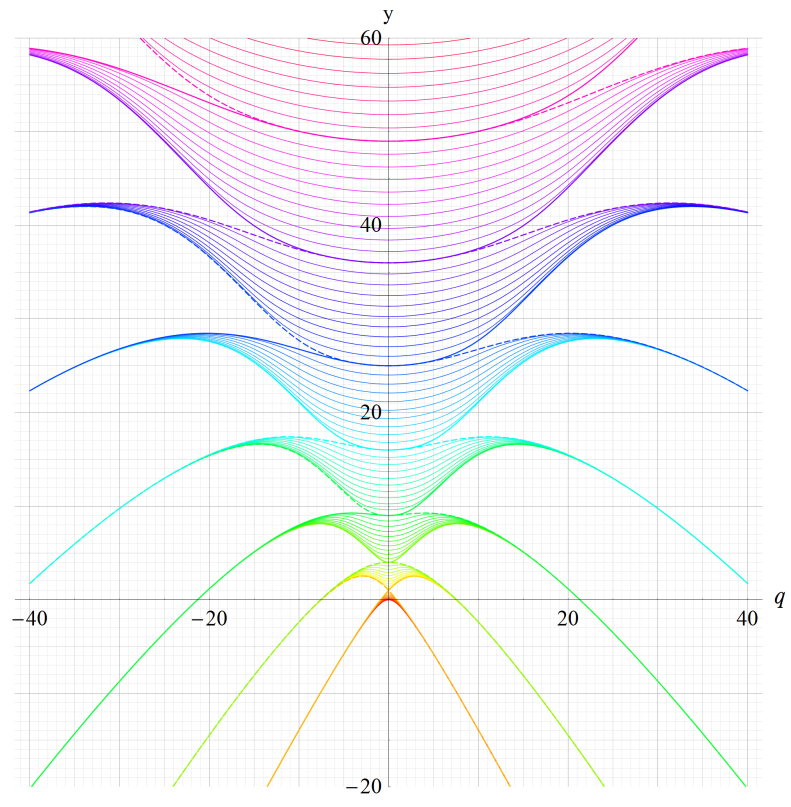
②原点の近傍を拡大した場合
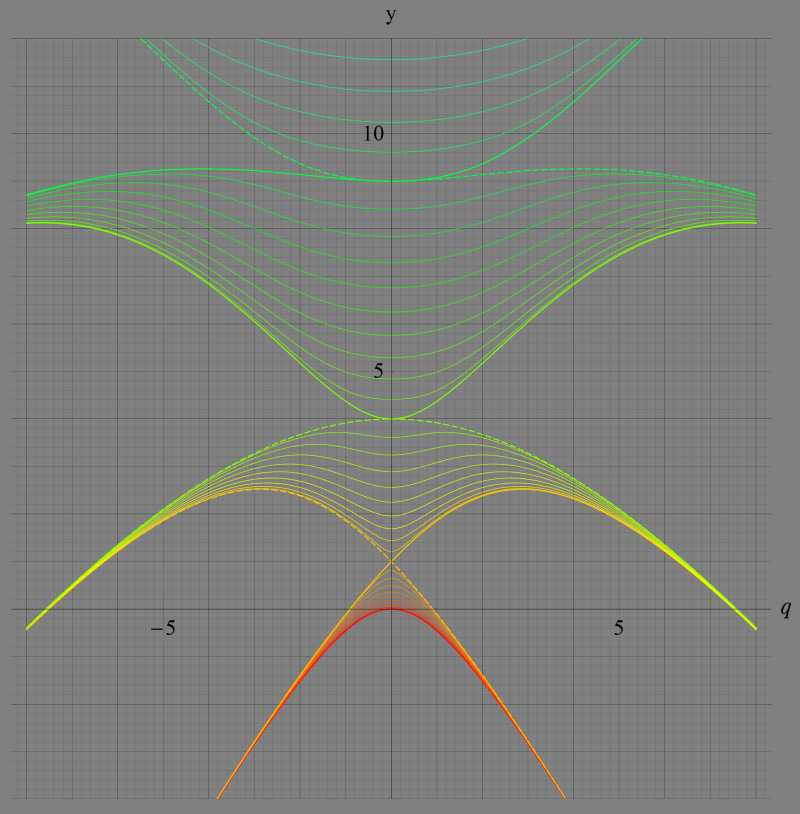
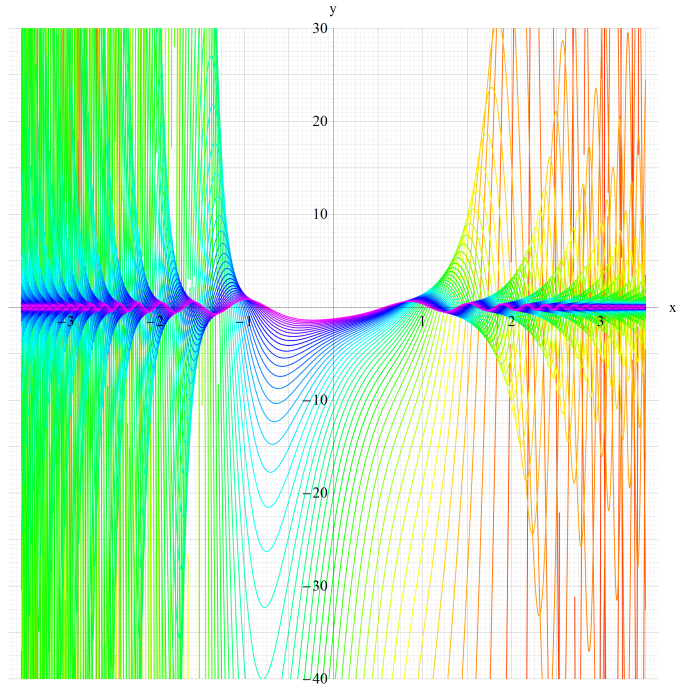
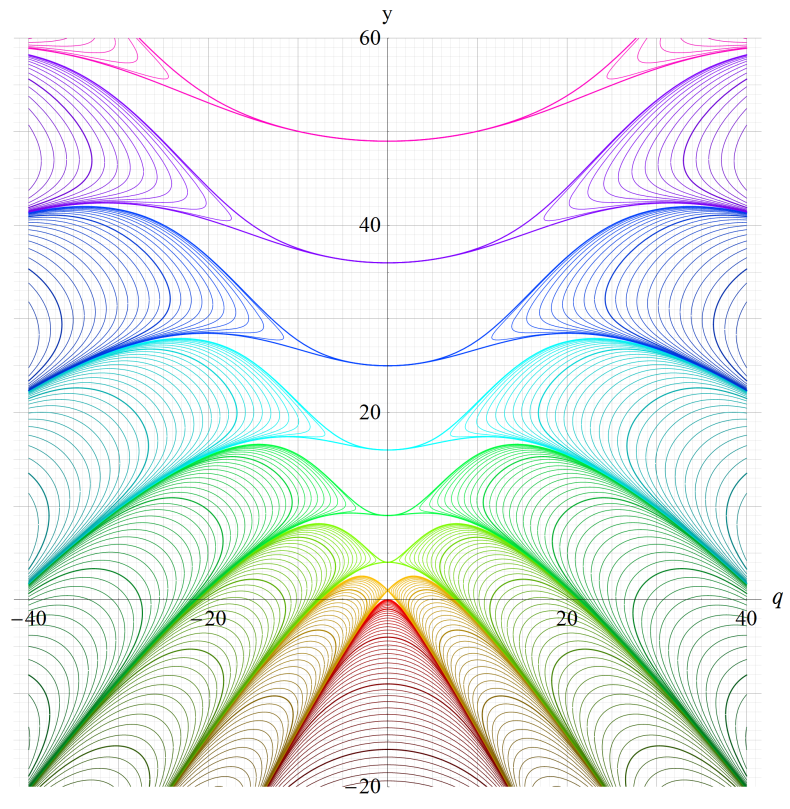
実変数の Mathieu 固有値関数au+vi(q)のグラフ。
u=0~8 (+1) かつ、v=0~5 (+0.1)。
色調がu/8、輝度が1-v/6で変化する場合。
vが整数のとき太線。
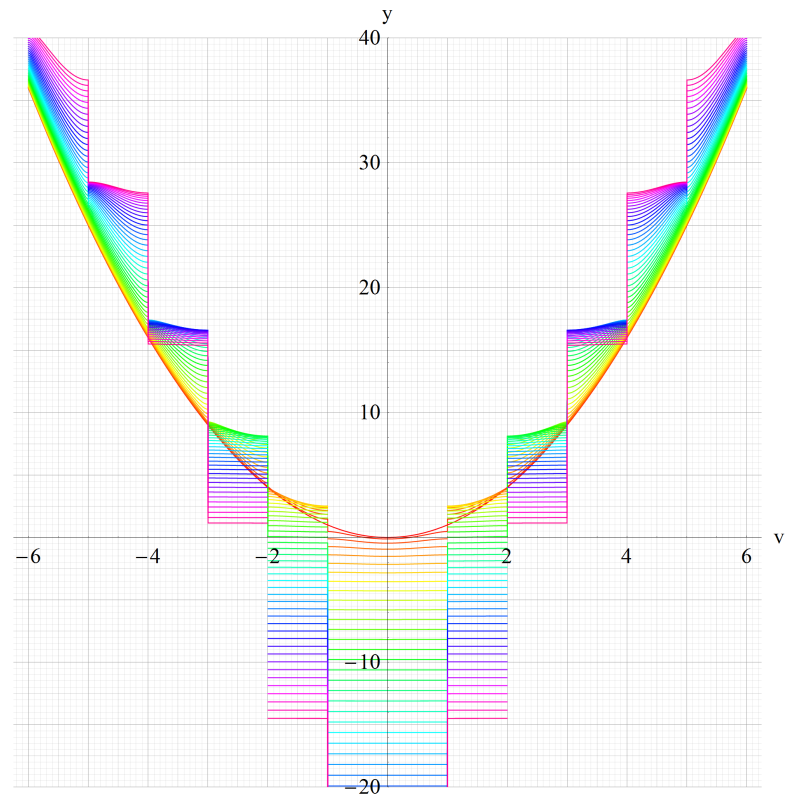
以上
(2019年7月31日)