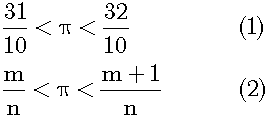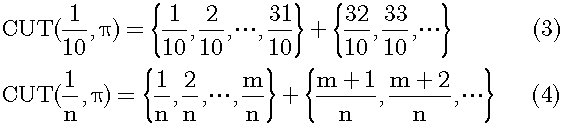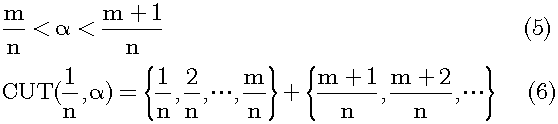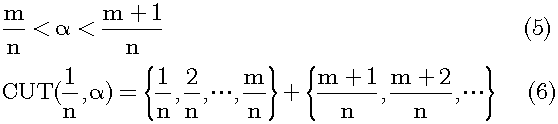デデキントの切断について
ユークリッド空間は脳内にしか存在しないので、数論とユークリッド幾何の結合でのべたように、幾何学を現実に適用するには、どうしても画素を基本とする考え方が必要です。そこで重要性を増すのはビットマップ画像です。画像の限界ビットマップで述べたように、コンピューターのビットマップ画像は単位正方形から構成されています。そのため曲線はギザギザになりますし、直角三角形の二辺をx軸y軸に平行にすれば、直角三角形の斜辺はギザギザになります。ところが十分に小さい単位正方形を用いれば、人間の眼には単位正方形は見えなくなります。例えば、デジタルカメラの写真は正方形の画素から構成されているはずですが、高解像度のデジタル写真は、人間の眼ではアナログの銀塩写真とは区別できません。
人間が眼球の網膜で光を検出した時点では画像は画素から構成されています。従ってユークリッド幾何の構成で述べたように、ユークリッド幾何はビットマップ画像から画素を隠して構成されます。網膜の段階ではビットマップ画像であって、ビットマップ画像は画素から構成されています。画素と画素の境界に幅0の線は存在しません。どう考えても、幅0の線や幅0長さ0の点は人間の神経系が創りだしたものです。ところが特に幅0の線は、現実に存在しているかのように見えます。図1に視力検査で用いられるランドルト環を示しました。ランドル環の黒いリングの切れ目の部分に注目します。白い切れ目と黒いリングの上下の境界線は、赤で強調してありますが、幅0の線のように見えます。しかし、それは我々の神経系が創作したものであって、我々の眼は本当は幅0の線では無く、切れ目の白い画素を認識しているのです。それは視力検査によって明らかになります。徐々に小さなランドルト環を見せられるに従って、切れ目の白い画素を認識していると意識するようになります。さらに小さなランドルト環を見せられて、切れ目の白い画素が認識できなくなると、ランドルト環は完全に黒いリングに見えます。
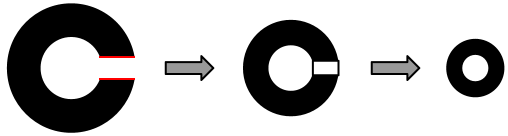
図1.ランドルト環
このように幅の無い線は我々の神経系の創作物です。ここでユークリッドの定義する幅0の線と、ビットマップ画像における直線の関係につて考察します。図2に幅0の直線と画素の関係を示します。ユークリッド幾何の構成で述べたように、三次元物体のエッジはビットマップ画像の画素と画素との境界線に対応します。図2の上段に白い画素と黒い画素の境界線として幅0の線分を赤で示しました。脳で画素が隠されるので、我々の目には連続的な空間における幅0の線のように見えます。それを図2の中段に赤い線で示しました。しかし、ランドルト環に関する考察で述べたように、幅0の線は白い画素と黒い画素の両方が認識されないと見えません。そうであれば、黒い画素の直線で代用する方が効率的です。これを図2の下段に示しました。
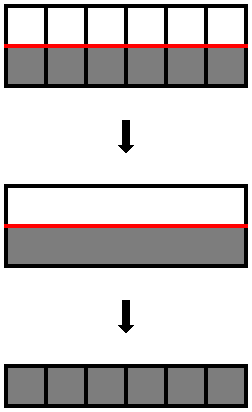
図2.線の変換
実際にユークリッド幾何を学習する場合、幅0の直線を鉛筆で書いた幅のある直線で代用します。勿論、鉛筆で書いた直線は画素から構成されます。芯の太さがあり、使う鉛筆によって画素の大きさは決定されます。さらに人間の目の分解能は約0.1mmですので、それより小さな画素は用いることが出来ません。それでも、普通の人は何の問題も感じません。おかげで紙と鉛筆のユークリッド幾何が成立するのです。これは厳密には間違っていますが、誰も間違いとは認識しません。人間の認識の仕方が、小さな誤差は無視するようになっていると思われます。
これが線画の原理となっています。西洋画におけるデッサンは、三次元物体の輪郭を線で描く事が基本となります。東洋の絵画でも同様であり、現代の漫画も、原始時代のアルタミラやラスコーの洞窟壁画も同じです。これは人間の三次元物体の形の基本的認識方法の一つと思われます。ユークリッドは「線とは幅のない長さである」と定義しています。それを人間は長さも幅もある線に変換しているのです。このように通常の画像は自然数1に対応する画素から構成されているのです。人間の描いた画像は全て有限の画素から構成されています。また人間は有限の画素しか認識できません。このように我々の認識する現実は、有限の自然数から構成されているのです。
2. 自然数の有限性
ここまでに述べたことで明らかなように、生命の認識はあくまでも自然数1を基本とします。そこで自然数1を基に数学を構築することを考えます。自然数1から一般の自然数を構成する方法がそのまま自然数の定義になります。自然数の定義として、ペアノ自身によって記述されたペアノの公理を記載します。
- 1 は自然数である
- 任意の自然数 a に対して、a+ が自然数を与えるような右作用演算 + が存在する
- もし a, b を自然数とすると、 a+ = b+ ならば a = b である
- a+ = 1 を満たすような自然数 a は存在しない
- 集合s が二条件「(i) 1 は s に含まれる, (ii) 自然数 a が s に含まれるならば a+ も s に含まれる」を満たすならば、あらゆる自然数は s に含まれる。
これは広く認められた自然数の定義です。自然数を定義しようとすれば、どうしてもペアノの定義と似たものになります。そして、五番目の数学的帰納法 については、普通の数学では認めるしかありません。そうすると必然的に無限大の自然数は存在しないことになります。以下に数学的帰納法による証明を記載します。
- 1は有限である。
- もしも任意の自然数kが有限であれば、自然数k+1は有限である。
- 任意の自然数nは有限である。
つまり、どんな自然数でも有限であるとなります。こうして有限の自然数のみを対象とする数学が構築されます。この段階の数学はコンピューターの扱える範囲の数学となります。本質的にコンピューターは、自然数または自然数の比しか扱えません。どんな有理数でも扱えますが、実用的には有限の桁数の小数を用います。ある意味では、この段階で数学は十分であるとも考えられます。ギリシャ以外の数学はこのような数学であったと思われます。例えばバビロニアの数学では、既にピタゴラスの定理は知られていたと思われます。ところが2の平方根などは、近似値を計算して事足れりとしていたようです。メソポタミア人には無理数が分数で表せるかどうかには興味がなく、実用に役に立つかどうかが重要であったようです。実用を考えた場合、必要な精度まで近似値が計算できれば十分で、ある数が無理数であるか有理数であるかは重要ではありません。
自然数によって実数を定義するために、まず最初にユークリッドによる数の定義を見てみます。
第7巻 定義
- 単位とは存在するものおのおのそれぞれがそれによって1とよばれるものである。
- 数とは単位からなる多である。
この定義について説明します。このようにユークリッドは数を自然数に限定します。これは現代になってみると卓見と言えます。自然数による世界の認識で述べたように、本質的にコンピューターは自然数しか扱えないので、実用数学では自然数または簡単に自然数に変換できる小数を扱います。この事実はコンピューターの出現によって明確になっただけで、昔からそうだったのです。普通の人にとっては円周率は3.14で問題有りません。これは中学校までの数学では十分すぎるぐらいです。例えば、直径10cmの円の円周は314mmとなりますが、製図に慣れない人が描いた場合、すぐに1mmや2mmの誤差を生じます。上手な人でも、芯を十分に削ってもHBの鉛筆の線の幅が約0.5mm程度なので、これ以上の精度は必要無いのです。人間が鉛筆で線を描く場合、芯の大きさの画素を並べて線を構成していることになります。より精度を求めるなら、製図用のペンを用いることになりますが、線幅0.1mm程度が限界です。だからコンピューターの出現以前は、精度が低かっただけで、実質的にはビットマップ画像を用いていたのです。
コンピューター時代になると、紙と鉛筆の幾何学より遙かに精度が上がります。具体的には、一般に用いられている倍精度の浮動小数点数で、10進法で15桁程度の有効数字となります。ただし、この精度は現代ではパソコンで簡単に得られるレベルなので、より高精度な計算が必要なら、もっと精度を上げることは出来ます。例えば人工衛星の軌道計算でも、円周率の値は小数点以下30桁程度の近似値を使用しています。これらの数は簡単に自然数に変換できます。例えば小数点以下30桁の小数であれば、1030倍すれば自然数に変換されます。このように現実に使用可能なのはユークリッドの定義した数、すなわち自然数だけなのです。現代ではコンピューターがありますから、あらゆる有理数は簡単に自然数に変換できます。
このように現代ではユークリッドの数の定義の意義は増していると考えられますので、この定義を用いて実数を定義します。ここで通常の数と区別するために、ユークリッドの定義する数を「数」と表します。まず最初に図3に、0.1刻みで目盛りをつけたユークリッド平面における数直線と画素を重ねて示しました。この数直線は負の数を含まず、原点から正の方向に伸びる数直線です。画素は灰色の一辺の長さが0.1の単位正方形で示しています。赤でユークリッド平面における数直線を示します。ここにはπの近くだけをピックアップしてあります。0.1は単位正方形の一辺の長さを表しますが、単位正方形は自然数1としての性質を持っています。自然数による世界の認識で述べたように、自然数1はプラトンの三原則を満たします。そうすると単位正方形の一辺である0.1は、必然的にユークリッドの単位の定義を満たします。
ユークリッド平面における線分の長さは無理数の場合もあり、無理数は有理数では表せません。つまり無理数はユークリッドの定義する数に変換出来無いのです。そのためユークリッドは、ユークリッド平面における線分の長さを量と呼んで数と区別しています。無理数の長さの線分はユークリッド平面上にしか存在しませんから、必ずユークリッドの定義する数で近似しなくてはならないのです。
このように現代ではユークリッドの数の定義の意義は増していると考えられますので、この定義を用いて実数を定義します。ここで通常の数と区別するために、ユークリッドの定義する数を「数」と表します。まず最初に図3に、0.1刻みで目盛りをつけたユークリッド平面における数直線と画素を重ねて示しました。この数直線は負の数を含まず、原点から正の方向に伸びる数直線です。画素は灰色の一辺の長さが0.1の単位正方形で示しています。赤でユークリッド平面における数直線を示します。ここにはπの近くだけをピックアップしてあります。0.1は単位正方形の一辺の長さを表しますが、単位正方形は自然数1としての性質を持っています。自然数による世界の認識で述べたように、自然数1はプラトンの三原則を満たします。そうすると単位正方形の一辺である0.1は、必然的にユークリッドの単位の定義を満たします。
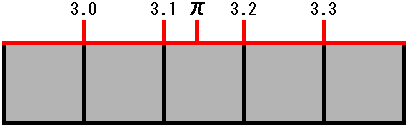
図3.数直線
そう考えると、単位というのは動かしがたいもの、何となく高尚なものと思うかも知れませんが、それは違います。ユークリッド平面をデジタル化する時に単位は必要になりますが、デジタル化はあくまでも実用性が目的です。自分が便利なように単位を決めて良いのです。この場合の単位というのは、ビットマップ画像の画素に相当しますが、画素の大きさは目的に応じて比較的自由に選択できます。画像を道端の看板として使うのか、証明写真なのか、あるいは精密機械の設計図なのか。必要な精度に応じて単位の大きさは選択可能です。
こうして決められた単位は二重の意味を持つことになります。一つは分割不能な自然数1であり、もう一つはユークリッド平面上の線分の長さです。上の例では0.1は二重の意味を持っています。それを利用してπを近似することが可能です。この例では赤い目盛りを用いて、ユークリッド平面上の線の長さを比較することによって、πを3.1と3.2の間に挟むことが出来ます。
ここでユークリッドの「数」を有理数にまで拡張します。この例における小数は分母10の分数ですから、単位1/10の「数」と見なすことが可能です。次に一般の有理数について考察します。それには単位の大きさを1/nとします。その上で単位1/nの「数」を大きさの順に並べれば、隣接する二つの「数」でπを挟むことが出来ます。以下の式(1)は単位1/10の「数」の例、式(2)は単位1/nの「数」の場合を表します。なお、式(2)のm,nは自然数を表します。
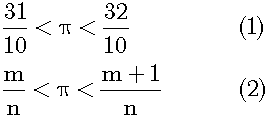
以下の式(3)のCUT(1/10,π)は単位が1/10の「数」のπによる分割を示しました。単位が1/10の「数」はπより大きい「数」の集合とπより小さい「数」の集合に分けられます。式(4)のCUT(1/n,π)は単位が1/nの「数」のπによる分割を示します。「数」は単位からなる線分の長さを表します。例えば「数」31/10は単位1/10の31倍の長さの線分となります。1/nもm/nもそれぞれ線分の長さを表しています。またπそのものは長さπの線分を表しており、点πで数直線を切断して生じる線分を表します 。
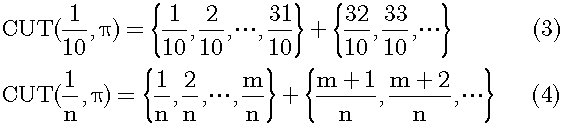
一般の無理数αもπと同様です。単位を1/nとした場合の「数」の無理数αによる切断は、式(2),(4)のπをαに入れ替えることによって、式(5),(6)に示されます。1/n<αであれば、アルキメデスの公理により、必ず単位1/nの「数」でαを挟むことが出来ます。ここでnを無制限に増加させると、任意の有理数をαより大きいものと小さいものに分けることが出来ます。これはデデキントの切断と等価です。
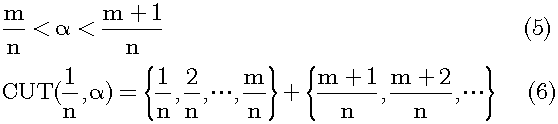
ここで任意の無理数αと、αより大きい任意の無理数βを考え、両者の差をεとします。これを式(7)に示します。アルキメデスの公理により、1<nεとなる自然数nが存在します。この不等式の両辺をnで割ると式(8)となります。ここでnを十分大きくとると、式(9)(10)に示したようにαとβを別々の「数」で挟むことが出来ます。ここで、j,k,nは自然数を表します。
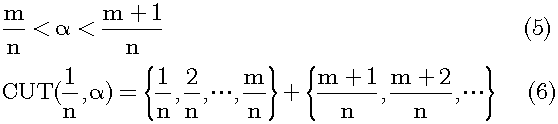
このように任意の異なる二つの無理数は必ず別の「数」のペアで挟むことが出来ます。しかも単位である1/nはnを増加させることによって、いくらでも小さく出来ます。このように「数」によって無理数を任意の精度で近似することが出来ます。逆に無理数を、任意の単位1/nについて「数」を切断するものと定義することも出来ます。この定義はデデキントの切断と等価です。さらにデデキントは「連続性と無理数」(Continuity and Irrational Numbers)で異なる二つの切断の間には、必ず二つ以上の有理数が存在すると述べています。つまり無理数と無理数の間には、必ず二つ以上の有理数が存在するのです。これは無理数の総数は有理数の総数を超えないことを意味します。そして有理数は自然数のペアと考えられるので、世界は自然数で記述可能ということになります。さらに自然数は常に有限ですので、いくらでも大きい自然数は有り得ますが、どんな自然数も有限です。