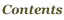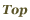PyQtでお手軽GUI開発♪―――は可能だったか？ 第12回　モザイクを外せ！編

PyQtでお手軽GUI開発♪―――は可能だったか？ 第12回　モザイクを外せ！編

　前回、doubleの精度限界にぶち当たって画像がモザイクになってしまいました。このモザイクを外すためには倍精度浮動小数点よりも更に精密な計算が必要になるわけです。そういうことをやろうとすると、普通ならば特殊な外部ライブラリを使ったりしなければなりませんが、Pythonの場合は素の状態でそれを乗り越えられる可能性がありました。それが固定小数点演算です。


固定小数点演算

　コンピュータで小数を扱う場合のデータ形式に浮動小数点形式と固定小数点形式というのがあります。


　固定小数点とは例えば 123.45 といった小数があれば、12345という整数があって、その下から2桁目に小数点が打たれていると考えて計算する方式です。

　浮動小数点形式とはこれを 1.2345×102というように値の部分（仮数部）とそのスケールを示す値（指数部）を別々に保存して計算する方式です。


　一般的にコンピュータで小数を扱う場合、特に現在ではまずほとんどの局面で浮動小数点が使われます。なぜなら固定小数点を使うメリットがほとんどないからです。


　理由はいくつかあって、まず固定小数点では浮動小数点に比べて表せる値の範囲が圧倒的に狭くなってしまうことです。

　現在主流の64ビットのdoubleでは有効桁数が15～16桁で、10-308から10308の範囲の値が表現できます。

　それに対して64ビットの固定小数点だと、これは結局64ビット整数の表せる範囲になるので、約19桁程度の範囲しか表せません。


　また固定小数点の場合、値のスケールによって計算精度が変わってしまうことも問題です。

　例えば小数点以下桁数が3の固定小数点を扱っている場合、計算している値が1～10のスケールなら精度4桁しかありませんが、値が100～1000なら精度6桁で計算できます。1,000,000,000,000くらいの値なら16桁ぐらいの精度で計算できることになります。


　しかしこれはかなり困った性質で、例えば大きな数と小さな数の乗除算が出たような場合、値がどのくらいのスケールになるかに常に注意していないと、結果の信頼性が保てません。これが浮動小数点ならオーバーフローなどがなければ有効桁は保証できているわけですが―――むしろ固定小数点のこのような弱点を克服するために浮動小数点ができたようなものでしょう。


　というわけで固定小数点演算が使われる局面は多分大きく二つ、ショボいCPU上で実数計算を高速に行いたい場合と、もう一つは勘定系（ただしこちらは10進の固定小数点）でしょうか。


　パソコンのCPUはペンティアム以降は基本的にFPUがついていて、浮動小数点演算を高速に行えるようになっていますが、それ以前の場合にはソフトウェアで処理されていたため、浮動小数点演算は非常に低速でした。そこで高速性が必要な局面ではほぼ整数演算と同等のスピードで行える固定小数点演算が代りに使われました。今でも組み込み系などではそういうことも行われているようです。


　それともう一つお金の計算に使われるデータに10進固定小数点型というのが使われる場合があります。

　金勘定の場合は小数点以下は常に数桁あればよく、その代わりに誤差は絶対許されません。

　なぜならお金の場合は10-35円昇給したよとか言われても全然嬉しくないわけで、利息計算とかに“銭”単位が出ることはありますが、それなら小数点以下4桁くらいあれば十分です。

　またよく知られているように 1/5 という数は10進法では 0.2 ときれいに割り切れますが、2進法では無限小数になってしまいます。こういった挙動の差があると勘定系の場合では非常に困ります。そこで10000を0と見立てた10進固定小数点演算をするわけです。


　ともかくそういうわけで固定小数点演算をしたければ自前で計算ルーチンを作る必要が出てくるわけです。


固定小数点計算の原理

　とはいっても基本は小学校で習った小数の計算です。


　まず小数の加減算を行う場合ですが、加減する数の小数点以下桁数が等しければ、小数点を無視して整数とみなして加減した結果に、あとから元の位置に小数点をつけてやればOKです。

　加減する数の桁数が異なっている場合は、以下のように小数点の位置を揃えて同様に計算します。


　例えば　1.234 + 56.7 = 57.934　という場合は下の左のように計算しますが、これは右のように計算してあとから3桁目に小数点をつけてやっても同じことです。

    1.234                   1234 
 + 56.7                  + 56700 
   57.934                  57934

　桁数を揃えるとは、桁の少ない方には桁の差の分だけ0をつけてやるということです。0をn個つけるということは要するに10n倍してやることを意味します。

　要するに固定小数点の加減算は計算前に桁揃えの処理をしてやれば、あとは整数演算がそのまま使えるわけです。


　かけ算の場合も同様です。小数のかけ算では小数点を無視して整数と思って計算して、あとから小数点桁を調整します。

1.234 × 56.7 = 69.9678

　この例なら1234と567をかけて、かける数が小数点以下3桁と1桁の数なので、結果の小数点以下3+1=4桁のところに小数点を打ちます。その理由は以下のようなことです。

1.234 × 56.7 = 1234 × 10-3 × 567 × 10-1 = 1234 × 567 × 10-(3+1)

　なお、かけ算の場合放っておいたらどんどん小数点以下桁数が増えていってしまうので、適宜丸める処理も必要になってきます。すなわち精度を保つのに必要な桁数よりも多くなった場合には、端数を切り捨てるなりしなければなりません。その場合の計算も簡単で、例えば3桁分切り捨てた場合は、103で割ってやればいいわけです。


　こういうやり方で固定小数点演算はもうできるわけですが、10進固定だと10nを掛けたり割ったりする処理が発生します。なぜそんな演算がいるかというとそれは桁を揃えたり切り捨てたりするためですが、そういう処理ならば2進小数にすればシフト演算を使うことで遙かに高速に行えます。


　2進小数とかいきなり出てきましたが、これまでの議論は位取り記数法の基本原理なので、何進法にも適用できます。単に10nとか書いていたところを2nと読み替えてやればいいだけです。


　というわけで固定小数点数xDを整数と2進小数点桁数のタプルで定義し、そのタプルを計算できるライブラリを作ってみたわけですが……

def setdigit(fd, nc):               #小数点位置を設定する
def matchdigit(x, y, nc=None):      #二つの固定小数点数の桁を揃える
def setint(n, nc):                  #整数nを指定桁数の二進固定小数に変換する
def tofloat(fd):                    #二進固定小数点数をdoubleに変換する
def toStr10(fd):                    #二進固定小数点数を十進小数文字列に変換する
def setfloat(f, nc):                #doubleを指定された二進桁数の固定小数点に変換する
def neg(x):                         #符号を反転する
def add(x, y):                      #二つの二進固定小数点数を加算する
def sub(x, y):                      #二つの二進固定小数点数を減算する
def mul(x, y, nc=None):             #二つの二進固定小数点数を乗算する
def div(x, y, nc=None):             #二つの二進固定小数点数を除算する

　―――そうしたらまるでアセンブラを書いてるみたいにクソ見づらい上、スピードも遅すぎてお話にならず、サンプルソースを出す気力も失せたので作った関数名だけを列挙しておきました。


桁数が同じと分かっている場合なら……

　しかしふて寝して翌日よく考えてみたら、そもそもそんなライブラリを作る必要なんてありませんでした。

　マンデルループ内の計算が発生するたびに関数を呼び出していたら、そりゃオーバーヘッドも効いてきます。

　そもそも異なった桁数の計算を想定していたことが間違っていて、最初から小数点以下桁数が同じ数値同士の計算と決めていれば、以下のような単純なルールで式を書けばよかっただけでした。


　すなわち、xD, yD を小数点以下d桁の固定小数点数、x, y をd桁目に小数点があるとみなして xD, yD を表した整数とすると……

◆加減算や比較を行う場合

　この場合は以下のように何も考えずに単にそうすればいい。

xD ＋ yD ＝ x ＋ y

xD － yD ＝ x － y

◆乗算を行う場合

　この場合は普通に乗算したあと、桁数分右シフトすればいい。

xD * yD ＝ x * y >> d

◆除算を行う場合

　この場合は被除数を桁数分左シフトしたあと、普通に整数除算すればいい。

xD // yD ＝ (x << d) // y

◆整数nとの計算の場合

　xDと整数nとの計算の場合は、乗除算は以下のようにそのままでよく、

xD * n ＝ x * n

xD // n ＝ x // n

　加減算や比較では nの桁を上げる。

xD ＋ n ＝ x ＋ (n << d)

xD － n ＝ x － (n << d)

　こうやってつくってみたのが以下のルーチンです。

import fdec

def icalc1(a0, b0, cmax, dig, C4):
    """多倍長整数で固定小数点を自前計算する
    
    a0,b0,cmax: 今までと同じ
    dig: 計算する値の小数点以下桁数
    C4: 定数4をあらかじめ指定桁に計算した値
    """
    x0, y0 = a0, b0
    xx0 = a0*a0 >> dig
    yy0 = b0*b0 >> dig
    for n in range(cmax):
        x1 = xx0 - yy0 + a0
        y1 = (2*x0*y0 >> dig) + b0
        xx0 = x1*x1 >> dig
        yy0 = y1*y1 >> dig
        if xx0 + yy0 > C4:
            break
        x0 , y0 = x1, y1
    return n

def mandel_i(data, aF, bF , pwF, zoom, iw, ih, cmax, calc):
    """16Lリストの自前固定小数点化

    data: 結果保存用のリスト
    aF,bF: 計算開始位置の座標(fdecタプル)
    pwF : ピクセルのサイズ(fdecタプル)
    zoom: 拡大率(この描画における小数点桁数の基礎となる)
    iw,ih: 計算する領域の幅と高さ(pixel)
    calc: 計算関数(a0, b0. cmax, dig, C4)
    """
    dig = zoom + 12      #計算の基本となる桁数(+8ビットくらいしてないと誤差が目立つ：脚注参照)
    C4 = fdec.setint(4, dig)[0]

    #基本的なパラメータを指定桁数で整数化
    a = fdec.setdigit(aF, dig)[0]
    b = fdec.setdigit(bF, dig)[0]
    pw = fdec.setdigit(pwF, dig)[0]

    for j in range(ih):
        b0 = b + pw*(ih-j)
        for i in range(iw):
            a0 = a + pw*i

            n = calc(a0, b0, cmax, dig, C4)

            data[j][i] = n

謎の速度バグ

　こうしてできたプログラムを見てみると、大元のcalc2のあちこちにちょっと >>dig がついているだけの超シンプルなものだったりするわけですが、作るのにえらく遠回りしてしまったのはこういうロジックを無意識に脳が拒否していたからかもしれません。


　というのも、これまでは精密な計算をする場合はdoubleを使うという癖が身に染みついていました。実際、圧倒的多くの場合はそれが正解です。

　その上、これまで使っていた整数は16ビットとか32ビットの幅しかなくて、かけ算が絡むとこんなアルゴリズムなら瞬時にオーバーフローして使い物になりません。

　そういうところがPythonでは無問題ということが頭では分かっていても、なかなか体がついてこないものなのです。そして同様の理由で別な問題にも直面しました。


　―――というのはプログラムが大体できたので、早速実行速度を測定しようとしているときでした。最初の印象ではかなり高速に動く様子だったので、勇んで色々パラメータを変えてみていたら、なぜか今度は異常に遅くなってしまったのです。


　おかしいと思って色々やってるうちに、なんだかループ回数の2乗に比例して時間がかかっていることが判明しました。例えばループ回数100回だと1秒そこそこで表示される画像が、ループ500回で計算すると5秒そこそこではなく、なぜか30秒くらいかかってしまうという謎現象に見舞われたのです。

　しかしマンデルループの計算速度は一定のはずです。従ってループ数を増やせば単にその回数に比例して計算時間は増えなければなりません。いったいどうやったらこんなことになるのでしょう？ どうしてループしていくと計算速度が遅くなっていくのでしょうか⁈


　私がどういうバグを仕込んでいたかというと……（ちょっと皆さんも考えてみてください。答えは反転のあとです）


　―――zoomパラメータにうっかりcmaxと同じ値を代入してました！


　1日くらい悩んで、ログを取ってみてびっくりです。

　zoomパラメータとは画面の倍率を指定する値で、それを元に小数点以下の精度を決めていました。またプログラムの開発中はループ回数cmaxを最小にしてデバッグしていました。


　そしてプログラムが正しく動作することを確かめてから、cmaxを500とか1000に増やしたわけですが―――そうすると、小数点以下の桁数がそれまでの100桁から500桁や1000桁に増えるわけです（桁数は2進法なので、10進法なら30桁くらいだったのが、150桁や300桁に増えたわけです）

　なおかつ1ピクセルのサイズは別に正しく計算して与えていたので見た目はまったく変わらず、結果としてループ回数に比例して小数点以下桁数が無駄に高精度な状態になっていたわけです。


　そして知る人ぞ知る、かけ算の計算量は桁数の2乗に比例します。従ってループ回数の2乗に比例して速度が遅くなってしまったのでしたｗ


　はっきり言ってこれまでなら悩むなんてあり得ないバグです。なぜならこんな間違いをしたらあっという間にオーバーフローするため、即座に露見してしまうからです。それゆえにそんな所に原因があるはずないと思ったのが完全な盲点で、Pythonのヤツはこれを実に律儀に計算してくれていたのでした。


　―――あとまた桁数と値を間違えて2のものすごい数乗を計算させてしまったときには、メモリをいきなり食いつぶしてしまってマシンがフリーズし、マウスカーソルまでがカクカクとしか動かなくなりました。何とか復帰した後もいろんなプロセスがスワップアウトしていてマシンが重くて動かず、結局リセットする羽目になってしまいました。

　というわけでPythonで整数を扱うときにはこんな注意も必要なのでした。


　さてそれはともかく最終的な結果を測定してみると……

描画時間: 8928.4 ms

　うーむ……calc0よりはずっと速いですが、calc1よりは遅いくらいのスピードです。


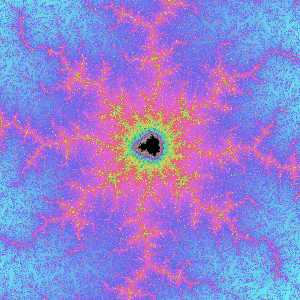
　しかし、前回モザイクになっていた画像が……


a=0.4345333081453485
b=-0.19884736127313102
pw=1.3877787807814457e-17

　今回はこのとおりです！


a=31311424714295372×2-56 b=-14328462434132468×2-56 pw=2-56

　真ん中にはこんな奴が隠れていました


a=500982795428728216×2-60 b=-229255398946117220×2-60 pw=2-60

もう少し速くするには

　さてそれはそうと精密な計算はできましたが、計算速度の方はかなり不足しているのは明白です。上のpw=2-60の画像を描くのに1分くらいかかってしまいます。昔は1時間近くかかっていたことに比べれば待てないことはない時間ですが、気持ちよくマンデル世界を周遊するとかはちょっと無理でしょう。


　そこでNumbaをかけてみると……

描画時間: 132.9 ms

　さすがNumba様！ でございます。


　それではまたマンデルブロ周遊に出かけようと部分を拡大していったときでした。


a=-4934802×2-22 b=1251946×2-22 pw=2-22

　倍率を一段上げてみると何だかゴミが出まくってるみたいですが……？


a=-9869454×2-23 b=2504042×2-23 pw=2-23

　もう一段上げたら画面が真っ暗に⁈


a=-19738758×2-24 b=5008234×2-24 pw=2-24

　実は最初のa=-4934802×2-22の画像はmandel_i関数のzoomパラメータに18が渡されていました。すると小数点以下の桁数はzoom+12になるので、この時点で小数点以下桁数が30になります。次がzoom=19なので桁数31、真っ黒なのはzoom=20で桁数32です。

　これはもうNumbaが多倍長整数に対応しておらず、整数演算には32ビットintを使ってるからだとしか言いようがありません。しかしjitにint64といったパラメータをつけてみても何だか上手くいかないようだし、そもそも現在doubleの52ビットまではちゃんと計算できている以上、本質的解決になりません。


　それではとCythonでもやってみましたが、こっちはもっとダメで、速度が2倍くらいにしかならない上、桁数16を越えたらメチャメチャになります。こっちは途中のかけ算のレベルでオーバーフローしているようです。


　えーっと―――こういう場合どうしたらいいんでしょうか？


望みは尽きたのか？

　ここで思い起こすのが複素数のときの話です。

　あのときPython組み込みの複素数型を使うと少しばかり速くなりました。それではPythonには組み込みの高精度の型は何かないでしょうか？


　そうやって見てみると―――Decimalというデータ型があります。これは10進数を精密に演算するためのデータ型のようですが、計算精度を任意に指定できるとあります。

　そこでこいつを使ってみたら……

描画時間: 39178.8 ms

　えーっと、まずもって話になりません。その上Numbaをかけてみても……

描画時間: 40651.2 ms

　まったく速度は向上しません。むしろ遅いくらいです。現在NumbaはDecimal型には対応していないようです。


　と、ここでいいアイデアが浮かびます。すなわち―――自前で多倍長整数演算の関数を作って、それをCythonでコンパイルしてみたらどうでしょうか？

　Pythonの場合多倍長演算はいろいろな計算に対応できなければなりませんが、ここで必要なのは加減算とかけ算だけです。それならば何とかなるのでは？

　そして1週間近くめっちゃ苦労した挙げ句……


Cythonで10倍速くはなりましたが、元のPythonレベルで30倍遅かったんで、結局3倍遅くなりました🖤

　Pythonの公式サイトのQ&Aにプログラムが遅すぎます。どうしたら速くなりますか？などという項目があります。そのなかにあったのが……

何かをするための基本要素が標準ライブラリにあるなら、自分で発明した代用品よりもそちらのほうが、(絶対にとは言えませんが) おそらく速いです。

　………………

　…………

　……

　整数演算という基本中の基本である以上、可能な限りの最適化がされていたのです。そんなところにシロートが手を出しても勝てるわけがなかったのでした。


　というわけで―――もはや望みは潰えたかに見えました。

　しかしまだ希望は失われていなかったのです。なぜならSpyderのステータスバーにはCPU使用率が常に表示されていたのです！ そしてそれを見るとこのPCが実は真の力の25％しか出していないことを如実に示していたのですから‼


　というわけで次回は並列処理編になります。


2017-05-06