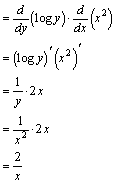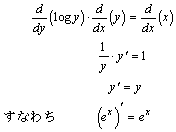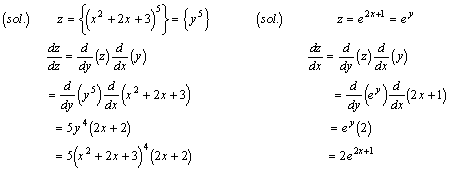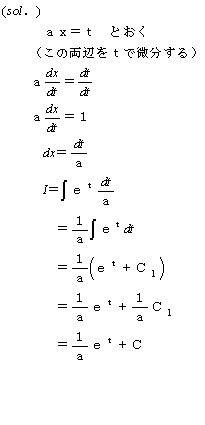侾丏懳悢娭悢偺旝暘
丂栤丂
倖(倶)亖log倎倶丂仺丂倖亴(倶)亖丠丂丂丂丂
旝暘偺暅廗丂丂

旝暘偺掕媊幃丂丂丂丂 丂
丂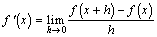 丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
椺戣(1)丂倖(倶)亖log倎倶丂仺丂倖亴(倶)亖丠乮sol.)丂丂丂
丂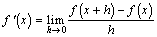 丂丂丂丂丂丂
丂丂丂丂丂丂
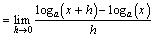 丂丂丂丂丂丂
丂丂丂丂丂丂
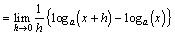 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
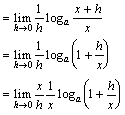 丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
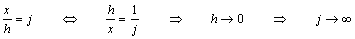 丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂
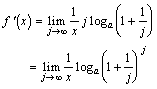 丂
丂丂丂丂丂丂
丂
丂丂丂丂丂丂
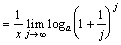 丂
丂
楙廗(1乯丂師偺幃偱丄倞亖侾侽丄侾侽侽丄侾侽侽侽丒丒丒偺偲偒偺抣傪億働僐儞丂丂丂丂丂
偱媮傔偰傒傛偆丅丂丂丂丂丂 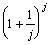 丂
丂
倞亖侾侽丂佀丂丂丂丂丂丂丂丂丂丂丂
丂倞亖侾侽侽丂佀丂丂丂丂丂丂丂丂丂丂丂
倞亖侾侽侽侽丂佀丂丂丂丂丂丂丂丂丂丂丂
倞亖侾侽侽侽侽丂佀丂丂丂丂丂丂丂丂丂丂丂
倞亖侾侽侽侽侽侽丂佀丂丂丂丂丂丂丂丂丂丂丂
倞亖侾侽侽侽侽侽侽丂佀丂丂丂丂丂
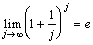 丂偲偍偔丂丂丂
丂偲偍偔丂丂丂
倕亖俀丏俈侾俉俀俉丏丏丏丏丏柍棟悢丂丂丂丂
乽暕堦敨擇敨丒丒丒乿丂丂丂丂
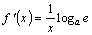
log倎倕亖侾丂偵偡傞偲, 曋棙偩丄偦偺偨傔偵偼丄倎亖倕丂偲偡傟偽傛偄丅
log倕倕亖侾掙偑倕偺懳悢丂log倕倶丂傪乽帺慠懳悢乿偲偄偄丅掙傪徣棯偟偰丄扨偵log丂倶丂偲偐丂ln丂倶丂偲昞偡丅丂丂丂
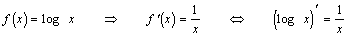 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂
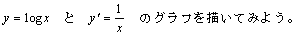 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂
慻丂丂弌惾斣崋丂丂巵柤
俀丏巜悢娭悢偺旝暘丂丂丂丂丂丂
崌惉娭悢偺旝暘丂丂丂
倸丂丂仼丂丂倷丂仼丂倶丂丂丂丂丂 丂丂丂
倸亖倸(倷)丄倷亖倷(倶)丂丂丂丂丂丂丂丂丂丂
倸亖倸(倷(倶))丂丂丂丂丂丂丂丂丂丂丂丂
倸丗倶丆倷偺崌惉娭悢丂丂丂
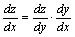 丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂
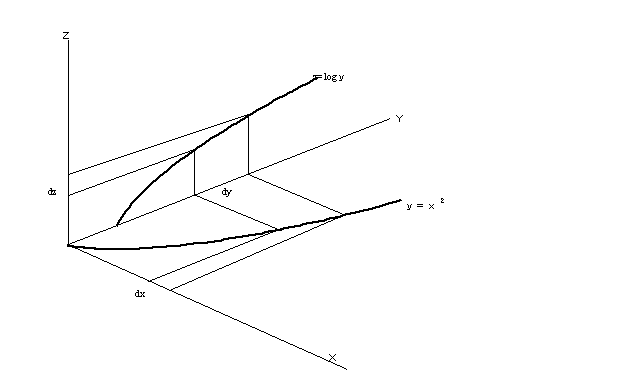
椺丟倸丂丂仼丂丂倷丂仼丂倶丂
倸亖log倷丄 倷亖倶俀丂
丂
倸亖log(倶俀)
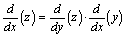 丂
丂丂
丂
丂丂
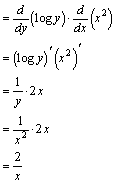
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
椺戣乮俀乯丂丂丂倷亖倕倶丂丂 佀丂倷亴亖丠
丂 |
|
丂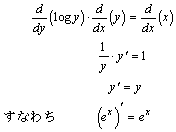 |
|
丂帺慠懳悢偺掙倕傪掙偲偡傞巜悢娭悢偺摫娭悢偼丄尦偺娭悢偲偍側偠偵側傞丅丂
懄偪丄倕倶丂偼旝暘偟偰傕曄傢傜側偄娭悢偱偁傞丅
椺戣(俁)丂乷(倶俀亄俀倶亄俁)俆}亴亖丠丂丂丂丂椺戣(係)
(倕俀倶亄侾)亴 亖丠
峫偊曽丟倸亖倷俆丄倷亖倶俀亄俀倶亄俁丂丂丂峫偊曽丟倸亖倕倷
丄倷亖俀倶亄侾丂丂丂
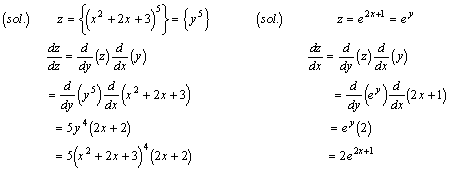
楙廗(2)丂師偺娭悢傪崌惉娭悢偺旝暘岞幃傪梡偄偰旝暘偣傛丅
(1)丂乷(倶俀亄侾)係}亴丂丂丂丂丂丂丂丂丂
(2) (倕亅倶)亴丂丂丂丂丂丂丂丂
(3)丂(倕倶亄倕亅倶)亴丂丂丂丂丂丂丂丂丂丂
(4) 乷(俀倶亄侾)俁}亴丂丂丂丂丂丂丂丂
(5)丂乷(倶俁亄倶亅俁)俀}亴丂丂丂丂丂丂丂
(6) (倕亅俲倶)亴丂丂丂丂丂丂丂丂
(7)丂倷丟曻幩惈暔幙偺検丆丂丂丂丂丂丂丂丂丂
倶丟帪崗丄們丆兩丟掕悢丂丂丂丂丂丂丂倷亖們倕亅兩倶丂佀丂倷亴丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
慻丂丂弌惾斣崋丂丂巵柤
俁丂巜悢娭悢偺愊暘丂丂丂丂丂
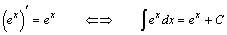 丂
丂

丂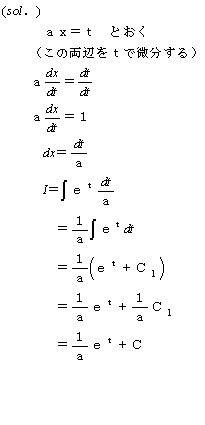
丂丂愊暘掕悢傪嵟廔揑偵偼俠偵偡傞偨傔丂偵搑拞偵弌偰偔傞愊暘掕悢傪俠侾
偲偟丂偨丅
丂 |
|
|
丂丂
丂丂
丂丂丂丂偲偍偄偰丄偡偭偒傝偟偨
丂丂丂宍偵偟偰偄傞丅 |
|
|
丂丂丂慻丂丂丂弌惾斣崋丂丂巵柤
係丏旝暘曽掱幃丂
棊壓懍搙丂
変乆偼丄侾妛婜偵婛偵丄暔懱偺棊壓偵娭偟偰丄師偺宍偺旝暘曽掱幃傪妛傫偩丅丂丂丂
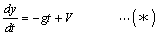 丂
丂
斀墳懍搙丂
擹搙偺偆偡偄僔儑摐悈梟塼偺揮壔斀墳傪挷傋偰傒傛偆丏偙偺斀墳偼偮偓偺斀墳幃偱昞偝傟傞丏丂丂丂
俠12H俀俀俷11亄俫俀侽仺俠俇俫侾俀俷俇亄俠俇俫侾俀俷俇丂丂乮僔儑摐乯丂丂丂丂
乮僽僪僂摐乯乮壥摐乯斀墳偺恑峴拞偵偍偘傞悈偺擹搙偼堦掕偲傒側偟丆怗攠偲偟偰巊傢傟傞墫巁傕丆
斀墳偺慜屻偱擹搙偼曄壔偟側偄偲傒側偡丏丂
斀墳偺巒傔偵偍偄偰丆僔儑摐偺擹搙傪a[mol/噂乴偲偡傞丏
斀墳奐巒屻倲[昩]傪宱夁偟偨偲偒傑偱偵丆倶(倲)[mol乛噂]偩偘暘夝偟偨偲偡傞偲丆僔儑摐偺擹搙偼丂丂丂
乮a亅倶)[mol/噂乴偵側偭偰偄傞丏
僔儑摐偺暘夝検倶(倲)[mol/噂乴偼帪娫偺娭悢偵側傞偐傜丆暘夝懍搙偼丂丂丂
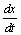
偱昞偝傟傞丏
幃偐傜傢偐傞傛偆偵丆偙傟偼僽僪僂摐偍傛傃壥摐偺惗惉懍搙偱傕偁傞丏
偙偺傛偆側斀墳偱偼丆斀墳懍搙偼斀墳偟偰偄傞暔幙偺擹搙偵斾椺偡傞偲峫偊傜傟傞偐傜丆
斾椺掕悢傪倠偲偟偰丆偮偓偺幃偱昞偝傟傞丏丂丂丂
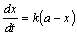 丂
乮侾乯丂丂丂丂丂丂丂丂丂丂丂丂丂
丂
乮侾乯丂丂丂丂丂丂丂丂丂丂丂丂丂
丂
曻幩惈暔幙偺曵夡丂
幚尡偵傛傞偲丆曻幩惈暔幙偺尨巕妀偑曵夡偡傞懍偝偼丆偁傞弖娫偵曵夡偟側偄偱巆偭偰偄傞尨巕妀偺悢偵斾椺偡傞丏
偁傞帪崗倲偵偍偗傞曻幩惈暔幙偺尨巕妀偺悢傪帪娫偺娭悢俶(倲)[屄]偲偡傟偽丆曵夡偺懍偝偼丄尭彮棪傪昞偡偺偱偁傞偐傜丆丂丂丂

偲側傞丏偙傟偑尰嵼検俶(倲)[屄]偵斾椺偡傞偺偱偁傞偐傜丆斾椺掕悢傪兩偲偡傟傁丆媮傔傞幃偼丂丂丂
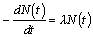 乮俀乯 丂丂丂丂丂丂丂丂丂
乮俀乯 丂丂丂丂丂丂丂丂丂
偲側傞丏丂丂
徃壺懍搙丂丂
僫僼僞儕儞偺幙検倣偼丆徃壺偵傛偭偰丄偦偺昞柺愊俽偵斾椺偟偰尭彮偡傞偙偲偑抦傜傟偰偄傞丏
偲偙傠偱丄幙検倣偼丄枾搙兿偲懱愊倁偺愊兿倁偱偁傞偐傜丄幙検倣偺曄壔偼丄偡側傢偪懱愊倁偺曄壔偵側傞丅丂
廬偭偰丄僫僼僞儕儞偺懱愊倁偼丄偦偺昞柺愊俽偵斾椺偟偰尭彮偡傞偲尵偄姺偊傜傟傞丅
僫僼僞儕儞媴偺懱愊倁偺尭彮傪昞偡娭學幃偼偳偺傛偆偵側傞偐丏丂
帪崗倲[帪娫]偺偲偒丄懱愊倁偼帪崗倲偺娭悢側偺偱倁(倲)丄昞柺愊俽傕帪崗倲偺娭悢側偺偱丄俽(倲)丂丂丂丂

偨偩偟丄倁(倲)偲俽(倲)偺娫偵偼丄壓偺娭學偑偁傞丅丂丂丂丂
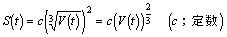 丂
丂
丂忋幃乮侾乯乮俀乯乮俁乯偺傛偆偵丆曄壔懍搙偑丆尰嵼懚嵼偟偰偄傞検偵傛偭偰婯掕偝傟傞傛偆側帠徾偼帺慠奅偵傕懡偄丏
丂乮仏乯幃偵傆偔傑傟偰偄傞倲偺娭悢倷丄
乮侾乯幃偵娷傑傟偰偄傞倲偺娭悢倶(倲)丄
乮俀乯幃偺俶(倲)丄
乮俁乯幃偺倁(倲)
偼丆偳傫側娭悢偱偁傞偐傑偩傢偐偭偰偄側偄偐傜丆枛抦娭悢偱偁傞丏
偙偺傛偆偵丆曄悢丆枹抦娭悢丆枛抦娭悢偺摫娭悢傪娷傫偱偄傞曽掱幃傪旝暘曽掱幃偲尵偭偨丅丂
曄壔偡傞帠徾傪夝柧偟傛偆偲偡傞応崌偵棙梡偝傟傞丅
旝暘曽掱幃傪枮懌偡傞枹抦娭悢傪媮傔傞偙偲傪丆旝暘曽掱幃傪夝偔偲尵偭偨丅丂丂丂
丂俆丏旝暘曽掱幃偺夝朄丂

丂
丂 |
|
|
丂丂慻丂丂弌惾斣崋丂丂巵柤丂
俇丏旝暘曽掱幃偺嬶懱揑夝朄丂
丂楙廗(俇)丂曻幩惈暔幙偺幙検倣偼帪娫倲偺娭悢偱偁傞丅
丂丂丂丂倣亖f(t)
丂帪崗倲偵偍偗傞倣偺尭彮棪亅倣亴偼丄
偦偺帪崗倲偵偍偗傞幙検倣偵斾椺偟偰偄傞丅

倲亖侽丂偺偲偒丂倣亖俵丂偱偁偭偨丅丂丂丂丂乮弶婜忦審乯丒丒丒嘇
倣亖倖(x)偺娭悢宍傪媮傔傛丅
丂丂
丂 |
|
椺戣(俉)丂曻幩惈暔幙偼帪娫偲偲傕偵幙検傪尭傜偟偰偄偔丅
丂嵟弶偺幙検偑敿暘偵側傞婜娫傪乽敿尭婜乿偲偄偆丅
丂嵟弶偺幙検傪俵偲偟丄敿尭婜傪俿
偲偡傞偲丄楙廗乮俇乯偱摼偨幃偼偳偺傛偆偵側傞偐丅

丂
|
|
丂丂
楙廗乮俈乯丂暔幙俙偑暘夝偟偰丄暔幙俛偵曄壔偡傞偲偒丄暔幙俙偺擹搙們偼丄帪娫倲偺娭悢偱偁傝丄擹搙們偺帪崗曄壔棪亖斀墳懍搙偼丄擹搙們偵斾椺偡傞丅
弶婜忦審丟倲亖侽偺偲偒丄們亖們侽丂丒丒丒嘇
擹搙們偺娭悢宍傪媮傔傛丅乮擹搙丟concentration[遁据内布]乯
側偍丄愊暘掕悢偵偼俲傪巊偆偲傛偄丅丂丂丂
慻丂丂弌惾斣崋丂丂巵柤丂
楙廗(俉)丂丂丂丂
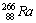 丂儔僕僂儉俼倎偺敿尭婜偼侾俇侽俀擭偱偁傞丅嵟弶偺堦擭娫偱丄侾侽侽倗偺俼倎偼壗倗偵側傞偐丅椺戣(俉)傪嶲徠偟偰夝偗丅丂丂丂丂
丂儔僕僂儉俼倎偺敿尭婜偼侾俇侽俀擭偱偁傞丅嵟弶偺堦擭娫偱丄侾侽侽倗偺俼倎偼壗倗偵側傞偐丅椺戣(俉)傪嶲徠偟偰夝偗丅丂丂丂丂
楙廗(俋)丂丂丂
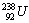 丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂 
丂僂儔儞倀娷桳峼愇偺拞偵僂儔儞侾倗偵懳偟偰墧Pb偑侽.俉俆倗偁偭偨丅偙偺墧Pb偼僂儔儞倀偑曵夡偟偰弌棃偨傕偺偱偁傞丅
偙偺峼愇偑弌棃偰偐傜壗擭宱夁偟偨偐丠偨偩偟丄僂儔儞倀偺敿尭婜偼係.俆侾亊侾侽俋擭偱偁傞丅丂丂
慜偺儁乕僕偵栠傞
尦偺儁乕僕偵栠傞
Home Page
 丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
 丂
丂丂丂丂丂丂
丂
丂丂丂丂丂丂