公務員試験に出る三角形の魔方陣の問題

三角形の魔方陣の問題(一辺に３個の数字)

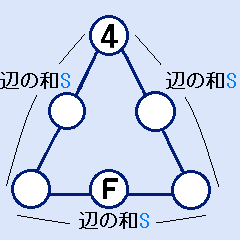右図は、初級公務員試験の類題です。「1～6の異なる整数を図の○の中に入れ、各辺ごとにその上にある３つの整数の和が、すべて等しくなるようにします。このとき、Fには２種類の整数が入りますが、それらの和はいくらですか。」

（一つの頂点だけに４の数字が入っています）

答：Fの２種類の整数の和は４です。

辺の和は示されていませんが、解が存在するのは、辺の和＝9,10,11,12の時だけです。三角形の魔方陣(一辺に３個の数字)は辺の和が決まれば、解は１種類ですから、Fに２種類の整数が入るというのは、辺の和により、Fの値が２種類あるという事を意味します。

三角形の魔方陣(一辺に３個の数字)の解答に見られるように、頂点に４の数字が入るのは、辺の和Sが11と12の場合です。

三角形の魔方陣の問題(一辺に４個の数字)

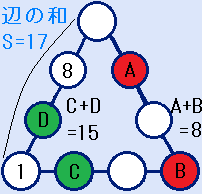上図の九つの○に1～9の異なる整数を入れて、三角形の各辺上の四つの整数の和（辺の和S）がいずれも17になるようにします。1と8はすでに図の位置に入っています。

Ａ＋Ｂ＝８。Ｃ＋Ｄ＝１５。の条件で、Ｂ＋Ｄの値を求めてください。

答：Ｂ＋Ｄ＝９

三角形の魔方陣の問題(一辺に４個の数字)解き方

定められた条件のうち、一直線上にある辺の和S=17とＡ＋Ｂ＝８に注目します。

一番上の頂点ｅには7は入れない

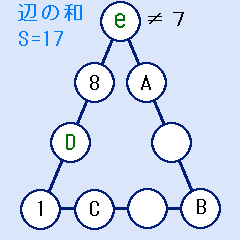辺の和S=17ですから、e+D=8です。

ここでe=7とすると、D=1となり、1が重複してしまいます。よって、一番上の頂点eには7は入れません。

Ａ＋Ｂ＝８

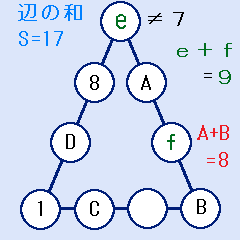Ａ＋Ｂ=８なので、ｅ＋ｆ=９です。

すでに使われている１、８を除き、また、e=7を除けば、和が９になるのは（ｅ,ｆ）=（2,7）、（3,6）、（4,5）、（5,4）、（6,3）です。

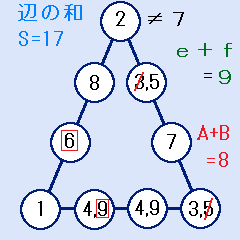• （e,f）=（2,7）の時、D=6となり、残りの数字でＡ＋Ｂ＝８にするには、（Ａ,Ｂ）=（３,５）か（５,３）です。どちらにしろ、後の残りの数字は４と９で、これが底辺に入ります。

  1. 右下隅のＢに５が入ると、底辺の数字の和＝19となって不適です。
  2. よって、右下隅のＢに３が入ります。Ｃ＋Ｄ＝１５の条件から、Ｃには９が入ります。答：Ｂ＋Ｄ＝３＋６＝９
• （e,f）=（3,6）の時、D=5となり、残りの数字でＡ＋Ｂ＝８にする事はできないので不適です。
• （e,f）=（4,5）の時、D=4となり、４が重複するので不適です。

• （e,f）=（5,4）の時、D=3となり、残りの数字でＡ＋Ｂ＝８にするには、（Ａ,Ｂ）=（２,６）か（６,２）です。

  どちらにしろ、後の残りの数字は７と９で、底辺の数字の和が17を超えるので不適です。

• （e,f）=（6,3）の時、D=2となり、残りの数字でＡ＋Ｂ＝８にする事はできないので不適です。

三角形の魔方陣の問題(一辺に４個の数字)の答

最終結果は下図のようになります。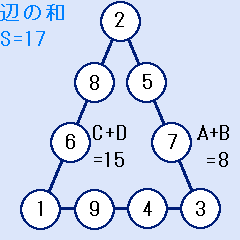

三角形の魔方陣を解く上での注意点

一番上の頂点の数字をXとして、X+8+D+1=17。右のAの下の空欄をYとして、X+A+Y+B=17。等として、連方程式を解くという方法は、良くない。何故なら、これらの方程式には、1≦X≦9の条件が含まれないので、X=-5なども許されてしまうからです。