公務員試験に出る五芒星の魔方陣の問題
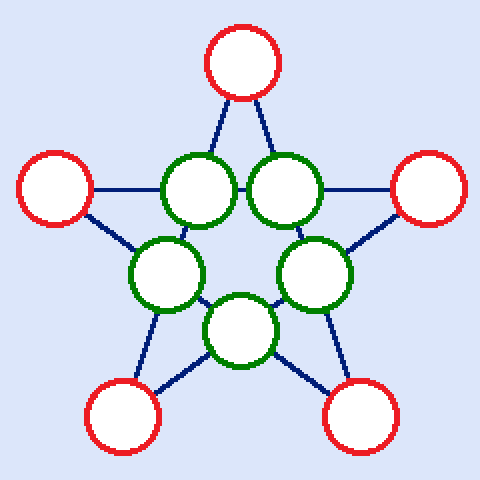 五芒星の魔方陣とは、五芒星の頂点と交点(全部で10か所)に異なる整数を入れ、直線上の4個の数字の和Sが全て同じになるようにするものです。星型魔方陣とも言います。
五芒星の魔方陣とは、五芒星の頂点と交点(全部で10か所)に異なる整数を入れ、直線上の4個の数字の和Sが全て同じになるようにするものです。星型魔方陣とも言います。
ただ、1から10までの連続した整数での解はありません。1から12の連続した整数のうち、7と11を除いた1,2,3,4,5,6,8,9,10,12を使った場合は、解があります。
1,2,3,4,5,6,8,9,10,12を使った星型の魔方陣の問題
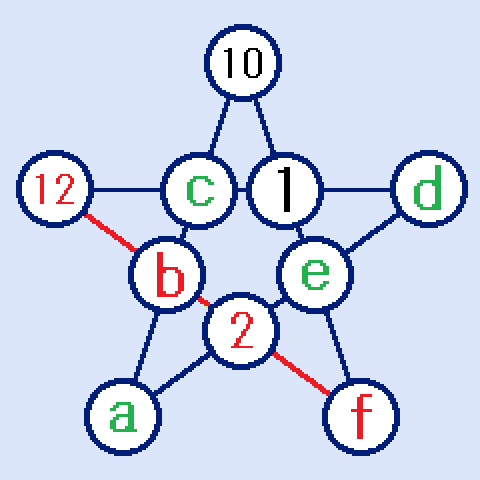 1,2,10,12はすでに埋め込まれています。残りの数字3,4,5,6,8,9をa~fに入れて下さい。ただし、4個の数字の和S=24という条件つきです。
1,2,10,12はすでに埋め込まれています。残りの数字3,4,5,6,8,9をa~fに入れて下さい。ただし、4個の数字の和S=24という条件つきです。
条件を式にすると、以下のように式は5つ、変数は6つですから、単純に連立方程式を解くという方法では答は出ません。
- 12+c+1+d=24
- d+e+2+a=24
- a+b+c+10=24
- 10+1+e+f=24
- f+2+b+12=24
星型魔方陣の解き方
f+2+b+12=24ですから、f+b=10です。残りの数字3,4,5,6,8,9で、足して10になるのは(b,f)=(4,6)か(6,4)です。
b=4,f=6の場合
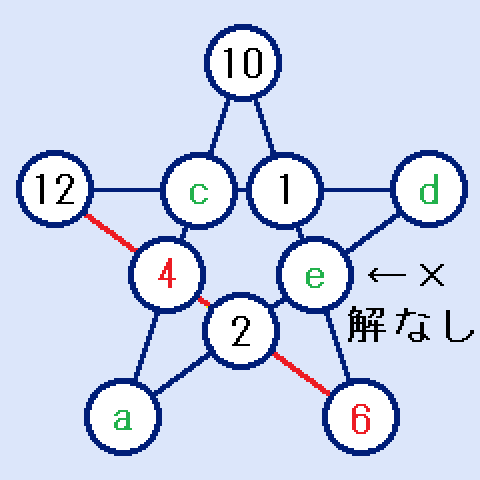 b=4,f=6を入れた状態が右図です。
b=4,f=6を入れた状態が右図です。
10+1+e+6=24からe=7ですが、7は使えません。よって、b=4,f=6の場合は、解なしです。
b=6,f=4の場合
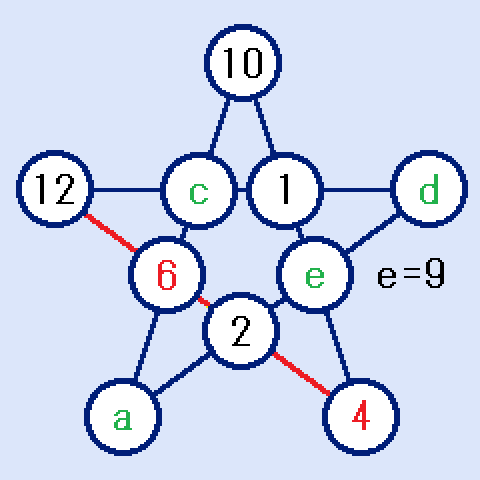 b=6,f=4を入れた状態が右図です。10+1+e+4=24からe=9です。
b=6,f=4を入れた状態が右図です。10+1+e+4=24からe=9です。
12+c+1+d=24からc+d=11です。残りの数字3,5,8で、足して11になるのは、(c,d)=(3,8)か(8,3)です。
- c=8の場合。a+6+8+10=24からa=0となり、不適です。
- c=3の場合。a+6+3+10=24からa=5となり、d=8となりますが、これは解です。
解は下図のようになります。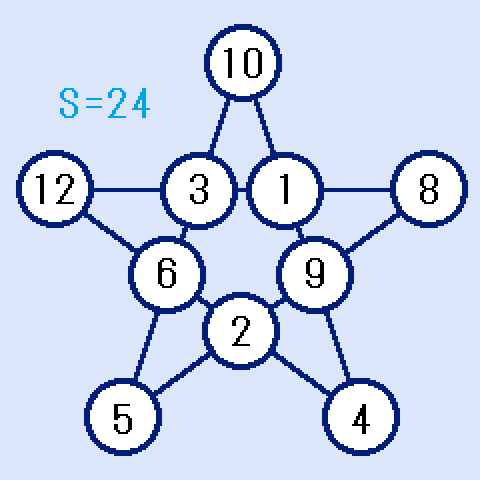
最後まで読んでいただいて、ありがとうございました。
