五芒星と六芒星の魔方陣の問題と解き方
五芒星の魔方陣
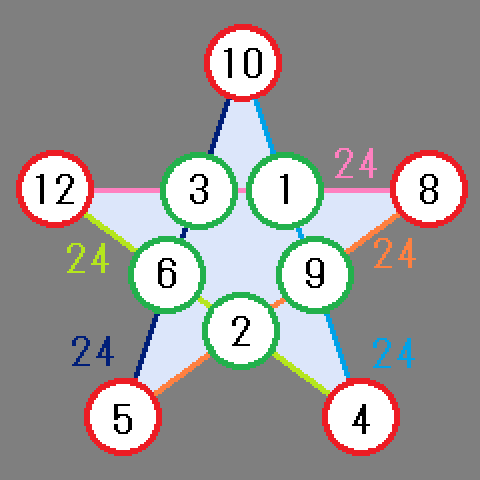 五芒星の魔方陣とは、五芒星の頂点と五芒星の辺の交点に異なる整数を入れ、辺上の4個の数字の和が全て同じになるようにするものです。星型魔方陣とも言います。
五芒星の魔方陣とは、五芒星の頂点と五芒星の辺の交点に異なる整数を入れ、辺上の4個の数字の和が全て同じになるようにするものです。星型魔方陣とも言います。
しかし、1から10までの連続した整数での解はありません。1から12の連続した整数のうち、7と11を除いた1,2,3,4,5,6,8,9,10,12を使った場合は、解があります。(右図)
五芒星の魔方陣の問題
1,2,3,4,5,6,8,9.10,12の数字を1回ずつ入れて、五芒星の辺の4個の数字の和が全て同じになるようにします。ただし、2,6,3,9はすでに入っています。確定していない所をA,B,C,D,E,Fとしました。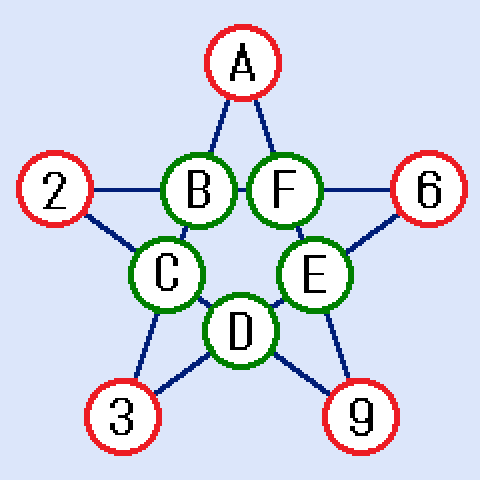
五芒星の魔方陣の解き方
魔方陣の問題を解く時に最初にする事は、五芒星の辺の4個の数字の和を求める事です。その和をSとします。
s=24
- s=A+B+C+3
- s=3+D+E+6
- s=6+F+B+2
- s=2+C+D+9
- s=9+E+F+A
上記の5つの式を辺々足すと、5S=2(A+B+C+D+E+F+2+3+9+6)=120で、s=24となります。
B,Fの数字を絞り込む
2,B,F,6の辺に注目すると、2+B+F+6=24ですから、B+F=16です。すでに入っている2,6,3,9を使わないで、足して16になる2組の異なる数字は4と12だけです。(B,F)=(4,12)か(12,4)に絞り込めました。
(B,F)=(4,12)の場合
A,F,E,9の辺で、Fに12を入れるとA+E=3ですが、2がすでに使われているのでA+E=3にはなれません。
(B,F)=(12,4)の場合
Bに12、Fに4を入れたのが下図です。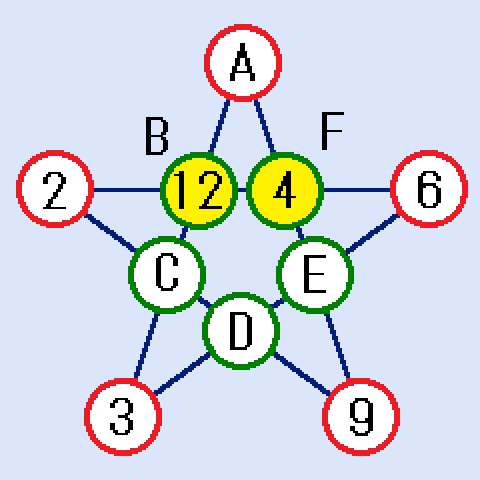
A,F,E,9の辺で、Fに4を入れるとA+E=11ですが、足して11になる2組の異なる数字は1と10だけです。
Aに1を、Eに10を、Dに5を、Cに8を入れると、下図の解答になります。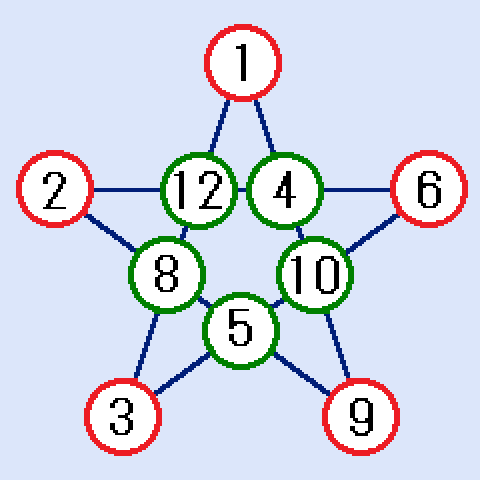
六芒星の魔方陣
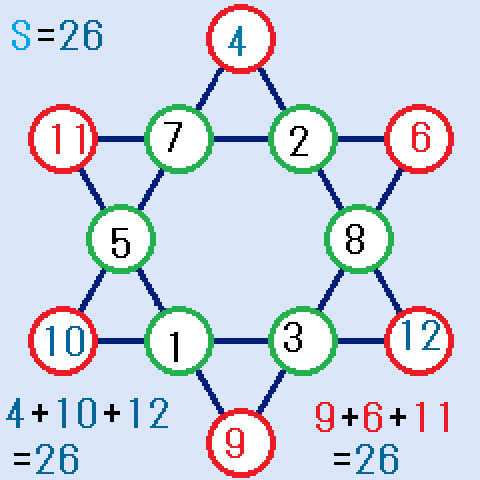 六芒星の魔方陣とは、六芒星の頂点と交点(全部で12か所)に1から12の整数を入れ、直線上の4個の数字の和Sが全て同じになるようにするものです。
六芒星の魔方陣とは、六芒星の頂点と交点(全部で12か所)に1から12の整数を入れ、直線上の4個の数字の和Sが全て同じになるようにするものです。
右の図は、さらに、上向きの正三角形△の頂点の数字の和、下向きの正三角形▽の頂点の数字の和も、直線上の4個の数字の和Sと同じになっています。
六芒星の魔方陣の問題
1から12の数字を1回ずつ入れて、六芒星の辺の4個の数字の和が全て同じになるようにします。ただし、4,6,9,11,12はすでに入っています。確定していない所をA,B,C,D,E,Fとしました。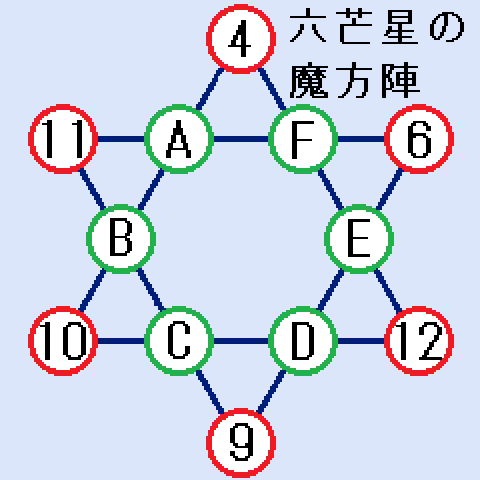
六芒星の魔方陣の解き方
魔方陣の問題を解く時に最初にする事は、六芒星の辺の4個の数字の和を求める事です。その和S=26になります。求め方は五芒星の時と同じで、1から12までの和=78なので、S=78×2÷6=26という計算で求まります。
連立方程式では解けない
六芒星の辺の4個の数字の和=26を6つの辺に適用すると、以下の6つの連立方程式ができます。
- A+B=12
- B+C=6
- C+D=4
- D+E=11
- E+F=10
- F+A=9
式が6つ、変数が6つですから、解けると思いきや、解が複数出てしまいます。例えば、A=7,B=5,C=1,D=3,E=8,F=2、A=8,B=4,C=2,D=2,E=9,F=1、A=9,B=3,C=3,D=1,E=10,F=0などです。これは、上の連立方程式に「全ての変数は異なる、また、全ての変数は1から12の自然数である」という条件が含まれていないからです。
C、Dに入る数字を場合分けする
10と12を結ぶ辺の4個の数字の和を考えると、C+D=4です。異なる2つの数字の和が4になるのは、1と3だけです。
- (C,D)=(3,1)の場合。4個の数字の和=26から、Bに3を入れる事になりますが、3が重複してしまうので解にはなり得ません。
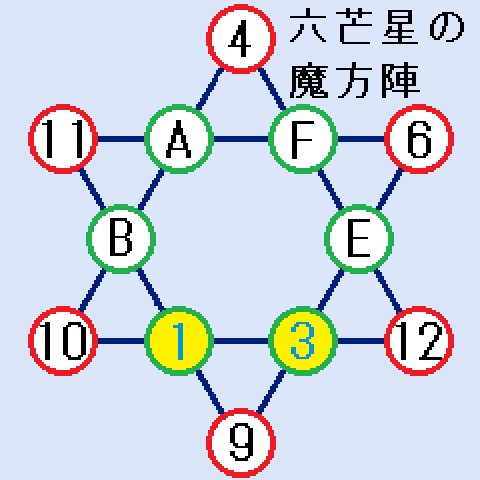 (C,D)=(1,3)の場合。Cに1、Dに3を入れたのが右図です。
(C,D)=(1,3)の場合。Cに1、Dに3を入れたのが右図です。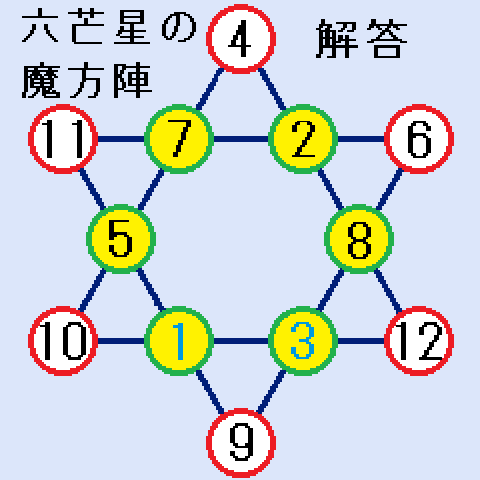 4個の数字の和=26から、順にB=5、A=7、F=2、E=8と決まります。右図が解答です。
4個の数字の和=26から、順にB=5、A=7、F=2、E=8と決まります。右図が解答です。
最後まで読んでいただいて、ありがとうございました。
