2009年7月7日 火曜日 8:39:31 PM 当サイトの基本的な分析手法の概要を説明します。
トレンドの予測 1
Step 1 株価の日次終値時系列データは一般的にランダムに変動していると見なされる。故に、当サイトが開発した方法で株価を近似し、株価のトレンドを決定します。
近似された株価トレンドを“CP近似”と呼び、CP近似を、CP長波、CP中長波、CP中波、CP短中波、CP短波、CP超短波、CPマイクロ波に分類する。
Step 2 CP近似を用いてトレンド予測を行なうと、直近のトレンドの影響を過度に受けがちなので、
株価トレンドという非定常波を、一定の範囲内で変動している定常波へ変換して、直近のトレンドの影響を過度に受けないようにする。
定常波を得る為、当サイトが開発した確定粒子を各CP波から導出し、確率に変換する。これを株価の“位置確率”と呼ぶ。
Step 3 確率に変換されている時間領域(time domain)にある各CP波の確定粒子(位置確率)はノイズの多いランダムな定常波なので、
位置確率を離散フーリエ変換(DFT: Discrete Fourier Transform)により周波数領域(frequency
domain)へ変換してスペクトル(spectrum)を得る。
Step 4 スペクトルからノイズ成分を除去し、離散逆フーリエ変換(discrete inverse Fourier transform)により時間領域へ変換する。これを株価の“位置確率波動”と呼ぶ。
Step 5 当サイトが開発した予測手法を用いて、位置確率波動の予測値を得る。
Step 6 定常的な位置確率波動と予測値を非定常波へ変換し、各CP波と予測部分の近似値を得る。これを株価の“CPS近似”と呼び、株価トレンドの予測を得る。
予測部分を含むCPS近似は、過去のトレンドよりも周期変動の影響の方を大きく受ける。CPS近似を、CPSマイクロ波、CPS超短波、CPS短波、CPS短中波などに分類する。
トレンドの予測 2
Step B1 各CP波の速度を確率へ変換する。
Step B2 確率に変換されている時間領域にある各CP波の速度を離散フーリエ変換により周波数領域へ変換してスペクトルを得る。
Step B3 スペクトルからノイズ成分を除去し、離散逆フーリエ変換により時間領域へ変換する。これを株価の“速度波”と呼ぶ。
Step B4 速度波がプラスならば上昇トレンド、マイナスならば下降トレンドなので、速度波の符号の転換が近いかを識別し、トレンドの変化の兆候を探知する。
Step B5 当サイトが開発した予測手法を用いて、速度波の予測値を導出し、速度波に周期の崩れが生じ、トレンドの発生または継続の兆候があるか分析する。
位置確率波動の予測部分の不確定さは速度波の不確定さより小さいという利点がある一方、速度波は周期の崩れを探知する点で勝っている。
Step B6 定常的な速度波と予測値を非定常波へ変換し、各CP波と予測部分の近似値を得る。これを株価の“CPV近似”と呼び、株価トレンドの予測を得る。
CPV近似は、CPVマイクロ波、CPV超短波、CPV短波、CPV短中波などに分類される。
離散データのフーリエ変換に関するサンプリング定理に関して
一関厚文
2009年7月20日
フーリエ変換では離散的な時刻にデータを取得する事を“サンプリング”と呼んでいます。
サンプリングする際にデータを、例えば2秒間に1000回取得するとします。
データを取得している時間または期間を、ここでは“サンプリング時間”と呼びT で表わすことに
しましょう。(この例では、サンプリング時間は2秒なので T=2)
サンプリング時間にサンプリングする回数を単に“データ数”と呼びN で表わしましょう。
(この例では、データ数は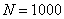 ) 一方、サンプリング時間にサンプリングする間隔は ) 一方、サンプリング時間にサンプリングする間隔は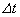
と表わされ、“サンプリング周期”と一般的に呼ばれています。
(この例では、サンプリング周期は 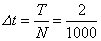 なので、 0.002秒となります) なので、 0.002秒となります)
サンプリング周期の逆数はサンプリング周波数と呼ばれており、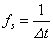 で表記することが で表記することが
出来ます。(この例では、サンプリング周波数は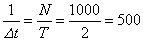 となり、 となり、
1秒間にサンプリングする回数を表わします) この様にサンプリングされた離散データを、
フーリエ変換することは離散フーリエ変換と呼ばれています。実質的に、
離散フーリエ変換とは、時間領域にある離散データを周波数領域へと変換する事を意味します。
その際に重要な概念の一つにナイキスト周波数というものがあり、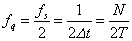
で与えられています。ナイキスト周波数とは離散フーリエ変換の周波数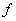 の有効範囲を示す の有効範囲を示す
周波数で“エイリアシング (aliasing)”と呼ばれる現象を避ける基準となります。
エイリアシングとは、連続信号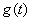 のフーリエ変換 のフーリエ変換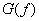 がナイキスト周波数より がナイキスト周波数より
大きな範囲(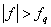 )において0でないなら、離散データ )において0でないなら、離散データ に対するフーリエ変換 に対するフーリエ変換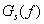 が が
連続信号のフーリエ変換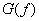 からずれてしまう現象の事です。端的に言うと、 からずれてしまう現象の事です。端的に言うと、
連続信号からサンプリングされた離散データのスペクトルが連続信号のスペクトルから
ずれてしまうというエイリアシング現象を避けるためには、離散フーリエ変換の周波数は
ナイキスト周波数の範囲内でのみ有効でなければならないということです。
下のグラフはエイリアシング現象の一例です。
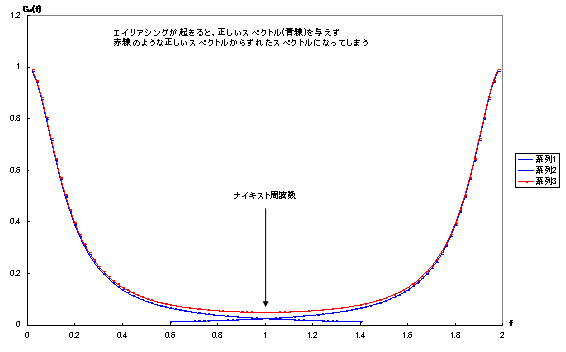
上のグラフから分かるとおり、正しいスペクトルを得るには、ナイキスト周波数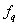 が が
より広範囲の周波数をカバーしなければなりません。ナイキスト周波数は 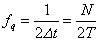
で与えられるので、ナイキスト周波数を大きくするには、与えられたサンプリング時間T において、
サンプリング周期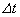 を短くしデータ数N を増やすか、またはデータ数N を変えずに、 を短くしデータ数N を増やすか、またはデータ数N を変えずに、
サンプリング周期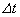 とサンプリング時間T を短くすれば良い。 とサンプリング時間T を短くすれば良い。
(上の例では、例えば T=2 を 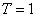 に変える) に変える)
以上がサンプリング定理が実質的に意味するところです。
これは、日次データの株価の場合には何を意味するのでしょうか?
サンプリング時間を営業日数と定義するなら、サンプリング時間を一定にすると、日次データ数も
変わらず、サンプリング周期も一定のままなので、ナイキスト周波数に変化はありません。
一方、サンプリング時間を短くしても、日次データ数もその分少なくなり、サンプリング周期も
一定のままなので、やはりナイキスト周波数に変化はありません。それで、日次データが取られた
任意のサンプリング時間を一単位とする新たな時間単位T を定義し, 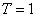 に於ける に於ける
日次データ数N を得る。N を一定にしたままナイキスト周波数を大きくしたい場合は、
サンプリング時間を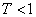 と技術的に短くすることで、サンプリング周期も短く出来る。 と技術的に短くすることで、サンプリング周期も短く出来る。
一方、サンプリング時間を一定にしたままナイキスト周波数を大きくしたければ、
日次データ数を増やす事により、サンプリング周期を短く出来る。これら2つの手法により、
離散フーリエ変換によるスペクトルがフーリエ変換のスペクトルからずれてしまうエイリアシングを
避けて、より良い近似を得ることが出来る。以上の事から分かるとおり、スペクトル分析によると
株価の日次データには営業日という時間概念以上に重要な時間の概念があるということです。
N225 CPS Shortwave T=4 〜 T=0.05 のグラフでは、エイリアシングが起きると、
離散フーリエ変換によって近似された株価トレンドが如何に株価と乖離していくか、また、
サンプリング時間を技術的に短くしてエイリアシングを避けると、離散フーリエ変換によって
近似された株価トレンドが如何に良く株価を近似するかを示しています。
T=4 と T=2 は明らかに株価と乖離しており、エイリアシングが起きている事が分かる。
T=1 は株価のトレンドとしてある程度受け入れられる近似であり、ほぼエイリアシングを解消しているといえます。
T=0.5 〜 T=0.05 へとサンプリング周期を短くしても、株価のトレンドに殆ど変化は見られません。
故に、T=0.5 以下ではエイリアシングは起きず、良い近似と言えます。
Copyright 2004-2009 Atsufumi Ichinoseki. All rights reserved.
|

