絶対値を2つ含む不等式の問題と解き方
絶対値を含む方程式|X|=3はX=±3で、絶対値を外すと±がつくというのは、正しいです。しかし、絶対値を含む不等式 |X|>3の場合、この考え方をとると、|X|>3→X>±3→X>+3、X>-3となり、間違えてしまいます。正しくは以下のように、X<-3、3<Xです。
絶対値を含む不等式 |X|>3
絶対値を含む不等式の基本的な考え方は、絶対値の中がプラスの場合とマイナスの場合に分ける事です。
- X(絶対値の中)≧0の場合。|X|=Xだから、|X|>3はX>3となります。(付帯条件 X≧0)。連立不等式(X≧0、X>3)を解いて、答 X>3
- X(絶対値の中)<0の場合。|X|=-Xだから、|X|>3は-X>3。よってX<-3。(付帯条件 X<0)。連立不等式( X<0、X<-3)を解いて、答 X<-3
上記2つを合わせて、答はX<-3、3<X。
|X|>3をグラフで解く
|X|>3をグラフで考えると、Y=|X|のグラフがY=3のグラフより上にあるXの範囲が解になるので、下図のように、答は、X<-3、3<X、となります。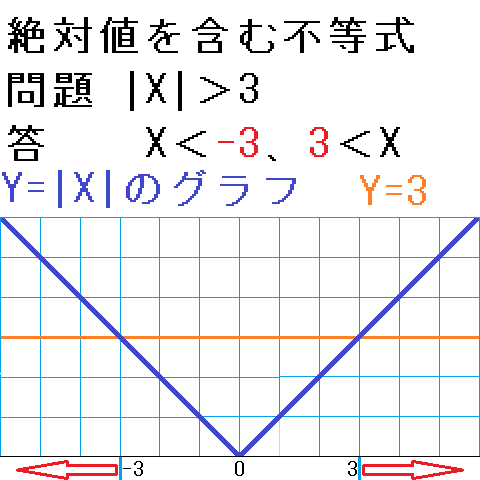
絶対値を含む不等式 |X-3|>5
問題 |X-3|>5。答 X-3>±5は間違いです。絶対値を外すと±がつくと、考えては、いけません。正しい考え方は、X-3がプラスの場合とマイナスの場合に分けて
- X-3がプラスの場合。|X-3|=X-3だから、問題はX-3>5となり、X>8。(付帯条件 X-3≧0、つまりX>3)連立不等式(X>3、X>8)を解いて、答 X>8
- X-3がマイナスの場合。|X-3|=-(X-3)だから、問題は-(X-3)>5となり、X<-2。(付帯条件 X-3<0、つまりX<3)連立不等式(X<3、X<-2)を解いて、答 X<-2
上記2つを合わせて、答はX<-2、8<X
絶対値を2つ含む不等式 |X-3|>|X|
問題 |X-3|>|X|。絶対値を外すと±がつくと、考えていると、±(X-3)>±X。これ解けますか。
「X-3」、「X」の正負はXの値が0と3で変化しますから、X<0、0≦X<3、3≦Xの三つの場合に分けます。最終的な解は、1の解or2の解or3の解です。
- (条件 X<0の場合)X-3<0だから、|X-3|=-(X-3)=-X+3。X<0だから。|X|=-X。よって、問題は-X+3>-Xとなります。これを解けば、+3>0という事になり、Xは全ての実数。(Xの値が何であっても成立する)ただし、条件があるので、答 X<0
- (条件 0≦X<3の場合)X-3<0だから、|X-3|=-(X-3)=-X+3。X≧0だから。|X|=X。よって、問題は-X+3>Xとなります。これを解けば、+3>2Xという事になり、X<3/2。連立不等式(0≦X<3、X<3/2)を解いて、答 0≦X<3/2
- (条件 3≦Xの場合)X-3>0だから、|X-3|=(X-3)。X≧0だから。|X|=X。よって、問題はX-3>Xとなります。これを解けば、-3>0という事になり、解なし。(この不等式を成立させるXの値は、ありません)
上記3つを合わせて答はX<3/2。
|X-3|>|X|をグラフで解く
Y=|X-3|のグラフがY=|X|のグラフより上になるのは、下図より、X<3/2。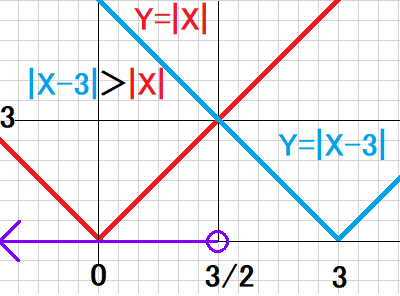
最後まで読んでいただいて、ありがとうございました。
