連立不等式の解き方と問題

連立不等式を解くとは、それぞれの不等式を解いて、共通部分を求める事です。数直線を書いて、重複する部分が解です。

連立不等式の４つのパターン

不等式が２つの場合、各不等式を解きます。例えば３X＋２＞５X＋６と５X－３＞３X＋７をそれぞれ解いて、X＜-2とX＞5となり、Xの単純な不等式が２つできます。

この２つの単純な不等式のうち、第一の不等式の＞の向きが左右２通り、第二の不等式の＞の向きも２通の可能性があるので、数直線の書き方は、４通り考えられます。

第一の不等式がX＞-2、第二がX＞5の場合
重複する部分＝解は５＜X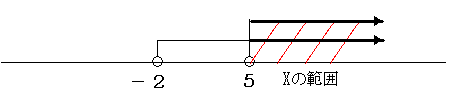
第一の不等式がX＞-2、第二がX＜5の場合
重複する部分＝解は－２＜X＜５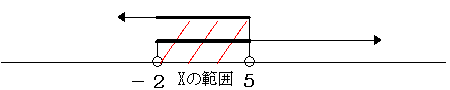
第一の不等式がX＜-2、第二がX＞5の場合
重複する部分はないので、解なし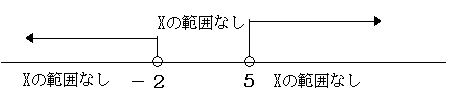
第一の不等式がX＜-2、第二がX＜5の場合
重複する部分＝解はX＜－２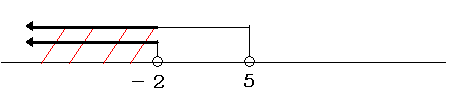

最後まで読んでいただいて、ありがとうございました。