六芒星の魔方陣の問題と解き方
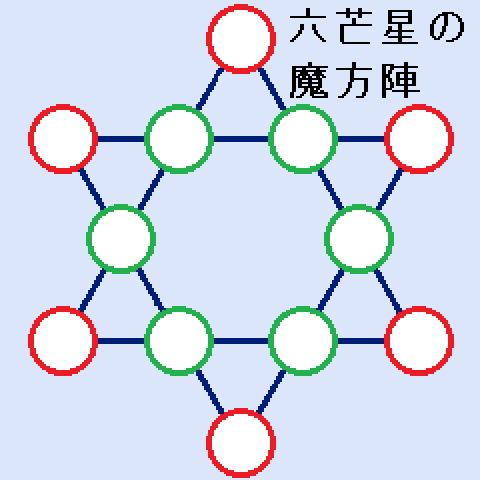 六芒星の魔方陣とは、六芒星の頂点と交点(全部で12か所)に1から12の整数を入れ、直線上の4個の数字の和Sが全て同じになるようにするものです。
六芒星の魔方陣とは、六芒星の頂点と交点(全部で12か所)に1から12の整数を入れ、直線上の4個の数字の和Sが全て同じになるようにするものです。
六芒星の魔方陣の問題(容易)
12か所のうち、6か所はすでに埋まっています。A~Fに入る数字を求めて下さい。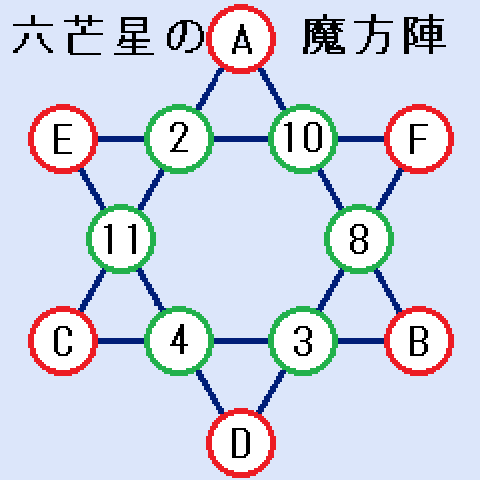
六芒星の魔方陣の解き方
3×3の魔方陣の1列が15になるのは、1~9の合計45を3で割って求められました。同じように、六芒星の魔方陣でも一列の和を求めます。
1列の和S=26
1~12の合計を求める公式もありますが、1~12の合計=1+2+3+4+5+6+7+8+9+10+11+12です。この級数の最初と最後、2番目と最後から2番目を組み合わせると13になりますが、その組み合わせは6組あります。よって、1~12の合計=13×6=78です。
1列の和Sを6列分足すと、それぞれの数字は2回ずつ足す事になります。6列の和=1~12の合計×2=78×2=156です。つまり、6S=156,S=26です。
連立方程式を解く
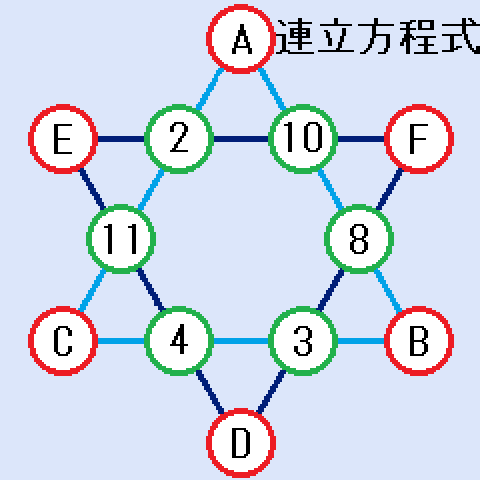 三角形ABCの辺について、和を考えると、以下の3つの式が得られます。
三角形ABCの辺について、和を考えると、以下の3つの式が得られます。
- A+10+8+B=26
- B+3+4+C=26
- C+11+2+A=26
式が3つ、変数が3つなので、容易に解けます。同様にDEFについても、容易に解けます。
解答は下図です。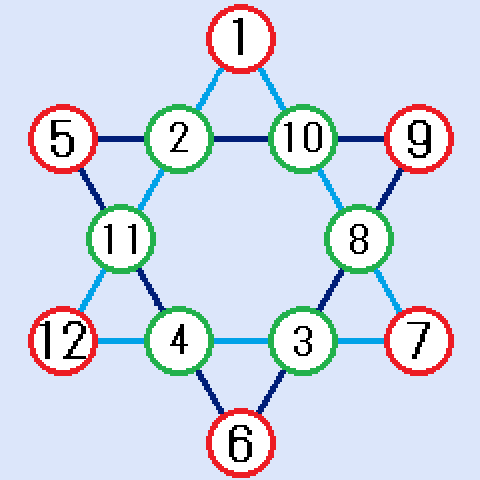
最後まで読んでいただいて、ありがとうございました。
