1から7の数字を入れる円魔法陣の解き方
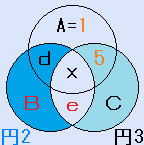
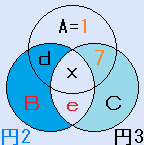
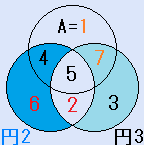
 円魔法陣とは、右の図のように、3つの円を重ねてできる7つの部分に1から7の数字を入れ、それぞれの円の中の4つの数字の和を等しくするものです。
円魔法陣とは、右の図のように、3つの円を重ねてできる7つの部分に1から7の数字を入れ、それぞれの円の中の4つの数字の和を等しくするものです。
円魔法陣のパズルは中学数学の教材にも使われています。教科書にも記載されています。
S=一つの円の中の4つの数字の和として、条件を式にすると、S=A+d+f+x。S=B+d+e+x。S=C+e+f+x。全ての数字の和=A+B+C+d+e+f+x=28となり、式が4つ変数が7つなので、単純に連立方程式を解いて、解を出す事は不可能です。
また、これらの方程式には、1≦A≦7などの条件が含まれていませんし、全ての数字は異なるという条件も含まれていません。
かなり面倒ですが、場合分けをして、解いていきます。
Aに入る数字は1から7ですが、A=1の場合でも、解は14種類あります。![]() A=1の場合の解は14種類
A=1の場合の解は14種類
A=1の場合の解き方
 まず、A=1として、fの値で、場合分けをします。
まず、A=1として、fの値で、場合分けをします。
『円1の中の4つの数字(A,d,x,f)と円2の中の4つの数字(B,d,x,e)の和は、等しい』が、この円魔法陣の条件です。
円1の中の4つの数字(A,d,x,f)と円2の中の4つの数字(B,d,x,e)を比べると、d,xが共通ですから、1+f=B+eとなります。
f=2の場合
f=2とすると1+f=B+eですから3=B+eですが、1,2がすでに使われているので、B+e=3となるB,eの数字の組み合わせはありません。
f=3の場合
f=3とすると1+f=B+eですから4=B+eですが、1,3がすでに使われているので、B+e=4となるB,eの数字の組み合わせはありません。
f=4の場合
f=4とすると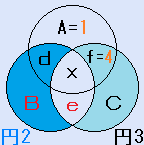 1+f=B+eですから、5=B+eとなります。B+e=5となる(B,e)の数字の組み合わせは、(2,3)か(3,2)です。
1+f=B+eですから、5=B+eとなります。B+e=5となる(B,e)の数字の組み合わせは、(2,3)か(3,2)です。
また、円2の中の4つの数字と円3の中の4つの数字を比べると、e,xが共通ですから、d+B=4+Cとなります。
f=4の場合、解は3種類あります。
- (B,e)=(2,3)の場合。
- d=5とすると、C=3となり、不適です。(3が重複)
- d=6とすると、C=4となり、不適です。(4が重複)
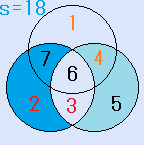
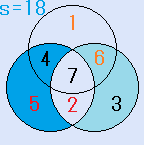
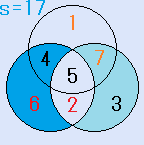
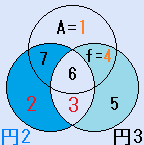 d=7とすると、C=5となり、残りのx=6で、これは、解です。一つの円の中の4つの数字の和S=18です。右図
d=7とすると、C=5となり、残りのx=6で、これは、解です。一つの円の中の4つの数字の和S=18です。右図
- (B,e)=(3,2)の場合。
- d=5とすると、C=4となり、不適です。(4が重複)
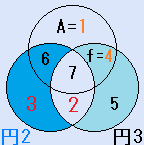 d=6とすると、C=5となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=18です。右図
d=6とすると、C=5となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=18です。右図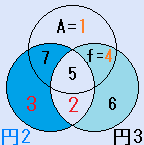 d=7とすると、C=6となり、残りのx=5で、これは、解です。一つの円の中の4つの数字の和S=17です。右図
d=7とすると、C=6となり、残りのx=5で、これは、解です。一つの円の中の4つの数字の和S=17です。右図
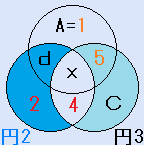
f=5の場合
 1+f=B+eですから、6=B+eとなります。B+e=6となる(B,e)の数字の組み合わせは、(2,4)か(4,2)です。
1+f=B+eですから、6=B+eとなります。B+e=6となる(B,e)の数字の組み合わせは、(2,4)か(4,2)です。
また、円2の中の4つの数字と円3の中の4つの数字を比べると、e,xが共通ですから、d+B=5+Cとなります。
f=5の場合、解は2種類あります。
 (B,e)=(2,4)の場合。
(B,e)=(2,4)の場合。
- d=3とすると、C=0となり、不適です。
- d=7とすると、C=4となり、不適です。(4が重複)
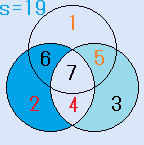
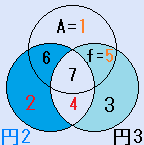 d=6とすると、C=3となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=19です。右図
d=6とすると、C=3となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=19です。右図
- (B,e)=(4,2)の場合。
- d=3とすると、C=2となり、不適です。(2が重複)
- d=6とすると、C=5となり、不適です。(5が重複)
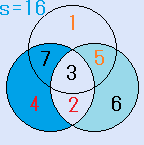
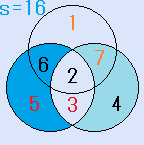
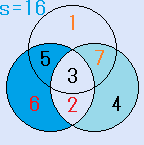
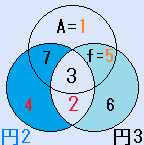 d=7とすると、C=6となり、残りのx=3で、これは、解です。一つの円の中の4つの数字の和S=16です。右図。
d=7とすると、C=6となり、残りのx=3で、これは、解です。一つの円の中の4つの数字の和S=16です。右図。
f=6の場合
 1+f=B+eですから、7=B+eとなります。B+e=7となる(B,e)の数字の組み合わせは、(2,5)か(3,4)か(4,3)か(5,2)です。
1+f=B+eですから、7=B+eとなります。B+e=7となる(B,e)の数字の組み合わせは、(2,5)か(3,4)か(4,3)か(5,2)です。
また、円2の中の4つの数字と円3の中の4つの数字を比べると、e,xが共通ですから、d+B=6+Cとなります。
f=6の場合、解は4種類あります。
- (B,e)=(2,5)の場合。
- d=3とすると、C=-1となり、不適です。
- d=4とすると、C=0となり、不適です。
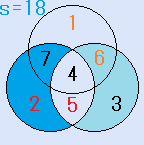
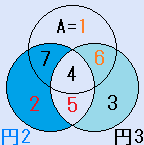 d=7とすると、C=3となり、残りのx=4で、これは、解です。一つの円の中の4つの数字の和S=18です。右図。
d=7とすると、C=3となり、残りのx=4で、これは、解です。一つの円の中の4つの数字の和S=18です。右図。
- (B,e)=(3,4)の場合。
- d=2とすると、C=-1となり、不適です。
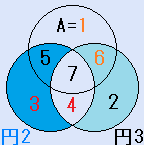 d=5とすると、C=2となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=19です。右図。
d=5とすると、C=2となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=19です。右図。- d=7とすると、C=4となり、不適です。(4が重複)
- (B,e)=(4,3)の場合。
- d=2とすると、C=0となり、不適です。
- d=5とすると、C=3となり、不適です。(3が重複)
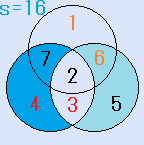
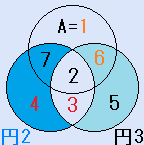 d=7とすると、C=5となり、残りのx=2で、これは、解です。一つの円の中の4つの数字の和S=16です。右図。
d=7とすると、C=5となり、残りのx=2で、これは、解です。一つの円の中の4つの数字の和S=16です。右図。
- (B,e)=(5,2)の場合。
- d=3とすると、C=2となり、不適です。(2が重複)
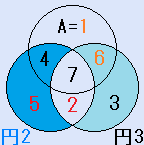 d=4とすると、C=3となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=18です。右図。
d=4とすると、C=3となり、残りのx=7で、これは、解です。一つの円の中の4つの数字の和S=18です。右図。- d=7とすると、C=6となり、不適です。(6が重複)
f=7の場合
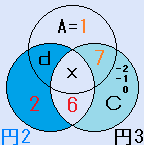
 1+f=B+eですから、8=B+eとなります。B+e=8となる(B,e)の数字の組み合わせは、(2,6)か(3,5)か(5,3)か(6,2)です。
1+f=B+eですから、8=B+eとなります。B+e=8となる(B,e)の数字の組み合わせは、(2,6)か(3,5)か(5,3)か(6,2)です。
また、円2の中の4つの数字と円3の中の4つの数字を比べると、e,xが共通ですから、d+B=7+Cとなります。
f=7の場合、解は5種類あります。
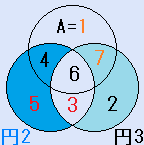
 (B,e)=(2,6)の場合。
(B,e)=(2,6)の場合。
- d=3とすると、C=-2となり、不適です。
- d=4とすると、C=-1となり、不適です。
- d=5とすると、C=0となり、不適です。
- (B,e)=(3,5)の場合。
- d=2とすると、C=-2となり、不適です。
- d=4とすると、C=0となり、不適です。
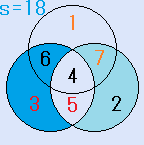
 d=6とすると、C=2となり、残りのx=4で、これは、解です。一つの円の中の4つの数字の和S=18です。
d=6とすると、C=2となり、残りのx=4で、これは、解です。一つの円の中の4つの数字の和S=18です。
- (B,e)=(5,3)の場合。
- d=2とすると、C=0となり、不適です。
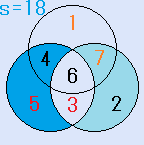
 d=4とすると、C=2となり、残りのx=6で、これは、解です。一つの円の中の4つの数字の和S=18です。
d=4とすると、C=2となり、残りのx=6で、これは、解です。一つの円の中の4つの数字の和S=18です。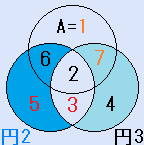 d=6とすると、C=4となり、残りのx=2で、これは、解です。一つの円の中の4つの数字の和S=16です。
d=6とすると、C=4となり、残りのx=2で、これは、解です。一つの円の中の4つの数字の和S=16です。
- (B,e)=(6,2)の場合。
- d=3とすると、C=2となり、不適です。(2が重複)
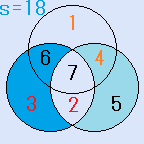
 d=4とすると、C=3となり、残りのx=5で、これは、解です。一つの円の中の4つの数字の和S=17です。
d=4とすると、C=3となり、残りのx=5で、これは、解です。一つの円の中の4つの数字の和S=17です。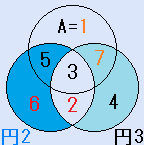 d=5とすると、C=4となり、残りのx=3で、これは、解です。一つの円の中の4つの数字の和S=16です。
d=5とすると、C=4となり、残りのx=3で、これは、解です。一つの円の中の4つの数字の和S=16です。
A=1の場合の解は14種類
一つの円の中の4つの数字の和Sの値が16,17,18,19の場合があり、円魔法陣の解は全部で14種類になります。
f=4の場合、解は3種類あります。

f=5の場合、解は2種類あります。
f=6の場合、解は4種類あります。

f=7の場合、解は5種類あります。
A=2,3,4,5,6の場合も解はある
A=1の場合の解では、 の青の部分に、2から6の数字が入っています。という事は、A=1の場合の14種類の解を右へ120度回転させれば、Aの部分に2から6の数字がくるので、A=2,3,4,5,6で解はあるということです。
の青の部分に、2から6の数字が入っています。という事は、A=1の場合の14種類の解を右へ120度回転させれば、Aの部分に2から6の数字がくるので、A=2,3,4,5,6で解はあるということです。
A=7の場合の解
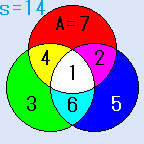 A=7の場合の解の例としては、右図のようなものがあります。
A=7の場合の解の例としては、右図のようなものがあります。
円魔法陣以外の魔方陣
魔方陣の問題には、円魔法陣以外に、![]() 五芒星と六芒星の魔方陣、三角形の各辺に3個の数字を入れる
五芒星と六芒星の魔方陣、三角形の各辺に3個の数字を入れる![]() 三角魔方陣などがあります。
三角魔方陣などがあります。
最後まで読んでいただいて、ありがとうございました。

