三角形の魔方陣の解き方(一辺に4個の数字)
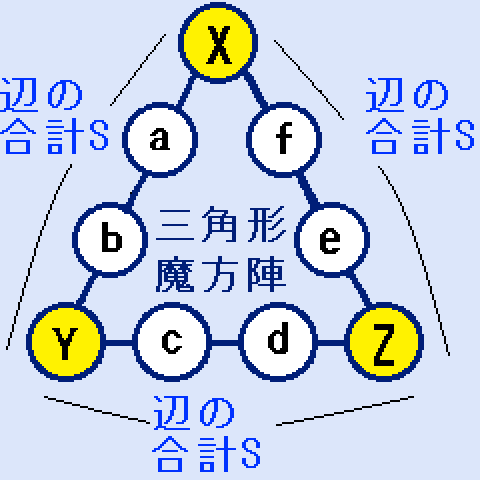 「1~9の数字を1回ずつ使って、三角形のどの辺の数字の和も等しくする」というパズルです。
「1~9の数字を1回ずつ使って、三角形のどの辺の数字の和も等しくする」というパズルです。
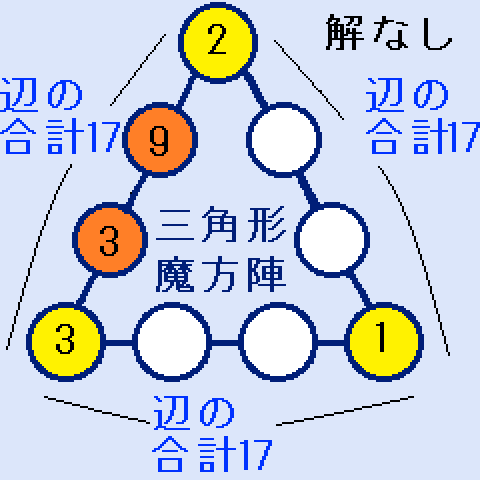
辺の合計S=17、18、19、20、21、22、23に限ります。うち、18と22の2つは解がありません。
理屈は、一辺に3個の数字を入れる三角魔方陣と変わりませんが、場合分けが多いので、手作業で全ての解を見つけるのは難しいです。![]() 三角形の魔方陣の解き方(一辺に3個の数字)
三角形の魔方陣の解き方(一辺に3個の数字)
辺の合計Sと頂点に入る数字の合計(X+Y+Z)の関係
上図のように、三角形の頂点に入る数字を(X,Y,Z)、辺の中に入る数字を(a,b,c,d,e,f)とします。
- 辺の合計S=X+a+b+Y
- 辺の合計S=Y+c+d+Z
- 辺の合計S=Z+e+f+X
上記3つの等式を辺々足すと(左辺同士、右辺同士を足す)、3S=2X+2Y+2Z+a+b+c+d+e+fとなります。
この式から、1~9の合計、45=X+Y+Z+a+b+c+d+e+fを辺々引くと、3S-45=X+Y+Z。
3をくくり出して、(S-15)×3=X+Y+Zとなります。…(1)
Sの値は17、18、19、20、21、22、23
Sの値が決まれば、(1)より、X+Y+Zの値が決まります。
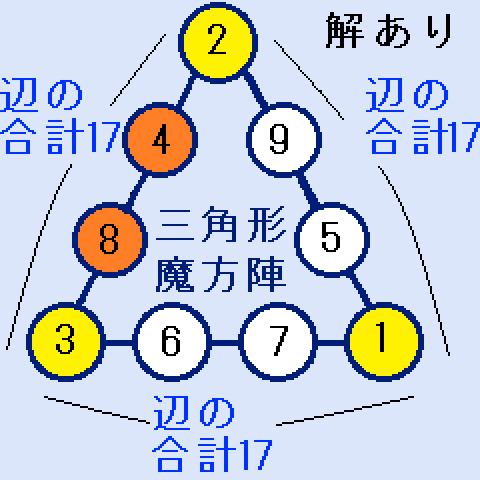
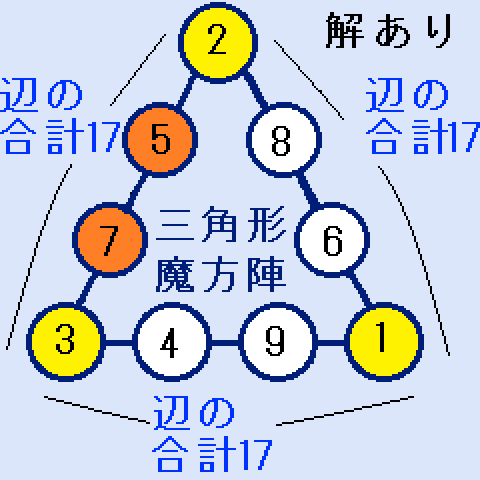 S=17すなわち、X+Y+Z=6の時。 (X,Y,Z)=(1,2,3)2つ解あり
S=17すなわち、X+Y+Z=6の時。 (X,Y,Z)=(1,2,3)2つ解あり- S=18すなわち、X+Y+Z=9の時。 (X,Y,Z)=(1,2,6),(1,3,5),(2,3,4)。解なし
- S=19すなわち、X+Y+Z=12の時。(X,Y,Z)=(1,2,9),(1,3,8),(1,4,7),(1,5,6),(2,3,7),(2,4,6),(3,4,5)解あり
- S=20すなわち、X+Y+Z=15の時。(X,Y,Z)=(1,5,9),(2,4,9),(2,5,8),(2,6,7),(3,4,8),(3,5,7),(4,5,6)解あり
- S=21すなわち、X+Y+Z=18の時。(X,Y,Z)=(1,8,9),(2,7,9),(3,6,9),(3,7,8),(4,5,9),(4,6,8),(5,6,7)解あり
- S=22すなわち、X+Y+Z=21の時。(X,Y,Z)=(4,8,9),(5,7,9),(6,7,8)解なし
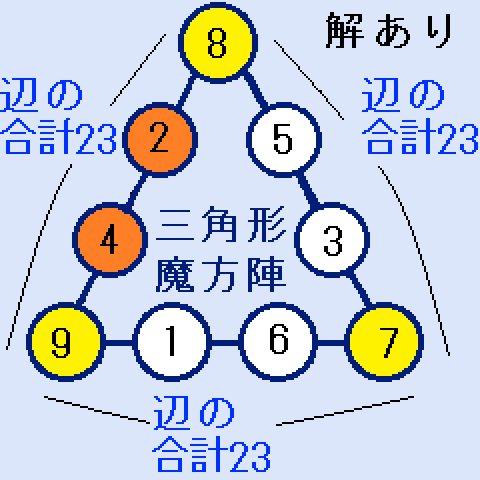 S=23すなわち、X+Y+Z=24の時。(X,Y,Z)=(7,8,9)1つ解あり
S=23すなわち、X+Y+Z=24の時。(X,Y,Z)=(7,8,9)1つ解あり
上記のうち、S=23、S=17、解のないS=18の場合の順に説明します。
S=23の時の解答(頂点の数字の合計=24)
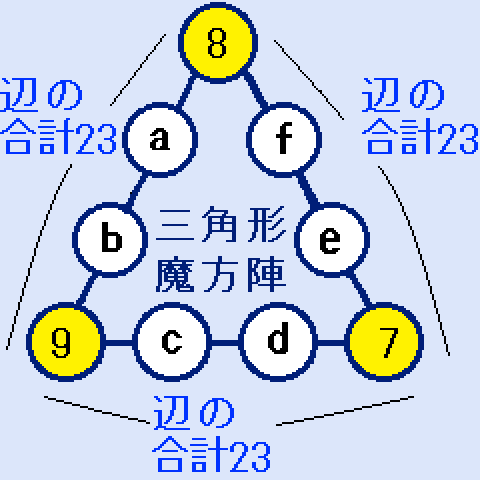 1~9の中から、3つの異なる数字を選んで、三角形の頂点の数字の合計=24になるのは、(7,8,9)だけです。右の図。a+b=6。c+d=7。e+f=8。となります。
1~9の中から、3つの異なる数字を選んで、三角形の頂点の数字の合計=24になるのは、(7,8,9)だけです。右の図。a+b=6。c+d=7。e+f=8。となります。重複を避けるために、a<b。c<d。e<f。とします。
S=23の時の解答は、左右の対称、回転、aとbの交換などを除くと、以下の 2例です。
7,8,9以外の最小の数字は1です。a=1とした場合から考えます。
解なし(a=1の場合)
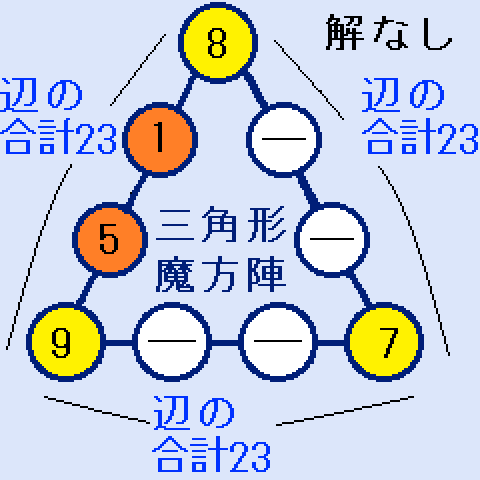 a=1とすると、b=5になります。ここで、cに入れる最小の数字は2です。
a=1とすると、b=5になります。ここで、cに入れる最小の数字は2です。- c=2の時、d=5となって、正解にはなりません。(5が重複)
- c=3の時、d=4になり、e=5、f=3となって、正解にはなりません。(3が重複)。
- c=4の時、d=3になり、e=5、f=3となって、正解にはなりません。(3が重複)。
- c=5の時、正解にはなりません。(5が重複)。
- c=6の時、d=1になり、正解にはなりません。(1が重複)
 c=1の時、d=6となって、e=3、f=5となります。正解の右図。
c=1の時、d=6となって、e=3、f=5となります。正解の右図。- c=3の時、d=4になり、正解にはなりません。(4が重複)
- c=4の時、正解にはなりません。(4が重複)
- c=5の時、d=2になり、正解にはなりません。(2が重複)
- c=6の時、d=1になり、e=3、f=5となります。これも解答ですが、重複を避けるc<dの仮定で除きます。
S=17の時の解答(頂点の数字の合計=6)
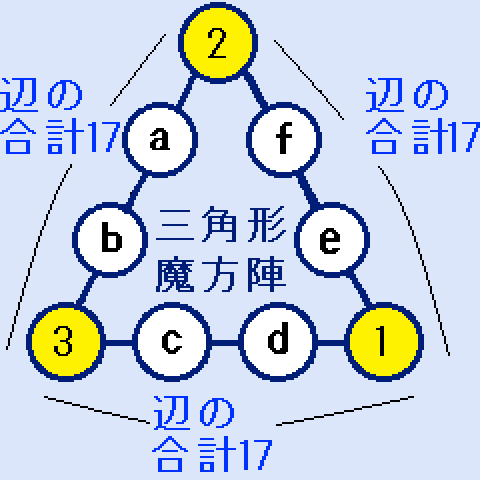 1~9の中から、3つの異なる数字を選んで、三角形の頂点の数字の合計=6になるのは、(1,2,3)だけです。右の図。a+b=12。c+d=13。e+f=14。となります。
1~9の中から、3つの異なる数字を選んで、三角形の頂点の数字の合計=6になるのは、(1,2,3)だけです。右の図。a+b=12。c+d=13。e+f=14。となります。重複を避けるために、a<b。c<d。e<f。とします。
S=17の時の解答は、左右の対称、回転、aとbの交換などを除くと、以下の2例です。
1,2,3以外の最小の数字は4です。a=4とした場合から考えます。
解答例1(a=4の場合)
 a=4とすると、b=8になります。ここで、cに入れる最小の数字は5です。
a=4とすると、b=8になります。ここで、cに入れる最小の数字は5です。- c=5の時、d=8となって、正解にはなりません。(8が重複)
- c=6の時、d=7になり、e=5、f=9となります。正解の右図。
- c=7の時、d=6になり、e=5、f=9となります。これも解答ですが、重複を避けるc<dの仮定で除きます。
- c=8の時、正解にはなりません。(8が重複)
- c=4の時、d=9となって、e=6、f=8となります。正解の右図。
- c=6の時、d=7になり、正解にはなりません。(7が重複)
- c=8の時、d=5になり、正解にはなりません。(5が重複)
- c=9の時、d=4になり、e=6、f=8となります。これも解答ですが、重複を避けるc<dの仮定で除きます。
S=18の時の解はない(頂点の数字の合計=9)
解がない事を示すには、膨大な場合分けが必要です。
1~9の中から、3つの異なる数字を選んで、頂点の数字の合計=9になる組み合わせは、(X,Y,Z):(1,2,6),(1,3,5),(2,3,4)の3通りがあります。大きく、この3つに場合分けします。
(X,Y,Z)=(1,2,6)の場合
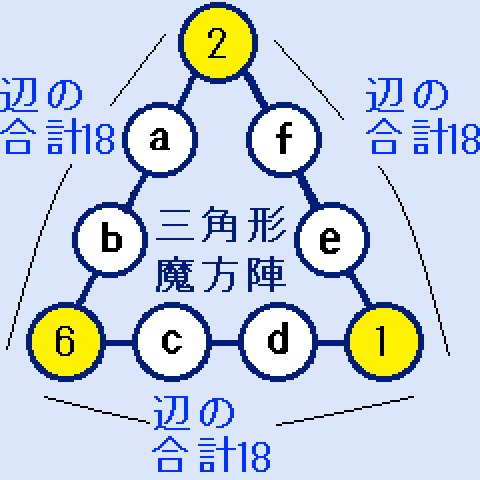 右の図。a+b=10。c+d=11。e+f=15。となります。解はありません。
右の図。a+b=10。c+d=11。e+f=15。となります。解はありません。(X,Y,Z)=(1,2,6)の場合 解なし
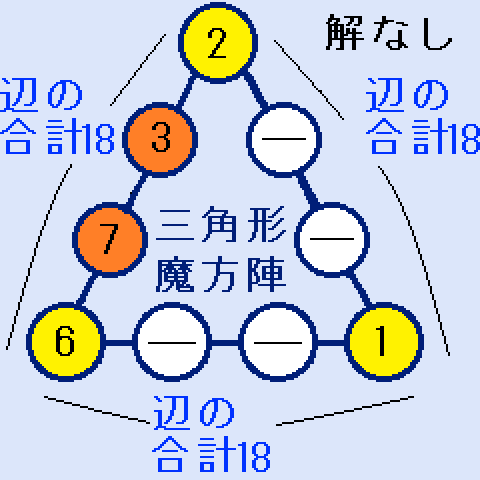 1,2,6以外の最小の数字は3です。
1,2,6以外の最小の数字は3です。a=3とすると、b=7になります。(右図)ここで、cに入れる最小の数字は4です。
- c=4の時、d=7となって、正解にはなりません。(7が重複)
- c=5の時、d=6になって、正解にはなりません。(6が重複)
- c=8の時、d=3になって、正解にはなりません。(3が重複)
- c=9の時、d=2になって、正解にはなりません。(2が重複)
(X,Y,Z)=(1,3,5)の場合
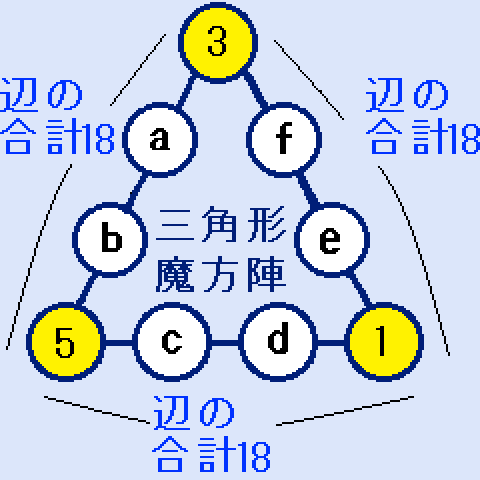 右の図。a+b=10。c+d=12。e+f=14。となります。解はありません。
右の図。a+b=10。c+d=12。e+f=14。となります。解はありません。(X,Y,Z)=(1,3,5)の場合 解なし
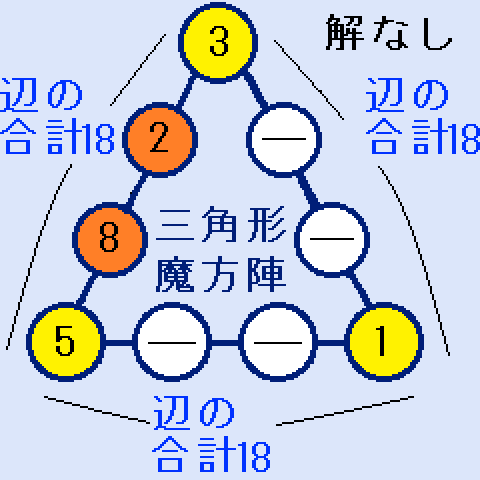 1,3,5以外の最小の数字は2です。
1,3,5以外の最小の数字は2です。a=2とすると、b=8になります。(右図)ここで、cに入れる最小の数字は4です。
- c=4の時、d=8となって、正解にはなりません。(8が重複)
- c=5の時、正解にはなりません。(5が重複)
- c=6の時、d=6となって、正解にはなりません。(6が重複)
- c=7の時、d=5となって、正解にはなりません。(5が重複)
- c=8の時、正解にはなりません。(8が重複)
- c=9の時、d=3になって、正解にはなりません。(3が重複)
a=3とすると、正解にはなりません。(3が重複)。
a=
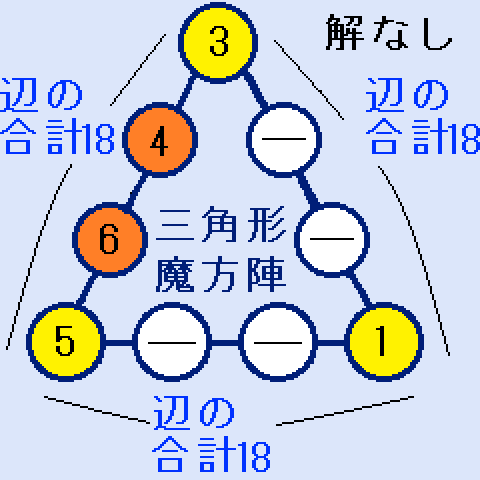 4とすると、b=6、になります。(右図)ここで、cに入れる最小の数字は2です。
4とすると、b=6、になります。(右図)ここで、cに入れる最小の数字は2です。- c=2の時、d=10となり、不適です。
- c=3の時、正解にはなりません。(3が重複)
- c=4の時、正解にはなりません。(4が重複)
- c=5の時、正解にはなりません。(5が重複)
- c=6の時、正解にはなりません。(6が重複)
- c=7の時、d=5になって、正解にはなりません。(5が重複)
- c=8の時、d=4になって、正解にはなりません。(4が重複)
- c=9の時、d=3になって、正解にはなりません。(3が重複)
(X,Y,Z)=(2,3,4)の場合
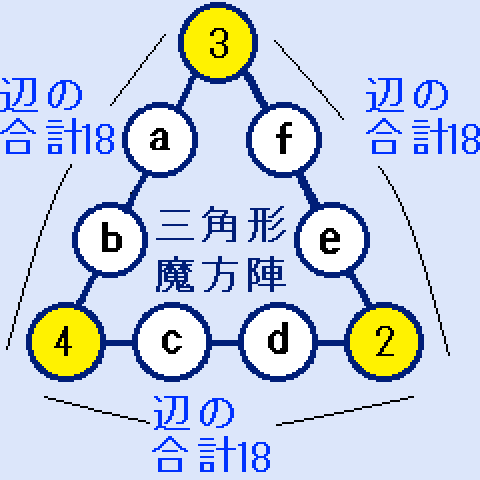 右の図。a+b=11。c+d=12。e+f=13。となります。解はありません。
右の図。a+b=11。c+d=12。e+f=13。となります。解はありません。(X,Y,Z)=(2,3,4)の場合 解なし
2,3,4以外の最小の数字は1です。
a=1とすると、b=10となり、不適です。
a=2とすると、正解にはなりません。(2が重複)
a=3とすると、正解にはなりません。(3が重複)
a=4とすると、正解にはなりません。(4が重複)
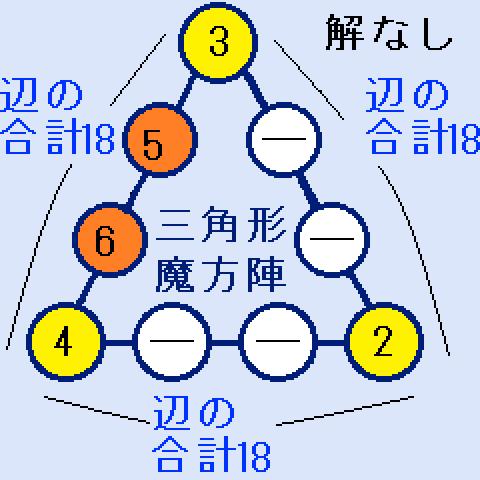 a=5とすると、b=6になります。ここで、cに入れる最小の数字は1です。
a=5とすると、b=6になります。ここで、cに入れる最小の数字は1です。- c=1の時、d=11となり、不適です。
- c=2の時、正解にはなりません。(2が重複)
- c=3の時、正解にはなりません。(3が重複)
- c=4の時、正解にはなりません。(4が重複)
- c=5の時、正解にはなりません。(5が重複)
- c=6の時、正解にはなりません。(6が重複)
- c=7の時、d=5になって、正解にはなりません。(5が重複)
- c=8の時、d=4になって、正解にはなりません。(4が重複)
- c=9の時、d=3になって、正解にはなりません。(3が重複)
a=6とすると、a=5にしたのと同じで、解はありません。
a=7とすると、b=4になり、正解にはなりません。(4が重複)
a=8とすると、b=3になり、正解にはなりません。(3が重複)
a=9とすると、b=2になり、正解にはなりません。(2が重複)
a=9とすると、b=2になります。ここで、cに入れる最小の数字は2です。
- c=1の時、d=11となり、不適です。
- c=2の時、d=10となって、正解にはなりません。
- c=3の時、d=9となって、正解にはなりません。(7が重複)
- c=4の時、d=8となって、正解にはなりません。(7が重複)
- c=5の時、d=7になって、正解にはなりません。(6が重複)
- c=6の時、d=6になって、正解にはなりません。(6が重複)
- c=7の時、d=5になって、正解にはなりません。(6が重複)
- c=8の時、d=4になって、正解にはなりません。(3が重複)
- c=9の時、d=3になって、正解にはなりません。(2が重複)
a=4とすると、b=6になって、正解にはなりません。(6が重複)
a=5とすると、b=5になって、正解にはなりません。(5が重複)
a=6とすると、正解にはなりません。(6が重複)
a=7とすると、b=3になって、a=3とした時と同じで、正解はありません。
a=8とすると、b=2になって、正解にはなりません。(2が重複)
a=9とすると、b=1になって、正解にはなりません。(1が重複)
解答例1(a=2の場合)
a=2とすると、b=4になります。ここで、cに入れる最小の数字は1です。
解なし(a=3の場合)
a=3とすると、b=3になり、正解にはなりません。(3が重複)
解答例1と同じ(a=4の場合)
a=4とすると、b=2、c=1、d=6、e=3、f=5となります。これも解答ですが、重複を避けるa<bの仮定で除きます。
解なし(a=5の場合)
a=5の場合は、a=1の場合と同じです。
解なし(a=6の場合)
a=6とすると、b=0になり、不適です。
解答例2(a=5の場合)
 a=5とすると、b=7になります。ここで、cに入れる最小の数字は4です。
a=5とすると、b=7になります。ここで、cに入れる最小の数字は4です。
解なし(a=6の場合)
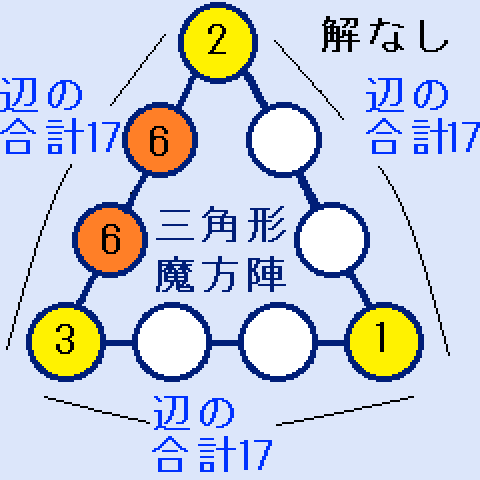 a=6とすると、b=6になり、正解にはなりません。(6が重複)
a=6とすると、b=6になり、正解にはなりません。(6が重複)
解答例3(a=7の場合)解答例2と同じ
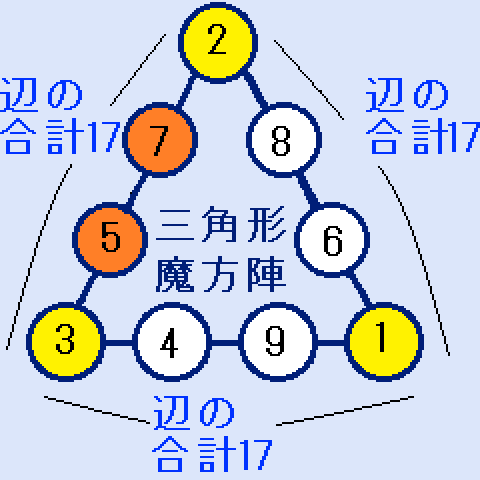 a=7とすると、b=5、c=4、d=9、e=6、f=8となります。これも解答ですが、重複を避けるa<bの仮定で除きます。
a=7とすると、b=5、c=4、d=9、e=6、f=8となります。これも解答ですが、重複を避けるa<bの仮定で除きます。
a=8の場合は、a=4の場合と同じです。
解なし(a=9の場合)
 a=9とすると、b=3になり、正解にはなりません。(3が重複)
a=9とすると、b=3になり、正解にはなりません。(3が重複)
最後まで読んでいただいて、ありがとうございました。
