三角形の魔方陣の解き方(一辺に３個の数字)

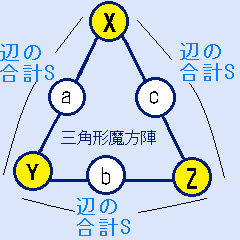三角形の魔方陣の問題「1～6の数字を１回ずつ使って、三角形のどの辺の数字の和も等しくする」というパズルです。

  1. 辺の合計S＝9の時、頂点の数字(X,Y,Z)は(1,2,3)。
  2. 辺の合計S＝10の時、頂点の数字(X,Y,Z)は(1,3,5)
  3. 辺の合計S＝11の時、頂点の数字(X,Y,Z)は(2,4,6)。
  4. 辺の合計S＝12の時、頂点の数字(X,Y,Z)は(4,5,6)となります。
  5. 辺の合計S≧13の時、解なしです。

三角形の魔方陣は3×3魔方陣より難しいです。

頂点の合計(X+Y+Z)と辺の合計Sの関係

頂点の数字の合計 (X+Y+Z)は、(辺の合計S-7)×3となります。小学生にも中学生にも説明するのは、難しいですが、

小学生レベルの説明

例えば、１つの辺の合計が9の時、３つの辺の合計は9×3=27。一方、６つの数字の合計は1+2+3+4+5+6=21。この差27-21=6は、頂点の数字を２回ずつ重複して数えるからです。つまり、頂点の数字の合計は6で、6=(辺の合計9-7)×3となります。

中学生レベルの説明

図のように、頂点に入る数字を(X,Y,Z)、辺の真ん中に入る数字を(a,b,c)とします。辺の合計S=X+a+Y=Y+b+Z=Z+c+Xです。

３つの等式（S=X+a+Y、S=Y+b+Z、S=Z+c+X）を辺々足すと(左辺同士、右辺同士を足す)、3S=2X+a+2Y+b+2Z+cとなります。この式から、1～6の合計、21=X+a+Y+b+Z+cを辺々引くと、3S-21=X+Y+Z。3をくくり出して、X+Y+Z=(辺の合計S-7)×3となります。…（１）

辺の合計Sが9の時、頂点は(1,2,3)だけ

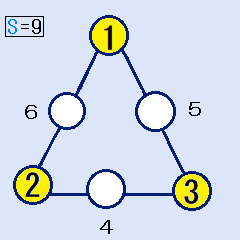三角形の魔方陣の頂点が(1,2,3)は解です（１）より、頂点の数字の合計＝(X+Y+Z)=(9-7)×3=6です。1～6の中から、３つの異なる数字を選んで、頂点の数字の合計=6になるのは、(1,2,3)だけです。右の図。

辺の合計が9ですから、白い丸の中の数字は、(6,4,5)に決まります。これは解です。

辺の合計Sが10の時、頂点は(1,3,5)だけ

（１）より、頂点の数字の合計＝(X+Y+Z)=(10-7)×3=9です。1～6の中から、３つの異なる数字を選んで、頂点の数字の合計=9になるのは、(1,2,6) (1,3,5) (2,3,4)だけです。これを過不足なく、数え上げるには次のように考えます。

  1. 1番小さい数字が1の時。
    (頂点の数字の合計は9だから)
    • 2番目に小さい数字が2→3つ目は6
    • 2番目に小さい数字が3→3つ目は5
    • 2番目に小さい数字が4→3つ目は x
    頂点の数字(X,Y,Z)は(1,2,6)か(1,3,5)
  2. 1番小さい数字が2の時。
    (頂点の数字の合計は9だから)
    • 2番目に小さい数字が3→3つ目は4
    • 2番目に小さい数字が4→3つ目は x
      • 頂点の数字(X,Y,Z)は(2,3,4)
  3. 1番小さい数字が3の時。
    (頂点の数字の合計は9だから)
    • 2番目に小さい数字が4→3つ目は x

頂点が(1,2,6)の場合

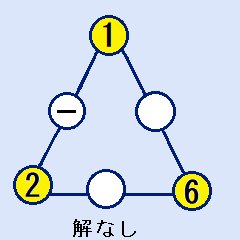三角形の魔方陣の頂点が(1,2,6)の場合は解なし辺の合計Sは10ですから、1と2の間に入れる数字はありません。これは解には、なれません。

頂点が(1,3,5)の場合

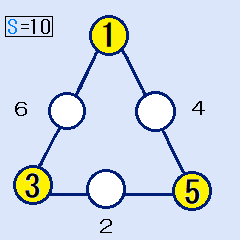三角形の魔方陣の頂点が(1,3,5)は解です辺の合計Sは10ですから、白い丸の中の数字は、(6,2,4)に決まります。これは解です。

頂点が(2,3,4)の場合

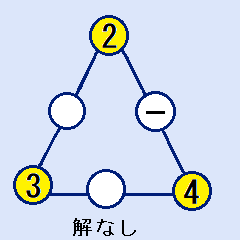三角形の魔方陣の三角形の頂点が(2,3,4)の場合は解なし辺の合計Sは10ですから、2と4の間に入れる数字はありません。これは解には、なれません。

辺の合計Sが11の時、頂点は(2,4,6)だけ

（１）より、頂点の数字の合計＝(X+Y+Z)=(11-7)×3=12です。1～6の中から、３つの異なる数字を選んで、頂点の数字の合計=12になるのは、(1,5,6) (2,4,6) (3,4,5)です。

過不足なく、数え上げるには上記の方法です。

頂点が(1,5,6)の場合

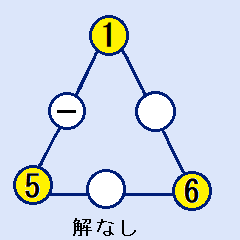三角形の魔方陣の頂点が(1,5,6)の場合は解なし辺の合計Sは11ですから、1と5の間に入れる数字はありません。これは解には、なれません。

頂点が(2,4,6)の場合

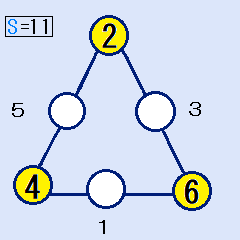三角形の魔方陣の頂点が(2,4,6)は解です辺の合計Sは11ですから、白い丸の中の数字は、(5,1,3)に決まります。これは解です。

頂点が(3,4,5)の場合

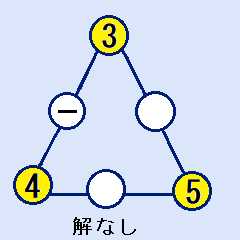三角形の魔方陣の三角形の頂点が((3,4,5)の場合は解なし辺の合計Sは11ですから、3と4の間に入れる数字はありません。これは解には、なれません。

辺の合計Sが12の時、頂点は(4,5,6)だけ

（１）より、頂点の数字の合計＝(X+Y+Z)=(12-7)×3=15です。1～6の中から、３つの異なる数字を選んで、頂点の数字の合計=15になるのは、(4,5,6)だけです。

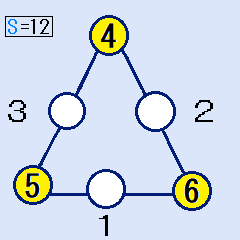三角形の魔方陣の頂点が(4,5,6)は解です辺の合計Sが12ですから、白い丸の中の数字は、(3,1,2)に決まります。これは解です。

魔法の三角形

ある教科書では、三角形の魔方陣のパズルを「魔法の三角形」という表現で紹介している。しかし、ここまで説明してきたように、これは、魔法ではなく、数学的に説明できるものである。

魔法陣と魔方陣の違い

魔法の三角形の魔方陣という表現は適切だろうか。

wikipediaでは、数学の「魔方陣」と魔術において使われる図形の「魔法陣」を区別して、別のページで説明している。数学の「魔方陣」では、3×3の魔方陣、4×4の魔方陣などを紹介していて、魔術において使われる図形の「魔法陣」では、水木しげるの『悪魔くん』に登場する魔法陣について説明している。

数学には魔法陣という表現はありませんが、魔方陣という表現はあります。また、「方」は四角形を意味するので、三角形の魔方陣という表現は間違いですが、この表現はWEB上では使われています。

最後まで読んでいただいて、ありがとうございました。