草加寺子屋 新学習プリント素因数分解パズル3

素因数分解パズルの例題

下の画像の４×４=16マスに1～9の数字を入れ、横行の４個の数字の積が、右の数字と一致し、縦列の４個の数字の積が、下の数字と一致するようにします。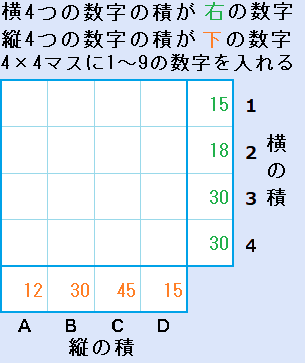

このパズルの仕組みを示す為の例題です。答を出す必要はありません。本当の問題は例題のあと、易しい問題が２つ、難しい問題が２つあります。

例題の答

例題の答のうちの１つが下図です。答は、これ以外にもあります。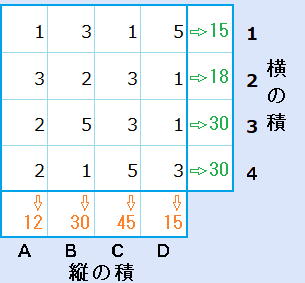

素因数分解パズルの問題１ 易しい

1が使えると、答が複数 出易くなります。なので、ここからの問題は、1を使わないというルールにします。素数に１を入れない理由と関係します。

素数は5年生で習います。素因数分解は中学1年生で習いますが、5年生でも理解できます。素因数分解とは、ある数を素数のかけ算で表す事です。

右と下にある「2357」などの数字は、210=2×3×5×7と素因数分解されるというヒントになっています。

問題１の答とヒント

この問題に対する答えは１つだけなので、易しい問題です。

問題１の答の緑の数字が確定する

縦Ｄ列の積=735=3×5×7×7と素因数分解されます。つまり、縦Ｄ列には7が２個入るという事です。しかし、横２行の積=24、横４行の積=225は７の倍数ではないので、Ｄ２,Ｄ４に7は入れません。よって、Ｄ１,Ｄ３に7が入る事になります。

縦Ｄ列の残りの数字は、3と5です。ここで、横２行の積=24は、５の倍数ではないので、5はＤ４に、3はＤ２に入ります。

縦Ｃ列の積=250=2×5×5×5と素因数分解されます。横２行の積=24は５の倍数ではないので、Ｃ２には2が入り、他の３マスには5が入ります。

縦Ａ列の積=36=2×2×3×3と素因数分解されます。横３行、横４行の積は奇数なので、2はＡ３,Ａ４に入れません。よって、Ａ１,Ａ２に2、Ａ３,Ａ４に3が入ります。

縦Ｂ列の４マスが残っていますが、横行の積を考えれば答に到達します。下図が答です。

素因数分解パズルの問題２ 易しい

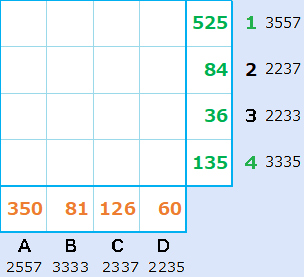
問題２の答とヒント

この問題に対する答えは１つだけです。

問題２の答の緑の数字が確定する

横１行の積=525=3×5×5×7と素因数分解されます。つまり、横１行には、5が２個入るという事です。しかし、縦Ｂ列、Ｃ列の積は５の倍数ではありません。よって、5はＡ１、Ｄ１に入る事になります。

縦Ｂ列の積=81=3×3×3×3ですから、縦Ｂ列の４個のマスは全て3になります。上記の事と合わせて、Ｃ１には7が入ります。

横４行の積=135は５の倍数ですから、横４行のどこかに5が入ります。しかし、Ｃ４、Ｄ４に5を入れると縦の積を合わせる事ができなくなるので、Ａ４に5が入る事になります。

問題２の答のオレンジの数字が確定する

横４行について考えます。すでに、5と3が入っているので、あと3が２個ですから、Ｃ４、Ｄ４に3が確定します。(1を使わないというルールです)

縦Ｄ列について考えます。すでに、5と3が入っているので、あと2が２個ですから、Ｄ２、Ｄ３に2が確定します。

問題２の答の赤の数字が確定する

横３行について考えます。すでに、2と3が入っているので、あと2と3が入ります。しかし、縦Ａ列の積=350は３の倍数ではないので、Ａ３には3は入れず、Ａ３に2が確定し、Ｃ３に3が確定します。

縦の積を考えれば、残り２マスは、7と2です。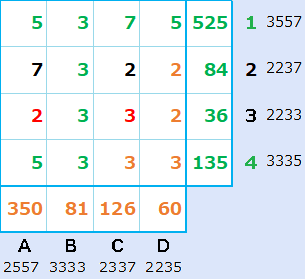

素因数分解パズルの問題３ 難しい

マスの中に入れる数字は2～9です。素数ではない4や6が入っても、かまいません。Ｂ３,Ｂ４,Ｃ３,Ｃ４は、最後にならないと決まりません。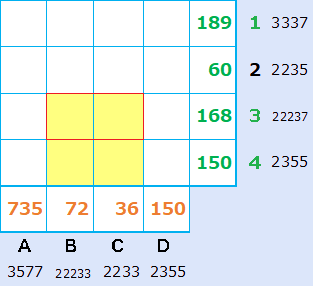

問題３の答とヒント

この問題に対する答えは２つあります。

問題３の答の緑の数字が確定する

横１行の積=189=3×3×3×7と素因数分解されます。つまり、横１行のどこかに、7があるという事です。しかし、縦Ｂ列、Ｃ列、Ｄ列の積は7の倍数ではないので、Ｂ１、Ｃ１、Ｄ１に7は入れません。よって、Ａ１に7が入る事になります。横１行に入る残りの数字は、３個の3ですから、Ｂ１、Ｃ１、Ｄ１の3が確定します。

横３行の積=168=2×2×2×3×7と素因数分解されます。上記と同じ理由で、Ａ３に7が入る事になります。

横４行の積=150=2×3×5×5と素因数分解されます。つまり、横４行には、5が２個入るという事です。しかし、縦Ｂ列、Ｃ列の積は５の倍数ではないので、Ｂ４、Ｃ４に5は入れません。よって、Ａ４、Ｄ４に5が入る事になります。

縦Ｄ列について考えます。すでに、5と3が入っているので、残りは2と5です。横３行の積=168は５の倍数ではないので、Ｄ２に5、Ｄ３に2が確定します。

問題３の答のオレンジの数字が確定する

横２行について考えます。残りの数字は2と2と3です。縦Ａ列の積は奇数なので、Ａ２に2は入れません。よって、Ａ２に3、Ｂ２、Ｃ２に2が入る事になります。

ここで、残ったマスは、Ｂ３、Ｃ３、Ｂ４、Ｃ４です。

Ｂ３、Ｃ３をかけると、１６８÷７÷２＝１２になるので、
Ｂ３、Ｃ３は、3と4か2と6です。

問題３の答 その1

Ｂ３、Ｃ３が、3と4の場合。

Ｃ３に4が入ると、縦Ｃ列の積が36になれないので、4はＢ３に、3はＣ３に入ります。Ｂ４とＣ４は、縦の積を考えれば決まります。下図が答になります。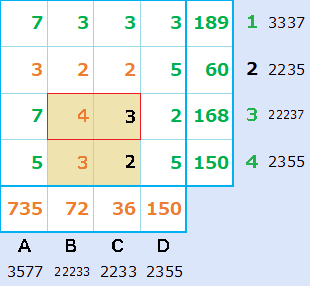

問題３の答 その2

Ｂ３、Ｃ３が、2と6の場合。

Ｃ３に6が入ると、Ｃ４に1が入り、マスの中に入れる数字は2～9というルールに反するので、6はＢ３に、2はＣ３に入り、下図が答になります。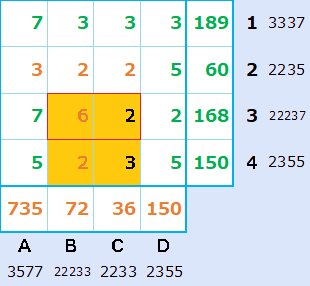

素因数分解パズルの問題４ 難しい

Ａ１,Ｄ１に入る数字が２通りあるので、途中、場合分けをします。さらに、場合分けをする事もあります。よって、難しい問題です。結局、答が３つ出ます。

考え方も複数あります。以下の説明は、そのうちの１つです。１通りに決まるマスから考えます。

問題４の答の緑の数字が確定する

縦Ｂ列の積=54=2×3×3×3と素因数分解されます。横３行、横４行の積は奇数なので、Ｂ３,Ｂ４に2は入れません。Ｂ３,Ｂ４には、3が入る事になります。

縦Ｃ列の積=60=2×2×3×5と素因数分解されます。横３行、横４行の積は奇数なので、Ｃ３,Ｃ４に2は入れません。２つの2は、Ｃ１,Ｃ２に入る事になります。

ここで、横２行を考えます。横２行で残っている数字は、2と2と3です。また、縦Ａ列の積は奇数です。よって、Ａ２に2は入れないので、3が入ります。

横２行で残っている数字は、2と2になりました。空きマスは、Ｂ２,Ｄ２ですから、そこに2が入ります。

縦Ｂ列を見ると、空きマスはＢ１だけなので、そこに3が入ります。

縦Ａ列を考えます。縦Ａ列の残りの数は、5と5と7です。横４行の積=225は7の倍数ではないので。Ａ４に7は入れず、5が入ります。

ここで、横１行の残りの空きマスについて考えると、Ａ１,Ｄ１は、5,7か7,5です。

Ａ１,Ｄ１が5,7の場合

Ａ１,Ｄ１に、5、7と入れると、縦Ａ列の唯一の空きマスに7が入ります。全体を見渡すと、残りの空きマスは、右下隅のＣ３,Ｄ３,Ｃ４,Ｄ４です。

横３行を見ると、Ｃ３に入れるのは、3と5なので、場合分けをします。

Ｃ３が3の場合

まず、Ｃ３が3の場合は、Ｄ３が5に、Ｃ４が5、Ｄ４が3になります。下図が答になります。

Ｃ３が5の場合

Ｃ３が5の場合は、3と5を入れ替えた答になります(下図)。

Ａ１,Ｄ１が7,5の場合

Ａ１,Ｄ１に、7、5と入れると、縦Ａ列の唯一の空きマスに5が入ります。残りの空きマスは、右下隅のＣ３,Ｄ３,Ｃ４,Ｄ４です。

横３行を見ると、Ｃ３に入るのは、3か7ですしかし、縦Ｃ列の積=60は7の倍数ではないので、7は入れず、3が入ります。残りの空き３マスに7,5,3を入れて、下図が答になります。

最後まで読んでいただいて、ありがとうございました。