二次関数の最小値と最大値

二次関数 Y＝F（X）＝X２－２aX＋a２－1の最小値と最大値を求めよ。
ただし、１＜＝x＜＝５とする。
平方完成するとX２－２aX＋a２－1＝（X－a）２－１となり、
頂点のx座標＝aとなります。 平方完成の公式を丸暗記してはダメ
この頂点とx＝１、x＝３（１と５の中点）、x＝５の位置関係によって場合分けします。

二次関数の最小値

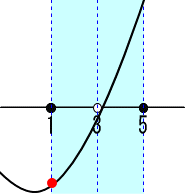  1. 二次関数の最小値１ 頂点のx座標aが　a＜＝１の場合。
    X＝１の時、最小値＝F（１）
    ＝１２－２a１＋a２－1
    ＝a２－２a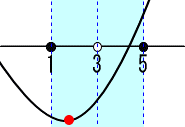
  2. 二次関数の最小値２ 頂点のx座標aが　１＜a＜＝３の場合。
    X＝aの時、最小値＝F（a）＝－１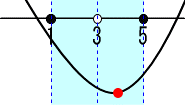
  3. 二次関数の最小値３ 頂点のx座標aが　３＜a＜＝５の場合。
    X＝aの時、最小値＝F（a）＝－１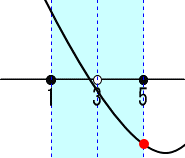
  4. 二次関数の最小値４ 頂点のx座標aが　５＜aの場合。
    X＝５の時、最小値＝F（５）
    ＝５２－２a５＋a２－1
    ＝a２－１０a＋２４

二次関数の最大値

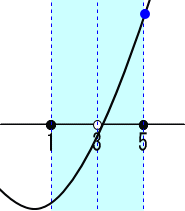  1. 二次関数の最大値１ 頂点のx座標aが　a＜＝１の場合。
    X＝５の時、最大値＝F（５）
    ＝５２－２a５＋a２－1
    ＝a２－１０a＋２４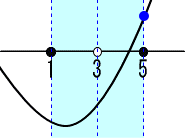
  2. 二次関数の最大値２ 頂点のx座標aが　１＜a＜＝３の場合。
    X＝５の時、最大値＝F（５）
    ＝５２－２a５＋a２－1
    ＝a２－１０a＋２４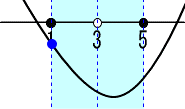
  3. 二次関数の最大値３ 頂点のx座標aが　３＜a＜＝５の場合。
    X＝１の時、最大値＝F（１）
    ＝１２－２a１＋a２－1
    ＝a２－２a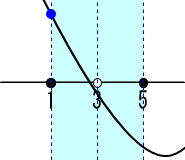
  4. 二次関数の最大値４ 頂点のx座標aが　５＜aの場合。
    X＝１の時、最大値＝F（１）
    ＝１２－２a１＋a２－1
    ＝a２－２a

最後まで読んでいただいて、ありがとうございました。