コンパスだけで正方形の4頂点を決める
コンパスの針は紙に穴を開けないものとします。円弧と円弧の交点に針を置く事は許されます。定規は使いません。
問題自体は非常にシンプルなので、簡単そうに見えます。
ヒント、辺の長さの比が3:4:5の三角形は直角三角形で、3と4の最小公倍数は12です。
コンパスだけで、正方形の4頂点を決める方法の答
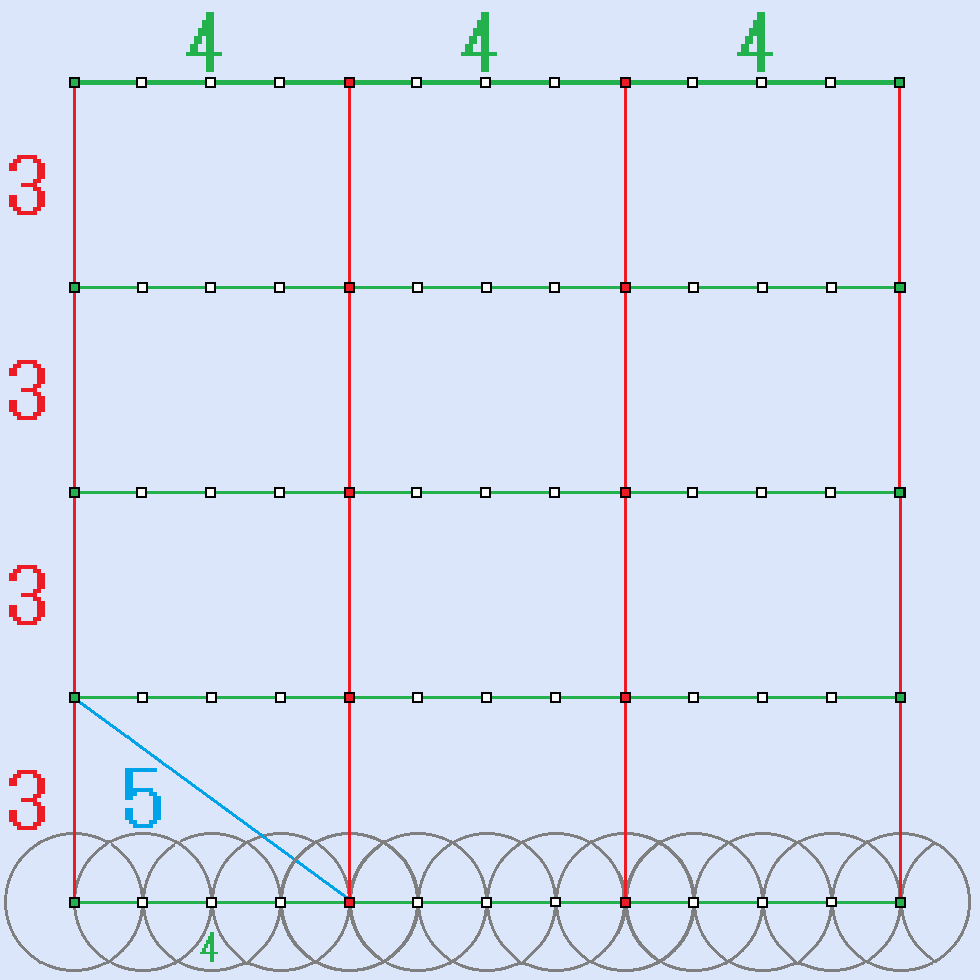 以下、この正方形の4頂点を決める方法の作図方法を説明します。
以下、この正方形の4頂点を決める方法の作図方法を説明します。
まず等間隔の目盛りを作成
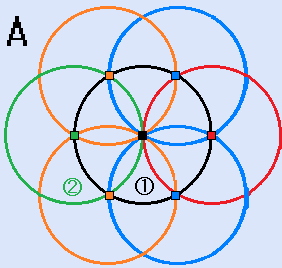
- ①の円を書きます。
- 上記の円の円周上の任意の点を中心に同じ半径で②の円を書きます。
- ①の円と②の円の2か所の交点を中心として、それぞれ同じ半径で、2つの円を書きます。
- 上記の2つの円と①の円の交点を中心として、それぞれ同じ半径で、2つの円を書きます。(上の図A)
- 上記の方法を右の方へ続けて作成したのが、下の図Bです。
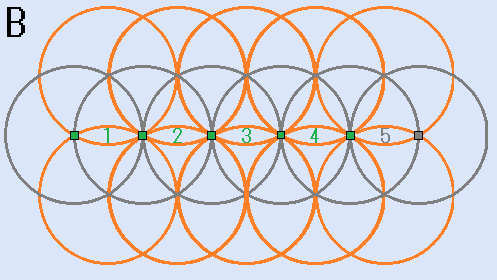
等間隔の目盛り(1から5)ができました。
辺の長さの比が3:4:5の三角形を作る
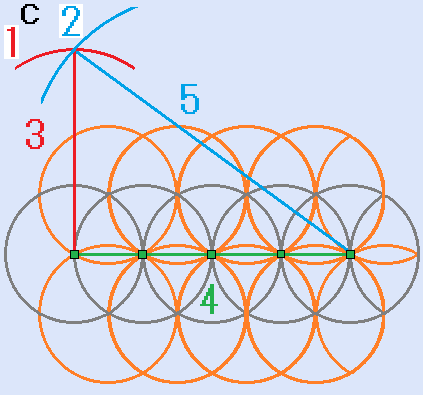
- 上記Bの一番左の目盛りの点を中心として、半径3(目盛り)の円弧を描きます。
- 上記Bの左から5番目の目盛りの点を中心として、半径5(目盛り)の円弧を描きます。
- 目盛りの左右の端の点、2つの円弧の交点は、3:4:5の三角形の頂点です。(図C)
辺の長さの比が3:4の長方形を作る
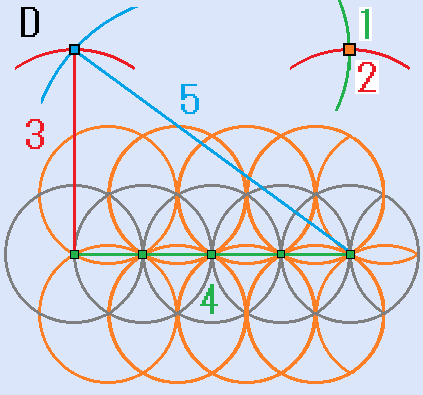
- 上記の円弧の交点を中心として、半径4(目盛り)の円弧を描きます。
- 左から5番目の目盛りの点を中心として、半径3(目盛り)の円弧を描きます。
- 上記の2つの円弧の交点と前記の3:4:5の三角形の頂点は、辺の長さの比が3:4の長方形の頂点です。(図D)
図Dを右と上に拡張する
- 目盛りの部分を右の方へ続けて作成します。
- 左から5番目の目盛りの点を中心として、半径5(目盛り)の円弧を描きます。
- 左から9番目の目盛りの点を中心として、半径3(目盛り)の円弧を描きます。
- 図Dで作った長方形の右上の頂点を中心として、半径5(目盛り)の円弧を描きます。
- 図Dで作った長方形の左上の頂点を中心として、半径3(目盛り)の円弧を描きます。
- 4と5の交点を中心として、半径4(目盛り)の円弧を描きます。
- 図Dで作った長方形の右上の頂点を中心として、半径3(目盛り)の円弧を描きます。
下のE図ができます。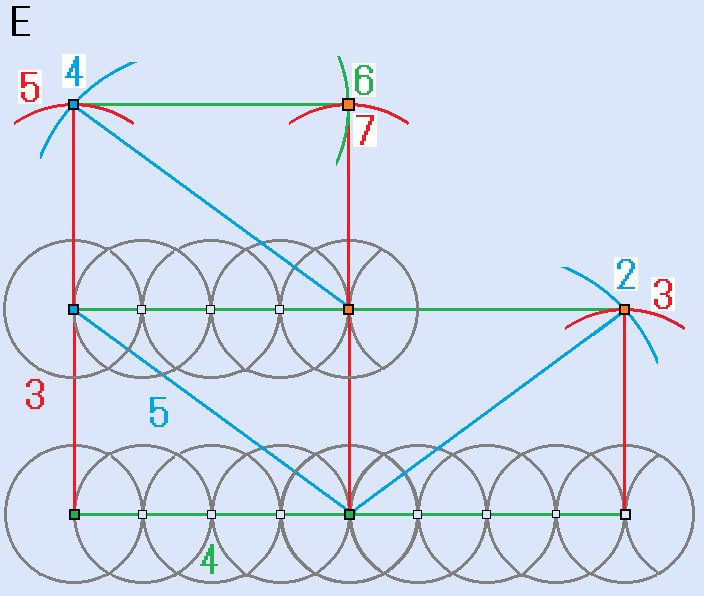
3と4の最小公倍数は12
E図から、さらに上へ2回、右へ1回拡張すれば、正方形の4点がコンパスだけで作図できます。(縦3目盛り×4、横4目盛り×3の正方形)
最後まで読んでいただいて、ありがとうございました。
