三次方程式 因数分解による解き方と多項式の除法
因数定理→三次方程式の因数分解が教科書の順番ですが、三次方程式の解き方から始めた方が理解し易いと思います。
重要なのは、多項式の除法です。組立除法より簡単です。組立除法は、いりません。以下の![]() 多項式の除法だけを見ればいいかもしれません。
多項式の除法だけを見ればいいかもしれません。
三次方程式の因数分解による解き方
三次方程式を解くとは、因数分解して、(X-A)(X-B)(X-C) = 0 とする事です。この時、三次方程式の解はX=A, B, Cとなります。
三次方程式の練習問題
三次方程式X3−6X2+11X−6=0の解は?
左辺を因数分解すると、(X−1)(X−2)(X−3)=0ですから、解はX=1,2,3です。
左辺を因数分解するには、どうしたら良いかは、追々、説明します。
解の求め方
練習問題の解、1,2,3をどうしたら求められるでしょうか。
f(X)=X3−6X2+11X−6=(X−1)(X−2)(X−3)とすると、
- f(1)=(1−1)×(1−2)×(1−3)=0
- f(2)=(2−1)×(2−2)×(2−3)=0
- f(3)=(3−1)×(3−2)×(3−3)=0
これが、なんとなくの因数定理です。少し正確に言うと、f(a)=0ならば、f(X)は、(X-a)を因数に持つというのが因数定理です。(当たり前だけど)
解の候補
(X-A)(X-B)(X-C)を展開するとX3…−ABCですが、練習問題の場合は、(X−1)(X−2)(X−3)を展開すると、X3・・・−6となります。
−ABCが−6だから、A、B、Cの候補は定数項ABCの約数。つまり、かけて、−6になる数です。
よって、解の候補は+1、+2、+3、+6、−1、−2、−3、−6です。
f(1)、f(2)、f(3)、f(6)、f(−1)、f(−2)、f(−3)、f(−6)を計算すると、f(X)=0となるのはX=1、2、3の時で、解はX=1,2,3です。
ただ、f(1)からf(−6)までを全て計算するのは面倒です。実は、1つだけで計算すれば良いのですが。
三次方程式の解き方・教科書の解法
解の候補を1つだけ求めます。
計算が簡単なf(1)を求めると、f(1)=0となる事が分かります。
因数定理よりf(X)は(X−1)で割り切れて、X3−6X2+11X−6=(X−1)(X2+□X+△)となるはずです。
多項式の除法で(X2+□X+△)を求めます。
(X2+□X+△)=(X3−6X2+11X−6)÷(X−1)=X2−5X+6になって、X3−6X2+11X−6=(X−1)X2−5X+6となります。
ここで問題なのは、X2−5X+6の求め方ですが、これは以下の多項式の除法で行ないます。
次数が3次方程式から2次方程式に下がった(バンザーイ)。
(X2−5X+6)を因数分解する。(かけて+6、足して−5になるのは、−2と−3)
(X2−5X+6)=(X−2)(X−3)
よって、X3−6X2+11X−6=(X−1)(X−2)(X−3)。解はX=1,2,3です。
因数分解できない時は、解の公式を使う。あるいは、![]() 因数分解たすき掛けを使わない方法 応用
因数分解たすき掛けを使わない方法 応用
多項式の除法
- 多項式の除法は、整数の割り算と同じような方法で行います。組立除法より簡単です。
- マイナスを引くとプラスになる事に注意。
多項式の除法 筆算
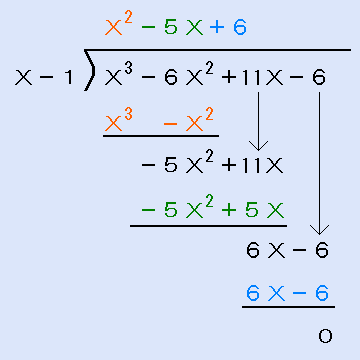
- X3−6X2+11X−6の先頭X3とX−1の先頭Xだけを見てX2を立てます。X2とX−1をかけて、X3−X2。引き算してから、+11Xを下ろします。
- −5X2+11Xの先頭−5X2とX−1の先頭Xだけを見て−5Xを立てます。 −5XとX−1をかけて、−5X2+5X。引き算してから、−6を下ろします。
- 6X−6の先頭6XとX−1の先頭Xだけを見て6を立てます。6とX−1をかけて、6X−6。引き算して0、割り切れました。
ややこしい感じがしますが、先頭だけを見るという事に注意すれば、小学校の割り算と同じです。組立除法より簡単な理由がここにあります。
整数の割り算 筆算
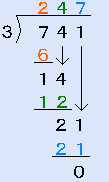 これは、小学生のレベルですから、以下の説明を見る必要はないでしょう。前の多項式の除法との関係で書きました。
これは、小学生のレベルですから、以下の説明を見る必要はないでしょう。前の多項式の除法との関係で書きました。
- 7と3を見て、2を立てます。2と3をかけて、6。引き算し4を下ろします。
- 14と3を見て、4を立てます。4と3をかけて、12。引き算し1を下ろします。
- 21と3を見て、7を立てます。7と3をかけて21。引き算し0。
最後まで読んでいただいて、ありがとうございました。
