集合のかつ,またはの記号の覚え方は簡単

U￣はカップに見えるでしょ。∪はカップ(cup)と読みます。意味は「または」です。カップのふちにある集合Ａと集合Ｂの要素が、全部カップの中に落ちた、と覚えます。下の図。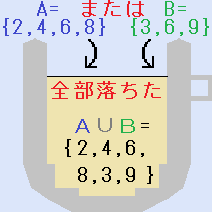Ａ∪Ｂが集合Ａ、集合Ｂの全部の要素を表すことの説明図。

  • 集合Ａ＝｛２，４，６，８｝ (2の倍数)
  • 集合Ｂ＝｛３，６，９｝ (3の倍数)とする時
  • Ａ∪Ｂ＝｛２，４，６，８，３，９｝
  • Ａ∩Ｂ＝｛６｝(6の倍数)です。

＿∩は帽子に見えるでしょ。∩はキャップ(cap)と読みます。意味は「かつ」です。∪カップを全部と覚えれば、∩キャップを一部と覚えるのは簡単です。

集合の記号∪と∩の覚え方,こじつけ

  1. ∪も、全部も、プラスのイメージです。
  2. ∩も、一部も、マイナスのイメージです。

こじつけは以下のようになります。

∪はプラスのイメージ

  1. 両手を上げて、∪の字を作ってください。（プラスのイメージ）
  2. 両手を下げて、∩の字を作ってください。（マイナスのイメージ）

全部はプラスのイメージ

  1. 全部。（プラスのイメージ）
  2. 一部。（マイナスのイメージ）

Ａ∪Ｂは全部(和集合、または)

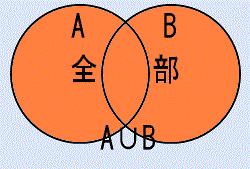Ａ∪Ｂのベン図、Ａ∪Ｂは全部を表す。∪は両手を上に広げたプラスのイメージですから、Ａ∪ＢはＡ、Ｂの全部です。ＡまたはＢという意味になります。A∪B＝｛ x｜x∈A または x∈B ｝。ベン図で表せば、右の図のようになります。

Ａ∩Ｂは一部(積集合、かつ)

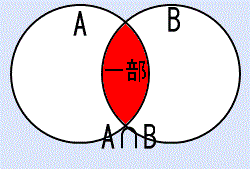Ａ∩Ｂのベン図、Ａ∩Ｂは一部を表す。∩は両手を下に広げたマイナスのイメージですから、Ａ∩ＢはＡ、Ｂの一部です。ＡかつＢという意味になります。A∩B＝｛ x｜x∈A かつ x∈B ｝。ベン図で表せば、右の図のようになります。

(A∪B)のバーと(Aのバー)∪(Bのバー)練習問題

集合のかつ,またはの記号の意味を覚えたところで、練習問題です。

  • 全体集合U＝｛１，２，３，４，５，６，７，８，９｝
  • 部分集合Ａ＝｛２，４，６，８｝　（２の倍数）
  • 部分集合Ｂ＝｛３，６，９｝　（３の倍数）

    上記の条件で以下の２つの集合の要素を求めよ。（｛　，　，　｝の表現で）

  1. Ａ∪Ｂ　（(Ａ∪Ｂ)のバー）
  2. Ａ∪Ｂ　(Ａのバー)∪(Ｂのバー)

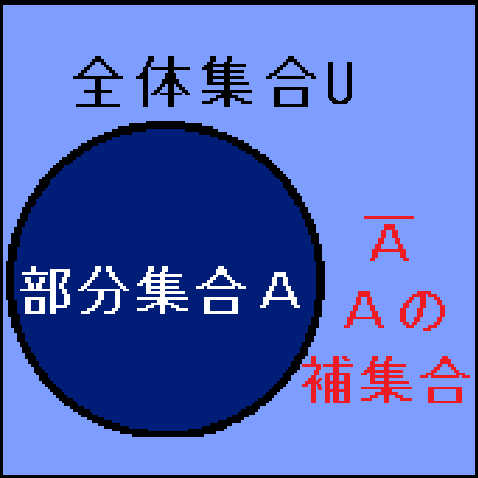全体集合Ｕと部分集合ＡとＡの補集合の関係を表す図ＡをＡのバーと読み、Ａの補集合を意味します。全体集合(Universal Set)は、頭文字のUで表すのが一般的です。集合の記号カップ∪とは全くの別物です。

  1. (Ａ∪Ｂ)のバーの答

    Ａ∪Ｂ＝ＡとＢの全部＝｛２，３，４，６，８，９｝。
    バーをつけて、(Ａ∪Ｂ)のバー：Ａ∪Ｂ＝｛１，５，７｝

  2. (Ａのバー)∪(Ｂのバー)の答

    Ａのバー：Ａ＝｛１，３，５，７，９｝（奇数）
    Ｂのバー：Ｂ＝｛１，２，４，５，７，８｝（３の倍数でない）
    (Ａのバー)∪(Ｂのバー)：Ａ∪Ｂ＝｛１，３，５，７，９｝と｛１，２，４，５，７，８｝の全部＝｛１，２，３，４，５，７，８，９｝

ド・モルガンの法則の覚え方

Ａ∪Ｂ＝Ａ∩Ｂ。Ａ∩Ｂ＝Ａ∪Ｂというド・モルガンの法則があります。よーく見れば、覚え方は簡単です。バーのイメージは反対ですから、∪と∩がひっくり返るというこじつけです。

最後まで読んでいただいて、ありがとうございました。