sin cos tanの表の覚え方は不要
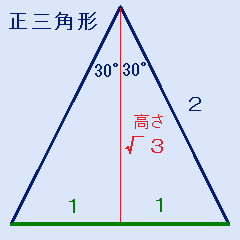 sin cos tanの表を覚えるより、30°,60°,90°の三角形の辺の比が、1:2:ルート3になる事の方が重要。1:2:√3から、sin cos tanの表が出てくるからです。次のlinkを見て下さい。
sin cos tanの表を覚えるより、30°,60°,90°の三角形の辺の比が、1:2:ルート3になる事の方が重要。1:2:√3から、sin cos tanの表が出てくるからです。次のlinkを見て下さい。![]() 三角関数の公式覚え方
三角関数の公式覚え方
![]() sin cos tanの覚え方は英語の筆記体の書き順で。sinは筆記体で書く
sin cos tanの覚え方は英語の筆記体の書き順で。sinは筆記体で書く
この比の覚え方と1:2:ルート3を使う問題が下の方にあります。
sin cos tanの表180°まで
大学受験をする人は覚える事が沢山あるので、sin cos tanの表を覚えるのは時間の無駄です。この表の覚え方として、語呂合わせを使うというのも、あるそうですが、360°まで覚えると、この倍になります。この表は覚えないというより、覚えられないでしょう。
| θ | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sinθ | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cosθ | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tanθ | 0 | √3/3 | 1 | √3 | - |
| θ | 90° | 120° | 135° | 150° | 180° |
|---|---|---|---|---|---|
| sinθ | 1 | √3/2 | √2/2 | 1/2 | 0 |
| cosθ | 0 | -1/2 | -√2/2 | -√3/2 | -1 |
| tanθ | - | -√3 | -1 | -√3/3 | 0 |
1:2:ルート3の覚え方
30°,60°の直角三角形の辺の比が、1:2:ルート3になるのは覚えないといけない。正三角形の半分の直角三角形にピタゴラスの定理を当てはめれば、√(22-12)=√3で、簡単に求められます。ここで、生徒が悩むのは、どこが2で、どこがルート3か、見分けがつかない事です。
この覚え方は、1番大きい角(90°)の対辺が一番大きい比(2)、2番目に大きい角(60°)の対辺が2番目に大きい比(ルート3)になる。と、覚えるのが簡単ですが、ベストな方法ではありません。
1:2:ルート3を使う問題
下の図のように1辺がXの正方形と、30°,60°の直角三角形が接している時、Xの値を求めよ。
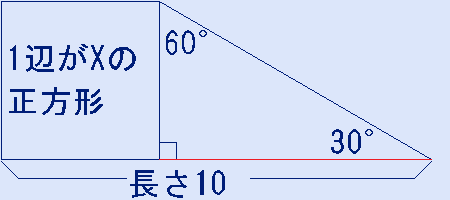
この問題は入試問題ではありませんが、sin cos tanの表を覚えていても、使うのは一部だけです。
1:2:ルート3を使う問題の解答
直角三角形の縦の辺の長さはXだから、直角三角形の横の辺の長さは√3X(赤い線の部分)になります。よって、長さ10=X+√3X。10=(1+√3)X。X=10/(1+√3)。分母を有理化して、X=5(√3-1)。
最後まで読んでいただいて、ありがとうございました。
