因数分解たすき掛けを使わない 応用

1. 因数分解の問題。候補が１種類の場合

   例題：２X^２＋７X＋５…候補が１種類の場合(基礎)

   0. ２X^２がでるためには、答えは（２X＋a）（X＋b）という形になるから、とりあえず、（２X−　）（X−　）と書きます。

      次に空欄の所はかけて「５」になる数ですから、候補は「１、５」か、「５、１」です。（符号はまだ考えない）とりあえず「１、５」から、頭の中で考えます。

   1. （２X−１）（X−５）。（　）を外す事を考えると、１０Xと１Xが出てきますが、（符号はまだ考えない）

      これは足しても引いても７Xにならないから、失格。そこで、

   2. （２X−５）（X−１）と書きます。（　）を外す事を考えると、２Xと５Xが出てきますが、足せば７Xになりますから候補です。

      足して「７」になるように、縦線を入れ、２つの−を＋にして、因数分解の結果は（２X＋５）（X＋１）となります。

2. 因数分解の問題。候補が１種類で、引き算になる場合

   例題：２X^２＋３X−５…候補が１種類で、引き算になる場合

   0. ２X^２がでるために、とりあえず、（２X−　）（X−　）と書きます。

      空欄の所はかけて「５」になる数ですから、候補は「１、５」か、「５、１」です。（符号はまだ考えない）とりあえず「１、５」から、頭の中で考えます。

   1. （２X−１）（X−５）。（　）を外す事を考えると、１０Xと１Xが出てきますが、（符号はまだ考えない）

      これは足しても引いても３Xにならないから、失格。そこで、

   2. （２X−５）（X−１）と書きます。（　）を外す事を考えると、「２X」と「５X」が出てきますが、引けば「３X」になりますから候補です。

      「３X」＝「５X」−「２X」ですから、「＋３X」になるように、縦線を入れ、１つの−を＋にして、因数分解の結果は（２X＋５）（X−１）となります。

3. 因数分解の問題。候補が２種類ある場合

   例題：２X^２＋１５X−８…候補が２種類ある場合。ちょっと難しいかな。

   0. ２X^２がでるために、とりあえず、（２X−　）（X−　）と書きます。

      空欄の所はかけて「８」になる数ですから、候補は「１、８」か　「８、１」か　「２、４」か　「４、２」です。（符号はまだ考えない）とりあえず「１、８」から、頭の中で考えます。

   1. （２X−１）（X−８）。（　）を外す事を考えると、「１６X」と「１X」が出てきますが、（符号はまだ考えない）

      これは引けば「１５X」になりますから、候補です。

      「１５X」＝「１６X」−「１X」ですから、「＋１６X」になるように、縦線を入れ、１つの−を＋にして、因数分解の結果は（２X−１）（X＋８）となります。

      念の為、残りを調べると。

   2. （２X−８）（X−１）の場合。
      （　）を外す事を考えると、８Xと２Xが出てきますが、足しても引いても１５Xにならないので、失格。
   3. （２X−２）（X−４）の場合。
      （　）を外す事を考えると、２Xと８Xが出てきますが、足しても引いても１５Xにならないので、失格。
   4. （２X−４）（X−２）の場合。
      （　）を外す事を考えると、４Xと４Xが出てきますが、足しても引いても１５Xにならないので、失格。

たすき掛けを使う方法

2X²＋3X-5を例に説明します。

たすき掛けを使う場合、以下の４通りを調べないといけませんが、暗算で解くと、消しゴムもノートも節約できます。

1. (2X−5)(1X＋1)
2. (2X＋1)(1X−5)
3. (2X−1)(1X＋5)
4. (2X＋5)(1X−1)

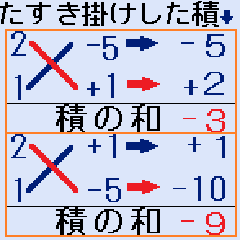
たすき掛けした積の和を計算します。積の和がXの係数＋3になれば、正解です。

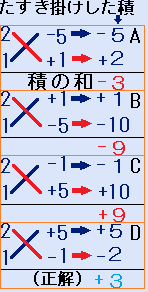
1. 積の和=2×(＋1)＋(−5)×1=−3(だめ)
2. 積の和=2×(−5)＋(＋1)×1=−9(だめ)
3. 積の和=2×(＋5)＋(−1)×1=＋9(だめ)
4. 積の和=2×(−1)＋(＋5)×1=＋3(正解)

たすき掛けを使わない方法

1. 2X²＋3X-5。X²の係数が２なので、とりあえず(2X− )(X− )と書く。確定している所だけを書きます。＋はまだ不確定。
2. 空欄は、A「1　5」かB「5　1」。（符号はまだ考えない）
   • (2X−1)(X−5)。(　)を外すと10Xと1Xが出る。10Xと1Xは、足しても引いても＋3Xにならないので、終了。
   • (2X−5)(X−1)。(　)を外すと2Xと5Xがでる。2Xと5Xは、引けば＋3Xになるので可能性あり。
3. 5の前の符号を＋にすれば、(2X＋5)(X−1)となり、消しゴムを使わずに暗算で、できました。

因数分解で、たすきがけは使わない（準備）も見てください。

因数分解で、「たすきがけを使わない」を主張するサイト（外部リンク）

• 問題：$2X^2+3X-5$

  1. $2X^2+3X-5$
     $=\frac{\mathrm{<span\; class="RB">1</span>}}{\mathrm{<span\; class="RB">2</span>}}(\mathrm{<span\; class="BB">2</span>}\times 2X^2+\mathrm{<span\; class="BB">2</span>}\times 3X-\mathrm{<span\; class="BB">2</span>}\times 5)$

     $X^2$の係数2を式全体に掛け，さらに、逆数の$\frac{\mathrm{<span\; class="RB">1</span>}}{\mathrm{<span\; class="RB">2</span>}}$を掛けた。

  2. $=\frac{\mathrm{<span\; class="RB">1</span>}}{\mathrm{<span\; class="RB">2</span>}}\{{\mathrm{(2X)}}^2+3\times 2X-10\}$
     $=\frac{\mathrm{<span\; class="RB">1</span>}}{\mathrm{<span\; class="RB">2</span>}}\{A^2+3\times A-10\}$

     　$\mathrm{(2X)}=A$とした。

  3. $=\frac{\mathrm{<span\; class="RB">1</span>}}{\mathrm{<span\; class="RB">2</span>}}(A+5)(A-2)$

     　$A^2$の係数が1なので、たすきがけを使わずに因数分解。

  4. $=\frac{\mathrm{<span\; class="RB">1</span>}}{\mathrm{<span\; class="RB">2</span>}}(\mathrm{2X}+5)(\mathrm{2X}-2)$

     　$A=\mathrm{2X}$に戻した。

  5. $=(\mathrm{2X}+5)(X-1)$

     　$\frac{\mathrm{<span\; class="RB">1</span>}}{\mathrm{<span\; class="RB">2</span>}}$を後半の（　）にかけて、（　）を外した。

  詳しくはシグマ先生の【たすきがけ不要】たすきがけを使わない因数分解【２通りの方法をご紹介】へ(外部リンク)

  $\sum _{i=1}^{11}{\mathrm{lawyer}}_i$

• 因数分解でたすき掛けを使うと思いますが、自分はたすき掛けの方法を覚えていません。なぜなら、使う必要がないからです。使わなければ覚える必要もなく、覚えなければ忘れることもないのです。

  詳しくは【たすき掛け不要論】二次式の因数分解を暗算でするへ(外部リンク)

最後まで読んでいただいて、ありがとうございました。