因数分解で使うたすき掛けの方法

たすき掛けとは

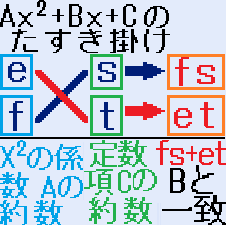例として、AX²+BX+Cをたすき掛けを使い因数分解します。左の図で説明します。

1. eとfには、X²の係数Aの約数を入れます。
2. sとtには、定数項Cの約数を入れます。
3. eとt、fとsをたすき掛けしたfs、etの和=fs+etがXの係数Bと一致すれば完成です。

例題２X^２＋３X－５をたすき掛けで因数分解

X²の項の係数２の正の約数（２と１）と定数項－５の約数（５と１）の組み合わせは、次の４通りです。 (2,1,-1,+5)左上、(2,1,+5,-1)左下、(2,1,-5,+1)右上、(2,1,+1,-5)右下。このうち、Xの係数が＋３になるのは、左下の(2,1,+5,-1)です。

$2X^2$+ 3X－5 = ( 2X+5 ) ( 1X－1 )と因数分解されます。

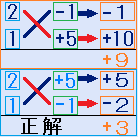
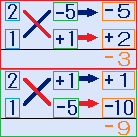
例題の正解の説明

上の図の左下だけが、たすき掛けした結果の+5と-2の和がXの項の係数＋３と等しくなるので、たすき掛けの１行目の２と＋５から（２X+５）、２行目の１と－１から（１X－１）を作ります。

$2X^2+3X－5=($2X+5 ) ( 1X－1 )という因数分解の結果が得られます。

たすき掛けを使わない方法

二次方程式の因数分解で、暗算が得意な人は、たすき掛けを使いません。

上の例題　２X^２＋３X－５の場合ですと、いきなり（２X－　）（X－　）と書き始めます。その後、頭の中で＋５と－１を決めます。因数分解たすき掛けを使わない 応用

最後まで読んでいただいて、ありがとうございました。