二次不等式の解が「全ての実数」「解なし」になる場合

判別式D=0の場合

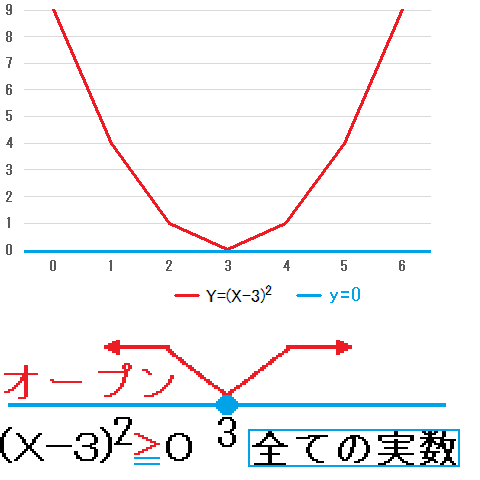
(X-3)²=0の判別式D=0です。左辺の(X-3)²と0の間に、≧、＞、＜、≦を入れた二次不等式の解は、次のとおり、全ての実数、３を除く全ての実数、解なし、X=3となります。Y=(X-3)²のグラフとy=0のグラフの関係を考えれば、はっきりします。

• 全ての実数Xにおいて、Y≧yとなるので、二次不等式(X-3)²≧0の解は、全ての実数となります。
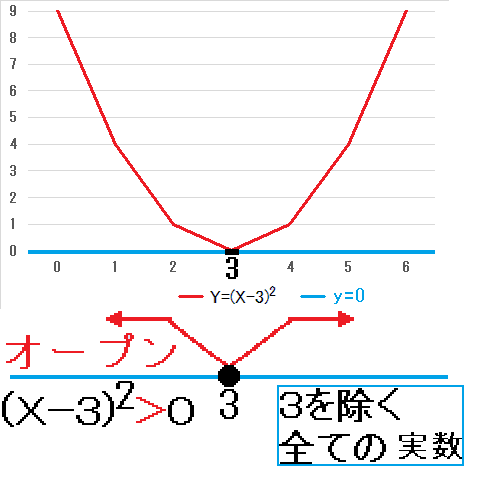• ３を除く全ての実数Xにおいて、Y＞yとなるので、二次不等式(X-3)²＞0の解は、３を除く全ての実数となります。
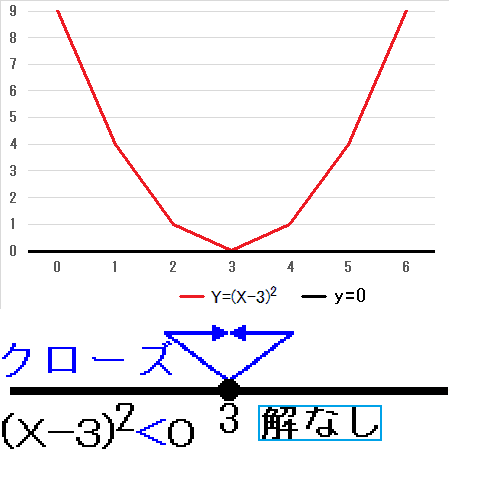• 全ての実数Xにおいて、Y＜yとは、なりませんので、二次不等式(X-3)²＜0の解は、解なし、となります。
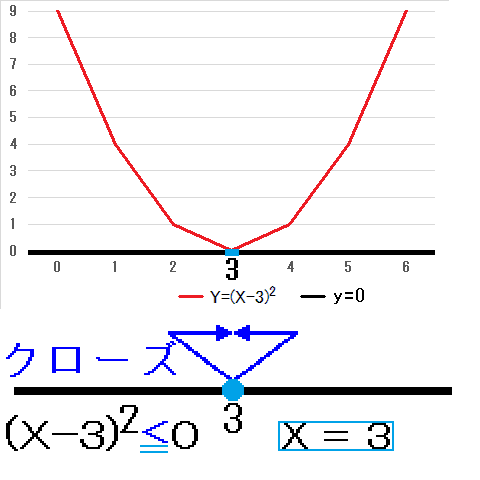• X=3の時だけ、Y＜＝yと、なりますので、二次不等式(X-3)²≦0の解は、X=3、となります。

「全ての実数」「解なし」になる場合は４通り

二次不等式の左辺を因数分解した時、（　）の二乗になる事があります。（Ｘ−３）^２＞０と（Ｘ−３）^２＜０を例にして説明します。

不等号の向きと＝の有無で、次の４つの場合に分類できます。

1. （Ｘ−３）^２＞０。左が開いているオープン。＝が無いから「３」の所は白○。解は、「Ｘは３をのぞく、全ての実数」です。（白○の３をのぞく）
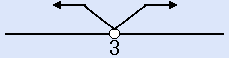
2. （Ｘ−３）^２≧０。左が開いているオープン。＝が有るから「３」の所は黒●。解は、「Ｘは、全ての実数」です。（黒●の３を含める）
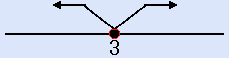
3. （Ｘ−３）^２＜０。左が閉まっているクローズ。＝が無いから「３」の所は白○。解は、「解なし」です。（白○の３をのぞくから）
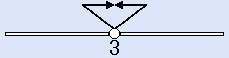
4. （Ｘ−３）^２≦０。左が閉まっているクローズ。＝が有るから「３」の所は黒●。解は、「Ｘ＝３」です。（黒●の３だけを含めるから）

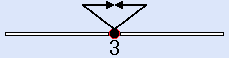
二次不等式のほとんどは、オープンとクローズの解法で、できます。

判別式Ｄ＜０となる場合は、平方完成

判別式Ｄ＜０となる二次不等式の場合は、オープンとクローズで解けません。

二次不等式の問題：Ｘ^２+ａＸ+ｂ＞０をＸ^２+ａＸ+ｂ＝０という二次方程式にかえた時、判別式Ｄ＜０となる場合です。

二次不等式の例題：Ｘ^２−６Ｘ+１１＞０。この時、判別式Ｄ＝３６−４４＝−８、負なので、左辺は有理数の範囲で因数分解できません。

この二次不等式の左辺は、（Ｘ−３）^２+２＞０と平方完成します。平方完成の公式を丸暗記してはダメへ

（Ｘ−３）^２は、どんなＸでも、正または０ですから、（Ｘ−３）^２+２は常に正です。

よって、この二次不等式は、どんなＸでも成り立ちますから、解は「全ての実数」となります。

判別式の負０正と二次不等式の解の関係

「二次不等式の左辺＝０とした時の判別式Ｄの負０正」と、「不等号＞、≧、＜、≦」により場合分けすると、二次不等式の解は以下のようになります。

判別式が負の場合

例：二次不等式の左辺が（Ｘ−３）^２+２の場合、（Ｘ−３）^２+２＝Ｘ^２−６Ｘ+１１＝０とした時の判別式Ｄ＝６²−４×１１＝−８で、負となります。

1. （Ｘ−３）^２+２＞０。解は、「全ての実数」
2. （Ｘ−３）^２+２≧０。解は、「全ての実数」
3. （Ｘ−３）^２+２＜０。解は、「解なし」
4. （Ｘ−３）^２+２≦０。解は、「解なし」

判別式が0の場合

例：二次不等式の左辺が（Ｘ−２）（Ｘ−２）の場合、（Ｘ−２）（Ｘ−２）＝Ｘ^２−４Ｘ+４＝０とした時の判別式Ｄ＝（−４）²−４×４＝０で、０となります。

1. （Ｘ−２）（Ｘ−２）＞０。解は、「Ｘ＝２以外の全ての実数」
2. （Ｘ−２）（Ｘ−２）≧０。解は、「全ての実数」
3. （Ｘ−２）（Ｘ−２）＜０。解は、「解なし」
4. （Ｘ−２）（Ｘ−２）≦０。解は、「Ｘ＝２」

判別式が正の場合

例：二次不等式の左辺が（Ｘ−２）（Ｘ−３）の場合、（Ｘ−２）（Ｘ−３）＝Ｘ^２−５Ｘ+６＝０とした時の判別式Ｄ＝（−５）²−４×６＝＋１で、正となります。

1. （Ｘ−２）（Ｘ−３）＞０。解は、「Ｘ＜２、３＜Ｘ」
   ＞オープン。
   ＝がないのでX=2,X=3は含まれない。
2. （Ｘ−２）（Ｘ−３）≧０。解は、「Ｘ≦２、３≦Ｘ」
   ≧オープン。
   ＝があるのでX=2,X=3も含まれる。
3. （Ｘ−２）（Ｘ−３）＜０。解は、「２＜Ｘ＜３」
   ＜クローズ。
   ＝がないのでX=2,X=3は含まれない。
4. （Ｘ−２）（Ｘ−３）≦０。解は、「２≦Ｘ≦３」
   ≦クローズ。
   ＝があるのでX=2,X=3も含まれる。

最後まで読んでいただいて、ありがとうございました。