|
天武天皇の年齢研究 -目次- -拡大編- -メモ(資料編)- -本の紹介-詳細はクリック 2018年に第三段 「神武天皇の年齢研究」 2015年専門誌に投稿 『歴史研究』4月号 2013年に第二段 「継体大王の年齢研究」 2010年に初の書籍化 「天武天皇の年齢研究」 |
First update
2014/06/20 Last update 2014/11/21 暦法とは暦の定め方です。いつの時代でもその国が定める暦の方法を指します。大まかに、太陽の運行に基づいた暦を太陽暦、月の運行に基づいた暦を太陰暦、そして、古代中国は太陽と月の運行双方を加味した暦として太陰太陽暦を採用しました。 本稿は古代中国の暦法を学び解る範囲で説明を試みながら、日本書紀が採用した元嘉暦と儀鳳暦の違いを明らかにしていきます。そのためにはまず、予備知識が必要です。 正確な測量 古代中国における太陽と月の天文観測の精度は高いものですが、時間測定技術も欠かせません。太陽に対し、始めは棒、後には塔を立て、時間を測定し、その最も影が低くなる冬至(旧暦1月)の日を定め、月に対しては満月から次の満月の中間、月のない日を陰暦、新月の日、朔(さく、ついたち)などと言われた日時を克明に予測していたはずです。問題は太陽、月の動きとは独立した一定速度を測る時間測定が必要になります。
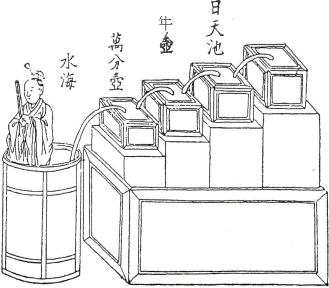
唐の呂才が考案した漏刻『古今塩讐集成』、 漏刻復原模型「水落遺跡」明日香村
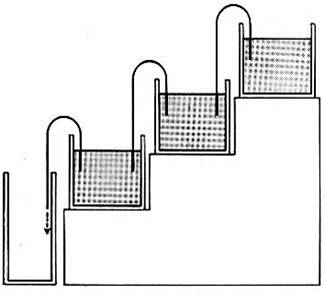
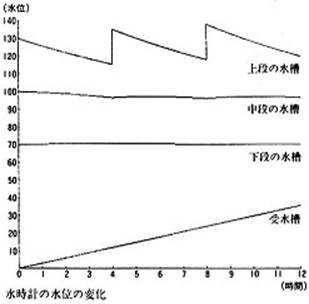
http://www.asukanet.gr.jp/ASUKA4/mizutokei/tokei02.html 漏刻(水時計) 日本書紀によると、「660斉明6年5月、皇太子(中大兄皇子)が初めて漏刻をつくり、人民に時を知らせるようにされた」皇太子、初めて漏尅を造る。民をして時を知らしむ。 「671天智10年4月25日、漏刻を新しい台の上におき、はじめて鐘・鼓を打って時刻を知らせた。 この漏刻は天皇がまだ皇太子であった時(斉明6年)に、始めて自分でお造りになったものであるという、云々。」 夏四月、丁卯朔辛卯、漏尅を新臺に置く。始めて時を打つ。鍾鼓を動す。始めて漏尅を用いる。 此の漏尅は、天皇の皇太子に爲す時に、始めて親ら製造れる所なりと、云々。 どちらにも「初めて」「始めて」と書かれていますが、矛盾ではないでしょう。斉明時の漏刻を中大兄皇太子が初めて作られました。そして、天智10年の漏刻は、始めて鐘・鼓を使用し実用化されたということです。 憶測が許されるなら、この8ヶ月後の12月3日には天智天皇は崩御されますから、この行為は大海人皇子が天智に成り代わって遂行されたとも推測できます。うがった見方ですが、天智10年の新台に漏刻を置いたのが、誰か書かれていません。後に書かれる天武天皇の天文の知識は深く、時刻の計測が重要であることはよくわかっていたはずです。天智天皇に進言し、この頃、自ら体験したものだったと思います。 因みに、この日は太陽暦では6月10日、現在の「時の記念日」です。 最初、上図のような漏刻を見たとき、鐘で一刻ずつ時を知らせるのに、何と大げさな仕組みだろうと思いましたが、これが天文観測に使用されたと考えると納得がいきます。 水時計を説明するために、いろいろなホームページや解説書を探し、上図のように切り貼りしました。 左上は古代唐の呂才が考案した漏刻、『古今塩讐集成』に描かれているものです。上の真ん中は、現在の明日香村に作られた疑似模型です。右上はその目盛りを計る人形です。下の受水槽の水面が上がると、定規の数値が上がり時間が計測できるわけです。 仕組みはおわかりと思います。サイホンでつながった四つの水槽があり、一番上の水槽に定期的に水を入れると、次々水は下に流れ、一番下の人形が据えられた桶に貯まり、浮き輪のついた定規がスライドして、この人形が指すメモリを読むことで、時刻や経過時間が測定できるのです。 測定図面は簡略化された3層になっています。左下のグラフでは一番上の水槽に4時間ごとに水を補給しています。中段、下段の水槽は浸透圧の関係で、大気圧が一定で、水面も一定に維持されます。このような中間槽の数は2段より、模型のように3段にした方が下段に降るほど水面が安定します。最下段の受水槽はどんどん水がたまり、この図では12時間たったところで、一気に排水して、またメモリ0から測定をし直すのでしょう。 古代中国の測定結果、月齢29.530日と下三桁までは現在と誤差がありません。下3桁ですから分刻みの精度が確保されていたことになります。そこまで厳密に計れたか不明ですが、サイホンの仕組みといい、かなり厳密なものと思います。 当時から昼間の日時計と併用して、日々微調整しながら、夜の月や星々の運行を分単位に測定したのです。 太陽と月の公転 一口に、地球や月が一周するという公転という概念にはいろいろな解釈があります。その中で、少なくとも古代中国において、太陽年、朔望月、恒星月の数字はかなりの精度で把握していました。むろん、天動説という概念においてです。以下、「理科年表2013」より書き出しました。 太陽年=365.24219日(地球と太陽と関係) 朔望月=29.530589日(新月から新月) 恒星年=365.25636日(恒星と地球の関係) 恒星月=27.321662日(恒星と月の関係) 近点年=365.25964日(公転の楕円を意識) 近点月=27.554550日(月の楕円周期を意識) 太陽年は地球の歳差運動(地球の地軸がぶれる為、異なる値になる)の影響を加味したもの。 恒星年はある星から見た、地球の動きとなり、比較的正確な地球の公転時間を観測できます。 近点年は、微妙な楕円の公転軌道(ケプラー法則)で、太陽に最も近い点から1周した日数。
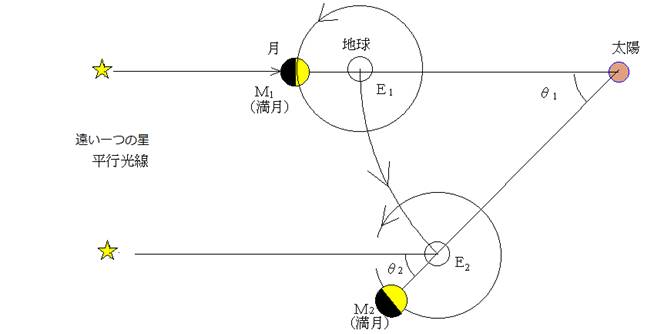
朔望月と恒星月の関係は計算でも求められます。 HPから図をお借りして説明します。http://www.s-yamaga.jp/nanimono/uchu/tsuki-02.htm 単純には、月が地球の周りを一周するには27.32日かかります。これは恒星月と呼ばれ、実際には遠い星の一つを基準に月が同じ位置に戻ってきた時間を測定したものです(M1から一周したM1まで)。 古代で実際に使用されたのは月の満ち欠けでした。しかし、満月から満月までの時間は月が1周すると地球も動いてしまい、1周を超えθ2の分だけすぎてしまいます。満月から満月の日数は 恒星年(ある星から見て太陽の周りを地球が1周する日数)=365.25636日 恒星月(ある星から見て地球の周りを 月が1周する日数)=27.321662日 朔望月(この図では満月から満月までの日数)=T日とすると 月が満月から満月なる地球の移動した割合 θ1=T/365.26日 月が地球の周りを1周し満月に至るまでの割合θ2=(T/27.32日)-1 θ1=θ2なので T/365.26=(T/27.32日)-1 朔望月T=(365.26×27.32)/(365.26-27.32)=29.53日 別解釈から、 1/朔望月=1/恒星月-1/恒星年 の関係式も得られます。 実際には、太陽年、恒星年、朔望月、恒星月も、測定値です。 なお、100年前の太陽年=365.24220日(1900年)でした。昔は現在より公転スピードは遅いという記事があり、計算してみましたが、これから話す3000年程度昔では誤差範囲内で影響はありません。 現在の太陽暦 地球は太陽の周りを 365.2422日(太陽年)で1周し、 月は地球の周りをおよそ29.53059日(朔望月)で1周します。 また、現代の太陽暦は誰もが知るように、大まかに言って、一年365日を12ヶ月に別け、7ヶ月が31日、4ヶ月が30日、1ヶ月が28日で、4年に一度の閏年、2月28日が29日になる月があるというものです。合計4年間では1461日です。よって、平均1年は365.25日です。 365×3年+366×1年=1461日 1461日÷4年=365.25日/年 これは、古代中国の四分暦やユリウス暦と同じといえます。(1行追記2014/11/21) 因みに、大元のグレゴリオ暦は、400年間に97回の閏日を設けるように決められています。 365日×400年+97日=146097日 146097÷400 =365.2425日 古代中国の暦法 今までの、予備知識に基づき、古代中国に目を移します。 中国古暦には黄帝暦より始まるとされ、六種類(黄帝暦、夏暦、殷暦、周暦、魯暦、顓頊暦〔秦〕)があったと伝わります。省略します。 実際に地球が太陽の周りを1周するには 365.24220 日/月 月の満欠けの周期を 29.530589日/月 暦名 使用西暦 1太陽年 1朔望月 太初暦 BC104~ 85 365+ 385/1539 =365.25016 日 29+ 43/81 =29.530862日 四分暦 85~220 365+ 1/4
=365.25 日 29+ 499/940 =29.530851日 景初暦 237~444 365+ 455/1843 =365.24688 日 29+ 2419/4559 =29.530599日 元嘉暦 445~509 365+ 75/304
=365.24671 日 29+ 399/752 =29.530585日 大明暦 510~589 365+
9589/39491 =365.24281 日 29+
2090/3939 =29.530591日 開皇暦 584~596 365+25063/10296
=365.24342 日 29+96529/181920 =29.530612日 大業暦 597~618 365+10866/42640
=365.25483 日 29+
607/1144 =29.530594日 戊寅元暦 626~664 365+ 2315/9464 =365.24461 日 29+
6901/13006 =29.530601日 麟徳暦 665~728 365+ 328/1340 =365.24477 日 29+
711/1340 =29.530597日 太初暦 秦を倒した前漢の太初暦はBC104太初元年の前年の11月1日(朔日)が甲子の午前0時を以て朔の時刻と冬至の時刻が一致するとしました。後漢のAD85章帝元和2年まで190年間使用されました。 19年間に7回の閏月(13ヶ月/年)を設けました。これは上記古来続く暦法の基礎です。また、立春正月を年始とすること、中気のない月を閏月とする歳中閏月法が採用され、その後の暦法に影響を与えました。なお当時は、まだ小数点の考え方はありません。分数になります。 太陽年=365+385/1539=562120/1539=365.2501624日/年 19年=(12×19+7)=235ヶ月なので 朔望月=(562120/1539)×19/235=29+43/81=2392/81=29.530862日/月 ちなみに、分母「81」は音律の基準、竹管81寸に基づくのだそうです。 四分暦 後漢王朝になると、85元和2年から220延康1年までの136年間。現在と同じ一年間=365日+1/4日となります。四分暦と呼ばれる由来です。精度も上がりました。 この後漢の四分暦は古来より続いていた六古暦に基づいて作られたと言われます。BC161後元6年の前年11月1日朔日が甲子の午前0時を以て朔と冬至の時刻が一致する時と定められました。 「四分暦」は、詳細に後漢書の律歴志に説明され、現代に伝わりました。これがその後の中国暦法の大元になったと考えていいようです。 それまでの六種類の古暦同士の暦の大きな違いは、計算の基点、すなわち暦元の取り方が異なり、新たな暦が始まる都度、始まりの干支が変わっていましたが、ここから現在に連なる干支が続くことになります。 後漢王朝の四分暦以降の暦法は、近世清朝(太陽暦)に至るまで、70余りの改変を経たと言われていますが、四分暦の考え方は。ずっと継承され続けたのです。 19年=(12×19+7)=235ヶ月 19年=(365+1/4)×19=6939+3/4日 朔望月=(6939+3/4)÷235=(6939*4+3)/(235*4)=27759/940 =29日+499/940=29.53085106日/月 このように、太陰太陽暦は現代と同じに太陽年と一致し、月の運行も同時に計算しているというすぐれものです。 24節気(にじゅうしせっき) また、1年の日数=365+1/4を12等分した。30+7/16日/月 これを「中」といいます。 その半分が「節」です。(30+7/16)÷2=15+7/32日/月 中と節は年間に交互に12回現れるので、24気と呼ばれました。
しかし、実際の月の運行は29+499/940なので(30+7/16)-(29+499/940)=3409/3760ずれます。 最初の「中」(冬至)と朔(1日)を一致させると、翌月の「中」は朔から3409/3760だけ入った点に移動します。このように月数を次々重ねていくと、「中」が後ろの移動し、最後には「中」がない月が生じます。これを閏月とするのです。 ○1章=19年、としました。 19年間に7回の閏月を設け、これが章法といわれ、後に対峙する考え方が破章法です。 19年単位の考え方ですから、上記のように朔望と季節がそろいます。 ○1蔀=4章=76年 この1章の日数は365+1/4×19=(6939+3/4)日と端数があります。 そこで、4倍にすれば余分な端数が解消されます。 こうして、朔時刻の端数がそろうことになります。76年後のことです。 ○1紀=20蔀=76年×20=1520年(日の干支もそろう) 次に、20蔀にすると日付は60で割り切れます。 365.25×4×20/60=487回目/60干支日 十干十二支(60干支)は60日ごとに繰り返されます。 冬至を甲子日と基点にすると80年目にまた、487回目の冬至が訪れ、甲子日に戻るのです。 ○1元=3紀=60蔀=4560年(年の干支もそろう) 毎年の干支も1紀を3倍にすれば、60年ごとに繰り返され、60蔀は初年の干支年と一致するのです。 この時から、占星術にとって大切な60年干支の考え方も吸収できた優秀な暦法の地位を得たのです。木星の運行にも関係なく、そのたびに調整することがなくなりました。 こうして、四分暦以降、暦が変更されても、60年干支は基点を改める必要がなくなり、これ以降、変更されることなく無条件に60日、60年が繰り返されることになりました。現在まで続けられていると言えるものです。 景初暦 後漢が終わり、魏の楊偉によって作られた暦法。19年7閏月(=235ヶ月)の章法を継承します。 魏で237景初1年~西晋~南宋で444元嘉21年まで使われました。 また、北魏でも398天興1年~451正平1年まで使われました。 1太陽年=365+455/1843=365.24688日 1朔望月=(365+455/1843)×19/235 =
29+2419/4559=29.530599日 もう一つ1近点月=27+2528/4559=27.554508日(現行の近点月=27.554550日) すなわち、星と月との関係周期も求めており、この計算が暦に取り入れられ、日月食の開始時刻などを推算できる方法が確立したと言われます。 元嘉暦 宋の天文学者、何承天が編纂した暦法。南朝の宋・斉・梁で、445元嘉22年から509天監8年までの65年間使われました。実測値を重視し、実際の冬至より3日もずれていることを指摘し、天体観測をやり直しています。四分暦と同じで19年に7閏月を置き、厳密に測定した結果、1太陽年は365日は四分暦の端数1/4に対してさらに1/76短いことを突き止めたようです。 1太陽年=365+(1/4)×(75/76)=365+75/304=111035/304=365.24671日 1朔望月は四分暦と同様、19年=(12×19+7)=235ヶ月なので、 19年=(365+75/304)×19=(365x304+75)x19/304日 1朔望月=(365x304+75)x19/(304*235)=111035*19/(19*16*47*5) =22207/752=29日+ 399/752=29.530585日/月 また、元嘉暦では各月を決定する際に、1月中気の「雨水」を基準としました。雨水を先ず決定し、それに単純に暦法上の1太陽年の24分の1ずつ加算していくことによって二十四節気を割り当て、各月を決定するものです。 一度正月の朔を決めてそれに暦法上の1朔望月ずつ加えたものを次の月の朔として繰り返されます。 このため、実際の暦と月の満ち欠けには多少の差異が残ります。これには何承天も気付いており、朔日の決定に月の遅速を考慮した定朔法を用いようとしましたが、採用されなかったとあります。 それまでは、ずれてきていた暦元の位置を3/4日や1日など種々に繰り上げして調整していたものを、さらに徹底した実測により、朔元日冬至の日時を正確に定めました。19年周期ごとに実測により新たに制定すること、304年(76×4)ごとに1年を減じると定め、朔の位置が実際と離れるのを防いだものですが、65年間で次の暦法に変わりました。 大明暦 劉宋の祖沖之によって編纂されました。梁の510天監9年から陳の末年、589禎明3年まで80年間使用されました。古代の歴代暦法のなかでは、この大明暦が一番高い精度を持ちます。 通例、19年に7回の閏月を設ける古い章法を391年に144回の閏月を設け精度を向上させました。 19×20+11=391年に7×20+4=144ヶ月の閏月を設ける。 391年 =(391×12+144) =4836ヶ月 1太陽年 =365+9589/39491=365.24281日(現在365.24220 日/月) 1朔望月 =(365+9589/39491)×391/4836 =29+ 2090/3939 =29.530591日(現在 29.530589日/月) その後の暦法は、計算式がどんどん複雑化していきましたが、精度自身は上がっていません。当時として天文精度の最大値といえます。天文観測と時間測定の精度限界だったようです。 開皇暦 隋が中国を統一。584開皇4年正月に開皇暦が配布されました。596開皇16年まで。南朝の元嘉暦を少し改良した程度のものといわれます。北朝の破章法を採用せず、19年7閏月(=235ヶ月)の章法にしたため、日食予報に失敗し廃されました。 大業暦 隋の597開皇17年から隋の末年618大業14年まで。開皇暦を批判して作られましたが、うまくいかなかったようです。さらに皇極暦に変わりますが、施行することなく、隋は滅亡します。 戊寅元暦 戊寅元暦は唐代初年618年が戊寅、これを記念した呼び名です。626武徳9年から664麟徳1年まで。前戊寅元暦から平朔法から定朔法に変わりました。さらに閏月が精密になっていき、 677年間に249回の閏月を置きます。しかし、精度としては、大明暦におよびませんでした。 677年=19×35+11、249回=7×35+4 1年 =365+ 2315/9464 =365.24461 日 朔望月= 29+ 6901/13006 = 29.530601日 麟徳暦(儀鳳暦) 唐の665麟徳2年~728開化16年、唐の李淳風作。精度としては、前、戊寅元暦とそう変わりません。インドの天文学者、瞿曇羅の用いた経緯暦を採り入れ、複雑過ぎる閏月配置の周期を廃しています。定朔法を用いて、進朔を初めて採用しました。 麟徳暦では、1日を1340分に分け、1年を489428分としていますから、 1太陽年を489428/1340 =365.24477日 朔望月を
39571/1340 =29.530597日 上の公式で太陽年と朔望月の端数の分母を「総法」として「1340」と揃えています。暦の循環する基準となる分母数です。 二十四節気の目的は、旧来12朔望月と1太陽年とのずれを補うための閏月の挿入タイミングの決定するためでしたが、これをやめ、対局に定朔法を採用しました。 定朔法 古代中国の暦法には、平朔法が支配的でした。一方、麟徳暦は定朔法を用いました。ただし、残念ながら太陽と月の運動の遅速をどのように計算したのかの資料は現存していないそうです。 定朔法は、太陽の運行と月の運行の不均等性を考慮し、朔日を必ず1日にしようとする方法です。これにより、日食や月食の予測がより正確にできるようになるからです。 対する古い平朔法では、日月の運行の遅速は考慮に入れられていません。このため、真の朔を含む日が29日、30日や2日になることもあります。その為、儀鳳暦には定朔が導入されたのです。しかし、日本では定朔を用いず、古い平朔法を用いまま計算されています。 麟徳暦と儀鳳暦 儀鳳暦と麟徳暦は同類とよくいわれます。中国の麟徳暦と日本書紀に使われた(儀鳳)暦は違います。1太陽年、1朔望月の結果数字は利用していますが、そのなかの定朔法を使用していません。定朔法の使用は日食、月食予測に関わります。よって、日本の日食的中率は唐や新羅に比較して極端に低いのです。参照:「古代日本の暦法」 麟徳暦は麟徳665麟徳2年に定められ麟徳暦といわれました。これを、新羅は674文武14年春正月に唐から持ち帰り、新暦法とします(三国史記)。 唐の「儀鳳」とは高宗李治の治世(676~679)、日本では天武5~8年です。新羅のように唐の冊封体制内にない日本はこの技術を新羅から情報を得たと思われます。儀鳳暦は日本だけで通用する名前です。新羅で改変されたとも言われますが、それは日本書紀に基づく憶測であり、当時の冊封体制内にある新羅の情勢からは考えにくい説です。月朔干支が書かれた独特の日本書紀の記述ように、新羅の史書は書かれておらず、判断ができないのです。 一方、小川清彦の論文の要約書に、儀鳳暦使用に際して「手間をはぶくために、より簡単な経朔法(定朔法のこと)を採用」したとありますが、こうした憶測を交え小川氏の意見とするのは困ります。 いろいろな可能性が考えられます。確かに、当時日本が定朔法を理解できなかったとも考えられますし、新羅も定朔法を理解できていなかったかもしれません。本稿の考えるように、新羅が定朔法を同じ冊封体制にない日本にそのまま伝えなかったとも考えることもできるのです。 その後、続日本紀、文武天皇の時代になっても、例えば、日本で使用された儀鳳暦は古い平朔のままで、また、進朔という手法、計算で求めた朔の時刻が午後6時を過ぎたら翌日に朔日に進めるという手法を用いていません。麟徳暦と儀鳳暦から算出される、結果数字や干支の類似とは別に、異なるものだと考えた方がいいように思います。 西洋と東洋における暦法の相違 以上、本稿で理解できる限りを書き記しました。 これまでの方法は、紀元前5世紀、古代ギリシャのメトン周期とほぼ同一のため、東から伝わったと言われることがあります。たぶんそれで間違いないと思います。しかし、これだけの微細な方法を熟知することは、すでに、これを理解できる文化が中国に根付いていたということです。さらに、太陽、月の運行のみならず、60年干支、太歳周期など古代中国独特の暦法を結びつけ、知識が積み上がっていく姿は半端ではありません。 考えてみると、仏教も元はインドから伝わった宗教です。外からの文化を貪欲に吸収し、独自に発展させる能力のある国であったと思います。 参考文献 理科年表 平成26年度卓上版 国立天文台編 丸善 2013 山田英雄「即位前紀と大歳記事」『日本書紀』教育社歴史新書<日本史>19、教育社1979年 有坂隆道「古代の歴史」『図解検証現像日本④』旺文社1988 有坂隆道「古代史を解く鍵」講談社学術文庫1999 飯島忠夫「天文暦法と陰陽五行説」『飯島忠夫著作集4』第一書房S55 内田正男編「日本暦日原典第四版」雄山閣出版H4 小川清彦「日本書紀の暦日に就いて」『小川清彦作品集』皓星社1997 ©2006- Masayuki Kamiya All right reserved. |