絶対値を2つ含む方程式の問題と解き方

絶対値を2つ含む方程式 絶対値=絶対値 |X-3|=|X|

問題 $\left|x-3\right|=\left|x\right|$。

X-3、Xの正負はXの値が0と3で変化しますから、X＜0、0≦X＜3、3≦Xの3つの場合に分けます。

1. X＜0の場合

   X-3＜0だから、|X-3|=-X+3。X＜0だから。|X|=-X。よって、-X+3=-Xとなります。これを解けば、+3=0という事になり、解なし。

2. 0≦X＜3の場合

   X-3＜0だから、|X-3|=-X+3。X≧0だから。|X|=X。よって、-X+3=Xとなります。これを解けば、+3=2Xという事になり、X=3/2。これは条件を満足します。(/は割るの意味)

3. 3≦Xの場合

   X-3＞0だから、|X-3|=(X-3)。X≧0だから。|X|=X。よって、X-3=Xとなります。これを解けば、-3=0という事になり、解なし。

4. 1.2.3より答はX=3/2。

|X-3|=|X|をグラフで解く

Y=|X-3|のグラフとY=|X|のグラフの交点のX座標は、|X-3|=|X|の解と一致します。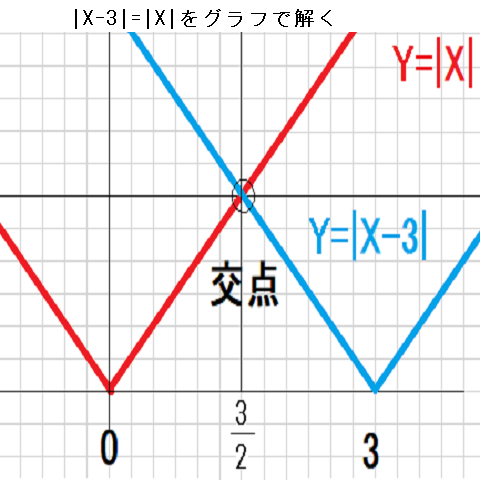

絶対値を1つ含む方程式

絶対値が1つの場合は、絶対値||を外すと±がつくで、できてしまいます。

絶対値を1つ含む方程式 |X|=3

問題 |X|=3。答　X=±3。答はあっていますが、絶対値を外すと±がつくと、覚えるのは危ないです。正しい考え方は、絶対値の中が正か負かで場合分けします。

1. (条件 X≧0の場合)｜X｜=+X なので、X= 3。（この解は条件を満足する）
2. (条件 X＜0の場合)｜X｜=-X なので、-X=3。つまり、X=-3。（この解は条件を満足する）
3. 1.2.は条件を満足するので、答はX=+3,-3。

絶対値の外し方の基本は場合分け

絶対値を1つ含む方程式 |X-3|=5

問題 |X-3|=5。X-3=±5。-3を移行して、X=3±5。答　X=8,-2。答はあっていますが。正しい考え方は

1. (条件 X-3≧0、つまりX≧3の場合)｜X-3｜=X-3 なので、X-3=5。X=8。
2. (条件 X-3＜0、つまりX＜3の場合)｜X-3｜=-(X-3) なので、-(X-3)=5。X=-2。
3. 1.2.は条件を満足するので、答はX=8,-2。

最後まで読んでいただいて、ありがとうございました。