平方完成の公式を丸暗記してはダメ。解の公式の導出・証明が重要

２次関数の平方完成のやり方

平方完成は２次関数のグラフの頂点の座標を求める時にも使います。
y-b=(x-a)²の頂点の座標は(a,b)でスッキリ
二次関数の頂点の座標は平方完成で

２次関数の平方完成の基本例題

ｙ＝X²＋６X＋５を
ｙ＝（X＋Ａ）²＋Ｂのように変形するにはどうしたら、よいでしょうか。
（X＋Ａ）²の（　）を展開するとX²＋２ＡX＋Ａ²となります。 X²＋６X＋５と比較すれば、
Ａ＝３とすれば良い事がわかります。つまり、
Xの係数の半分ですが、これを丸暗記してはいけません。

ｙ＝X²＋６X＋５を変形すると
ｙ＝（X＋３）²＋５。これで良いでしょうか。

ｙ＝（X＋３）²＋５の（　）を展開すると、
ｙ＝X²＋６X＋９＋５となります。
９が余計ですね。余計な９を引いて
ｙ＝（X＋３）²＋５－９
ｙ＝（X＋３）²－４。これで正解。頂点の座標は（－３、－４）となります。

この時、－４は－４のままなのに、＋３が－３になるのは気持ち悪いですよね。だからy-b=(x-a)²の頂点の座標は(a,b)でスッキリ

２次関数の平方完成の例題

ｙ＝X²＋８X＋５を平方完成して、頂点の座標を求めなさい。

1. Xの係数８の半分は４ですから、とりあえず、ｙ＝（X＋４）²と書きます。
2. （　）を展開すると余計な１６が出てきます。そこで、ｙ＝（X＋４）²－１６と書きます。
3. 元々あった＋５を加えて
   ｙ＝（X＋４）²－１６＋５
   ｙ＝（X＋４）²－１１。頂点の座標は（－４、－１１）となります。

X²の係数が1でない問題

ｙ＝３X²＋８X＋５を平方完成して、頂点の座標を求めなさい。右辺の２つの項から３をくくりだして、
ｙ＝３{X²＋８/３X}＋５ (8/3は3分の8の意味)
下線のついたカッコの中の部分だけをさっきと同じように変形します。
ｙ＝３{(X＋４/３)²－１６/９}＋５
３に分配法則を適用。
ｙ＝３(X＋４/３)²－３×１６/９＋５
ｙ＝３(X＋４/３)²－１/３
頂点の座標は(－４/３、－１/３)となります。

平方完成による解の公式の導出・証明

解の公式の導出の練習です。

X²の係数が１で、Xの係数が偶数の場合

X²＋2bX＋c＝0。平方完成すると
（X＋b）²－b²＋c＝0。移項して
（X＋b）²＝b²－c
（X＋b）＝±√(b²－c)
　X＝－ｂ±√(b²－c)
（Xの係数が偶数の時の解の公式。計算は少し楽ですが、似ている公式を覚えようとすると、混同します）

解の公式の導出・証明。X²の係数がaの場合

a＞0という条件で 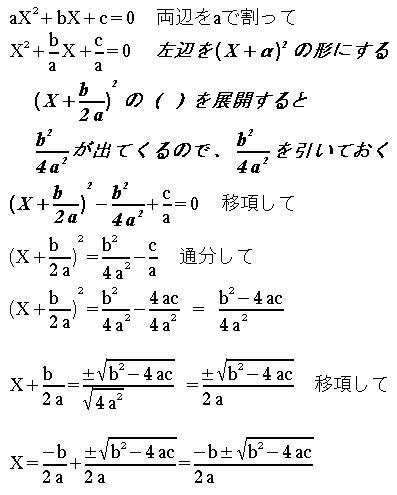↑二次方程式の解の公式です。
ページトップに戻る

最後まで読んでいただいて、ありがとうございました。