11の倍数の見分け方 足す方法と引く方法

２桁ずつ区切り、足す方法

各位を下から２桁ずつ区切り、２桁の数の和が、11の倍数かどうかで判定します。

11の倍数の例：172304。17＿23＿04と２桁ずつ区切る。２桁の数の和=17+23+04=44=11×4なので、元の数172304は11の倍数です。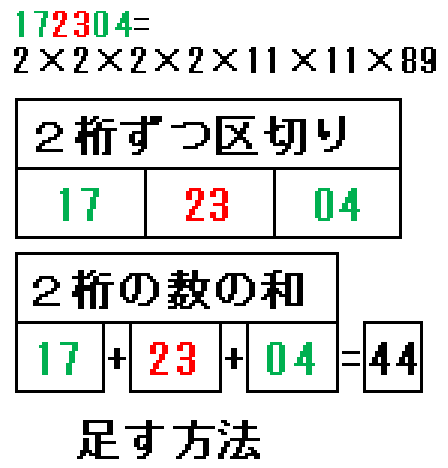

１桁ずつ区切り、引く方法

各位を下から1桁ずつ区切り、下から奇数桁目の数の和と偶数桁目の数の和。この二つの和の差が、11の倍数かどうかで判定します(0は11の倍数)。

11の倍数の例：172304。１７２３０４と１桁ずつ区切る。奇数桁目の数の和7+3+4－偶数桁目の数の和1+2+0=14-3=11なので、元の数172304は11の倍数です。

ジュニア数学オリンピック(中学3年生以下)に出る11の倍数の問題

まず簡単な問題。3桁の数字【□３５】の□に0～9の数字を入れて、11の倍数にするには、何を入れたら良いでしょう。足す方法でやると、□+35が11の倍数になればよいので、答=9です。

ジュニア数学オリンピックに、この方法を知らないとできない問題があります。問題の例。6桁の数字、【３１４□１５】の□に0～9の数字を入れて、11の倍数にするには、何を入れたら良いでしょう。引く方法で解きます。

ジュニア数学オリンピックの問題を引く方法で解く

【３１４□１５】。□に入る数字をＸとします。引く方法：偶数桁目の数の和－奇数桁目の数の和＝（３+４+１）－（１+Ｘ+５）＝２－Ｘ。０≦Ｘ≦９ですから、－７≦２－Ｘ≦２。これが１１の倍数になるので、２－Ｘ＝0。答 Ｘ＝２。0は11の倍数です。

足す方法と引く方法の補足説明

6桁の例だと長くなるので、4桁の例で証明します。

足す方法の簡単な説明

4桁の例：１９１４の場合。１９１４を１９と１４に区切る。１９＋１４＝３３＝３×１１なので、１９１４は11の倍数。

足す方法の厳密ではない証明

１９１４
＝１９×１００＋１４
＝１９×(９９＋１)＋１４ カッコを外す
＝１９×９９＋１９＋１４

(１９×９９)も(１９＋１４)も11の倍数だから、全体も11の倍数。

足す方法のやや厳密な証明

４桁の整数の千の位の数をa、百の位の数をb、十の位の数をc、一の位の数をdとする。

abcd
=a×1000+b×100+(c×10+d)
=100×(a×10+b)+(c×10+d)
=(99+1)×(a×10+b)+(c×10+d)
＝99×(a×10+b)+(a×10+b)+(c×10+d)

９９×(a×１０＋b)は11の倍数だから、(a×１０＋b)＋(c×１０＋d)も11の倍数ならば、元のabcdは11の倍数。

引く方法の簡単な説明

例：１９４７の場合。奇数桁目の数の和＝７＋９＝１６。偶数桁目の数の和＝４＋１＝５。二つの和の差＝１６－５＝１１なので、１９４７は11の倍数。

引く方法のやや厳密な証明

４桁の整数の千の位の数をa、百の位の数をb、十の位の数をc、一の位の数をdとする。

abcd
=1000a+100b+10c+d
=10×(100a+c)+100b+d
=(11-1)×(100a+c)+99b+b+d
=11×(100a+c)-(100a+c)+99b+b+d
=11×(100a+c)-(99a+a+c)+99b+b+d
=11(100a+c)-99a-(a+c)+99b+b+d
=11(100a+c)-99a+99b-(a+c)+(b+d)

１１(１００a＋c)、９９a、９９bは11の倍数だから、－(a＋c)＋(b＋d)も11の倍数ならば、元のabcdは11の倍数。

911テロ 2001年9月11日8時46分は11の倍数

2001911846の素因数分解を筆算で行なうと、以下の画像のようになり、2001911846が11の倍数である事が判ります。2001911846＝11×11×11×752033×2。(752033はソフィー・ジェルマン素数)

この筆算は、2001911846が11の倍数である事が判っていれば思いつきます。どうしたら、2001911846が11の倍数だと見分ける事ができるでしょう。

2001911846が11の倍数だと見分ける方法

足す方法では、2001911846を20_01_91_18_46と二桁ずつ区切り、20+01+91+18+46=176=11×16となり、11の倍数です。

引く方法では、2001911846の奇数桁目の数の和(=0+1+1+8+6=16)－偶数桁目の数の和(=2+0+9+1+4=16)=16－16=0となり、11の倍数です。

911テロと2001911846以外の11の倍数

アメリカ同時多発テロ事件のアメリカン航空11便wikiには、11の倍数がいくつか出てきます。例えば、「アメリカン航空11便は乗員11名を乗せて、WTCのツインタワー北棟(110階建)に突入し爆発炎上」と、11の倍数が３つ出てきます。また、2001911846は11で３回割れます。911テロには、11の倍数が絡むという都市伝説です。911テロ2001年9月11日8時46分は11の倍数

愛＞恋＞好きの物語(全編28中の23話)

「2001年9月11日8時46分に重大な意味があるとしたら、最後の752033にはどういう意味があるの？」

驚いた事に、みほも紙の上で計算をしていた。「本当に不思議ね。でも結局、『それが私達とどういう関係があるの。』という意見は正しいと思うわ。みんな、それぞれ別々の人生を歩いているんですもの。」

「さっきの話、11の倍数には、ある特別な性質があって、それを使えば、簡単にわかる事なんだ。」「雅夫君は数学が得意ね。それも大切な事だわ。」 「でも、数学では世界を救えない。だよね。」「そんな事はないと思うわ。世の中、単純じゃないから。」 「わかった。数学だけでは世界を救えない。数学で世界の一部を救う事はできる。」「たぶん、そんなところだと思うわ。世界が『平和で幸せな所になる』の特効薬はあると思う？」 「ん～。あるかもしれないけど、思いつかないね。」「未来はわからないわ。だから、やれる事はやってみる。それが大切だと思うの。特効薬はあるかもしれない。でも、何が特効薬かは、わからないわ。」
詳しくは愛＞恋＞好きの物語。911テロと11の倍数23話

最後まで読んでいただいて、ありがとうございました。