三角形の面積の最小値を微分で求める
 質問サイトM君の問題より
質問サイトM君の問題より
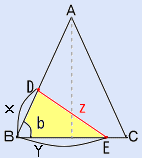
AB=AC=15、BC=10の三角形ABCがある。AB上に点D、BC上に点Eを取り、三角形DBEの面積が三角形ABCの半分であるという条件で、DEの長さZの最小値を求めよ。
最小値を微分で求める為の準備
AとBCの中点を結ぶと直角三角形が2つできる。
その直角三角形で三平方の定理を使えば△ABCの高さ=10√2となる。また、sin b=2√2/3、cos b=1/3となる。
三角形の面積とsinの公式
三角形の面積とsinの公式:S=1/2・b・c・sin Aを使って
与えられた条件の△DBE=1/2・△ABCは、
1/2・X・Y・sin b=1/2・(1/2・10・10√2)となる。
sin b=2√2/3を代入すれば
1/2・X・Y・2√2/3=25√2→XY=75→Y=75/Xとなる。
この条件(XとYについての条件)の基に、Zの値を調べるのだから、余弦定理(XYZが入っている)をとにかく使ってみる。答を出す事に、こだわらないのがコツ。
余弦定理
Z2=X2+Y2-2XY・cos b
(変数を減らす為に、Y=75/Xを使う。)
=X2+(75/X)2-150・1/3
=X2+752/X2-50
Z>0だから、Zの最小値を見つける事とZ2の最小値を見つける事は同値
最大値・最小値を調べる為に、Z2=X2+752/X2-50をXで微分する。
(Z2)’=2X-2・752/X3
(Z2)’=0になるのは、
2X=2・752/X3→X4=752
X>0なので、X=√75=5√3
(Z2)’=2/X3{(X2+75)(X+5√3)(X-5√3)}
X>0なので、(Z2)’の正負は(X-5√3)で決まる。
増減表(最大値・最小値を調べる一般的な方法)
0<X<15に注意。
| X | 0 | 5√3 | 15 | ||
| (Z2)’ | - | 0 | + | ||
| Z2 | ↓ | 最小 | ↑ |
Z2はX=5√3で最小値となる。
Z2=X2+752/X2-50に
X=5√3を代入すれば、Z2=100
よってZの最小値=10
ちなみに、この時、Y=5√3となる。
最後まで読んでいただいて、ありがとうございました。
