因数分解 最低次数で整理する問題

(a－b)3＋(b－c)3＋(c－a)3を因数分解せよ。
()を全部展開し、次数はa,b,cどれも同じなので、aについて整理してから因数分解。

因数分解の問題 解き方

この問題を計算ミスしないで解くには、様々な知識が必要です。その都度のリンク先を参考にして下さい。

3つの( )3の展開

(a－b)3の展開公式を忘れたらパスカルの三角形で展開の公式を導出

与式＝a3－3a2b＋3ab2－b3
　　＋b3－3b2c＋3bc2－c3
　　＋c3－3c2a＋3ca2－a3＝続く

最低次数の文字で整理

最低次数の文字で整理するの意味がわからない時は因数分解の原則 最後は最低次数へ

与式＝a3－3a2b＋3ab2－b3
　　＋b3－3b2c＋3bc2－c3
　　＋c3－3c2a＋3ca2－a3

ここで、a3、b3、c3は±で消えるので、右のようにチェックを入れるのが、計算ミスしないようにする工夫です。

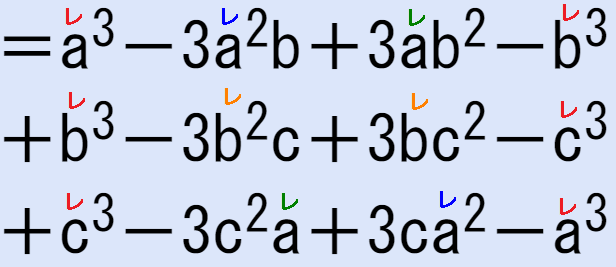さらに数式にチェックを入れる最低次数の文字で整理
この時も、右図のように、チェックを入れていくと、間違えにくい。
(a2がある項)を書き出して、ついでにa2をくくり出し、チェックを入れる。(aがある項)を書き出して、aをくくり出し、チェックを入れる。(aのない項)を書き出して、チェックを入れる。

続く＝｛ a2(－3b＋3c) ｝＋｛ a(3b2－3c2) ｝＋｛ (－3b2c＋3bc2) ｝＝続く2

｛　｝の中を因数分解

3つの｛　｝をそれぞれ因数分解すると、共通因数 3(c－b)が出て来る。
【補足:b2－c2=(b+c)(b－c)=－(b+c)(c－b)】

続く2=｛3a2(c－b)｝＋｛－3a(b+c)(c－b)｝＋｛3bc(c－b) ｝＝続く3

全体を見て因数分解

共通因数 3(c－b)をくくり出して
続く3＝3(c－b)｛a2－(b＋c)a＋bc｝＝続く4

さらに因数分解

a2－(b＋c)a＋bc＝(a－b)(a－c)なので
続く4=3(c-b)(a-b)(a-c)=3(a-b)(b-c)(c-a)

a2-(b+c)a+bc 公式は使わない

a2－(b＋c)a＋bc＝(a－b)(a－c)となりますが、X2＋(a＋b)X＋ab=(X+a)(X+b)の因数分解公式は使いません。

これは、X2＋５X＋６=0を因数分解して解く形のパターン。かけて６、足して５になる２つの数字を見つけるパターンです。因数分解たすき掛けは必要ない

最後まで読んでいただいて、ありがとうございました。