二次不等式の解の安直な覚え方 オープンとクローズ

(Ｘ−３)(Ｘ―４)＞０と(Ｘ−３)(Ｘ―４)＜０の二次不等式の解を考えます。

ここでは、左が開いている不等号＞をオープン。左が閉じている不等号＜をクローズと呼びます。

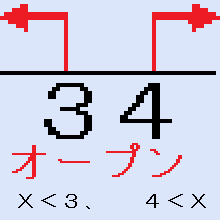  • 二次不等式（Ｘ−３）（Ｘ―４）＞０の解を数直線で表した図 不等号＞の左が開いていてオープンだから、 二次不等式
    （Ｘ−３）（Ｘ―４）＞０の解は、Ｘ＜３、４＜Ｘです。

    Ｘの範囲を数直線で表すと、右の図になります。

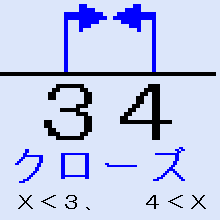  • 二次不等式（Ｘ−３）（Ｘ―４）＜０の解を数直線で表した図不等号＜の左が閉じていてクローズだから、二次不等式
    （Ｘ−３）（Ｘ―４）＜０の解は、３＜Ｘ＜４です。

    Ｘの範囲を数直線で表すと、右の図になります。

二次不等式の不等号「＞オープン」と「＜クローズ」

二次不等式は因数分解して、（　）×（　）(＞か＜)０となります。
不等号は左側（Ｘのある側）が、オープン＞とクローズ＜のどちらかになります。

数直線で二次不等式をあらわした時のオープンとクローズのイメージ

Ｏ.オープン二次不等式の解がオープンの数直線 Ｃ.クローズ二次不等式の解がクローズの数直線

O.とC.のどちらがオープンのイメージですか。Ｏ.ですよね。覚えちゃだめですよ。自分の感覚を信じてください。

数直線で二次不等式をあらわすと。オープン

二次不等式の例題：（Ｘ−３）（Ｘ−４）＞０はＯオープンです。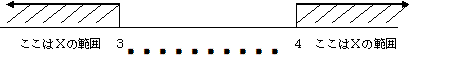二次不等式の解がオープン答（解）はＸ＜３　、　４＜Ｘ

数直線で二次不等式をあらわすと。クローズ

二次不等式の例題：（Ｘ−３）（Ｘ−４）＜０はＣクローズです。二次不等式の解がオープン答（解）は３＜Ｘ＜４

二次不等式の解答の仕方　オープン

二次不等式の答（解）は、[Ｘ＜３、４＜Ｘ]とか、[３＜Ｘ＜４]とかに、なります。
オープンの図をもう一度見てください。
Ｘの範囲　３…４　Ｘの範囲となっています。
数直線は右の方が大きい（＜）。解は、Ｘ＜３、４＜Ｘです。

オープン クローズで解けない二次不等式

二次不等式の問題：Ｘ２+ａＸ+ｂ＞０をＸ２+ａＸ+ｂ＝０という二次方程式にかえた時、判別式Ｄ＜０となる場合は、この方法では解けません。

判別式Ｄ＜０となる場合の解は「全ての実数」「解なし」「Ｘ＝２以外の全ての実数」「Ｘ＝２」等に、なります。 二次不等式の解が「全ての実数」「解なし」になる場合

最後まで読んでいただいて、ありがとうございました。