三次方程式が因数分解できない時は解の候補を1つ見つけて
三次方程式は因数分解の公式を使ってと因数分解できます。
しかし、 は公式が使えないので、因数分解できません。このを因数分解する手順は以下のとおり。
- 定数項(-4)の約数をヒントに、の解の候補を見つけます。解の候補は、X=1で、因数定理より、は(X-1)を因数に持ちます。
- を因数(X-1)で割ります。
-
f(x)=X3+X2+2X-4を因数(X-1)で割る
ⅰ解の候補X=1の見つけ方は後述。
 解の候補の見つけ方
解の候補の見つけ方下の図は、三次方程式が因数分解できない時に使う多項式の除法のやり方です。ほとんど、小学校の時に習った割り算の筆算と同じようにするので、組立除法より簡単です。
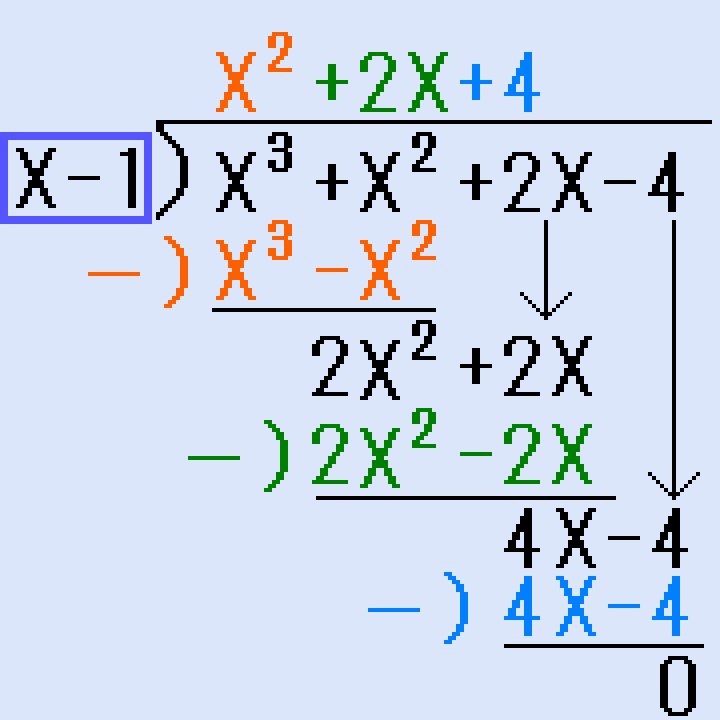 と、因数分解できます。
と、因数分解できます。多項式の除法 筆算でのやり方
多項式(X3+X2+2X-4)を(X-1)で割ります。組立除法は使いません。小学校の時に習った割り算の筆算と同じようにします。
- X3+X2+2X-4の先頭X3とX-1の先頭Xだけを見てX2を立てます。X2とX-1をかけて、X3-X2。引き算して2X2、そして、+2Xを下ろします。
- 2X2+2Xの先頭2X2とX-1の先頭Xだけを見て+2Xを立てます。 +2XとX-1をかけて、2X2―2X。引き算して4X、そして、-4を下ろします。
- 4X-4の先頭4XとX-1の先頭Xだけを見て4を立てます。4とX-1をかけて、4X-4。引き算して0。
と、因数分解できました。
ややこしい感じがしますが、先頭だけを見るという事に注意すれば、小学校の割り算と同じです。組立除法より簡単な理由がここにあります。
小学校の整数の割り算 筆算でのやり方
 これは、小学生のレベルですから、以下の説明を見る必要はないでしょう。前の多項式の除法との関係で書きました。
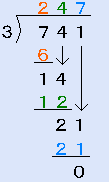
これは、小学生のレベルですから、以下の説明を見る必要はないでしょう。前の多項式の除法との関係で書きました。- 7と3を見て、2を立てます。2と3をかけて、6。引き算し、4を下ろします。
- 14と3を見て、4を立てます。4と3をかけて、12。引き算し、1を下ろします。
- 21と3を見て、7を立てます。7と3をかけて21。引き算し0。
-
解の候補の見つけ方 定数項の約数
三次方程式: X3+……+定数項の整数解(有理数解)が1個あるとすると
と、因数分解されます。
を展開すると、X3+……-aCです。よって、
X3+…+定数項=X3+…-aCとなり、解の候補aは定数項の約数になります。
解の候補と定数項の約数の関係
の係数が1の時
定数項Dの場合、解の候補は定数項Dの約数です。
例:の場合、解の候補は定数項-4の約数、(±1、±2、±4)です。
となるので、解の候補はX=1で、因数定理よりはで割り切れます。
と、因数分解できます。
(参考)の係数が1でない時
定数項Dの場合、解の候補は定数項Dの約数と、それをの係数Aで割ったものです。
例:の場合、解の候補は、定数項 -4の約数(±1、±2、±4)と、それをの係数2で割った です。
となるので、解の候補はX=1で、因数定理よりはで割り切れます。
と、因数分解できます。
三次方程式が因数分解できない時の解法まとめ
定数項を因数分解するには。
- 三次方程式の定数項の約数(d1,d2,d3…とする)を全て上げる。
- が因数分解できるならば、(d1,d2,d3…)の中に最低1個はに代入した時にとなるものがある。それをDとする。
- 因数定理より、はを因数に持つ。
- を因数で割る。多項式の除法。
- は、上記の計算の商との積として因数分解できる。
最後まで読んでいただいて、ありがとうございました。
